Yestok.pl

Opracowanie powstało w oparciu o wersję programu istniejącą w trakcie jego pisania, Libre Office: 5.3.4, Apache OpenOffice: 4.1.3.

Jedną z najczęściej wykorzystywanych funkcji wykorzystywanych w arkuszach kalkulacyjnych jest funkcja JEŻELI. Ta wygodna funkcja zawiera trzy argumenty i ma następującą postać formalną:

=JEŻELI(wyrażenie logiczne;

   formuła,gdy wyrażenie ma wartość PRAWDA;

      formuła,gdy wyrażenie ma wartość FAŁSZ)

Pozwala wprowadzić do komórki arkusza wynik obliczony wg jednej z dwóch podanych formuł, zależnie od tego, czy wyrażenie logiczne będące pierwszym argumentem funkcji ma wartość PRAWDA, czy FAŁSZ.

Przykładowo, jeśli w komórkach kolumny „A” znajdują się liczby odpowiadające pensji, a w kolumnie „B” ma pojawić się dodatek 200 zł tylko wtedy gdy pensja wynosi co najwyżej 1500 zł, to formuła wpisana do komórek kolumny „B” miałaby postać:

	=JEŻELI(An<=1500;200;0)

Zatem gdy w komórce A_n znajduje się liczba 1500 lub mniejsza, to logiczną wartością pierwszego argumentu jest PRAWDA i do odpowiadającej komórki B_n wpisana zostanie wartość 200, gdy liczba w A_n będzie większa od 1500, wartością logiczną tego wyrażenia jest FAŁSZ i do odpowiadającej komórki B_n zostanie wpisane 0.

Ta najprostsza forma tej funkcji jest wykorzystywana najczęściej. Jednakże złożoność procesów obliczeniowych powoduje niekiedy dość znaczne rozbudowanie całego wyrażenia obliczeniowego. Dzieje się tak dlatego, że zgodnie z ogólną definicją funkcji każdy argument funkcji może być zastąpiony kolejną funkcją, która także może mieć swoje argumenty.

Jednym z przykładów, jakie chcę przytoczyć, jest znaleziona na forum internetowym formuła o złożonej budowie wielokrotnie wykorzystującą funkcję JEŻELI.

Formuła wykorzystuje zawartość komórki będącą wynikiem funkcji DZIEŃ.TYG. Funkcja ta ma dwa argumenty. Pierwszy to data, dla której należy wyznaczyć odpowiadający jej dzień tygodnia. Drugi to typ zwracanej wartości. DZIEŃ.TYG zwraca wartość z przedziału od 1 do 7 odpowiadającą odpowiednio dniom tygodnia od niedzieli (1) do soboty (7) (gdy drugi argument jest pominięty lub ma wartość 1) albo od poniedziałku (1) do niedzieli (7) (gdy drugi argument ma wartość 2).

Zbudowana formuła miała w komórce wyświetlić skróty nazw dni tygodnia, czyli „Pn”, gdy 1, „Wt”, gdy 2 itd. Autor formułę zbudował tak:

=JEŻELI(D2=1;"Pn";

   JEŻELI(D2=2;"Wt";

      JEŻELI(D2=3;"Śr";

         JEŻELI(D2=4;"Cz";

            JEŻELI(D2=5;"Pt";

               JEŻELI(D2=6;"So";

                  JEŻELI(D2=7;"Nd";"Wpisz numer dnia w tygodniu")))))))

To nie jest może najbardziej złożona postać, ale i tak nastręcza kłopotów przy pisaniu. Najczęściej dotyczy to właściwie użytych nawiasów i właściwej ich ilości.

Zanim jednak omówię ten problem, nawiążę do opracowania, także znajdującego się w serwisie pod pozycją „Złożone formuły obliczeniowe” (https://yestok.pl/gen/y45.php). Napisałem w nim o kilku problemach związanych z tworzeniem złożonych formuł. Jedną z propozycji jest zmiana koncepcji obliczeń i ta sugestia szczególnie nadaje się do powyższego algorytmu. Tak naprawdę możemy utworzyć gdzieś w arkuszu, np. na nowej karcie, tabelkę poziomą albo pionową, w której pierwszy wiersz (kolumna) będzie zawierać siedem liczb od 1 do 7 a drugi wiersz (kolumna) wpisane odpowiednio skróty nazw od „Pn” do „Nd”. Dla łatwiejszego omówienia problemu przypiszę tej tabelce nazwę, np. „Dni_tygodnia”. Mogę teraz, w odpowiednim miejscu, użyć funkcji WYSZUKAJ.POZIOMO, gdy tabelka jest wierszowa lub WYSZUKAJ.PIONOWO, gdy tabelka jest kolumnowa. Nawiązując do powyższej formuły, można ją zastąpić następująco:

	=WYSZUKAJ.POZIOMO(D2;Dni_tygodnia;2)

Identyczną listę argumentów należałoby wpisać dla wersji dotyczącej tabelki pionowej. Formuły te zwrócą tekst odpowiadający liczbie znajdującej się w komórce D2.

Wspomniałem o tych funkcjach, gdyż one są także często wykorzystywane w sytuacjach, gdy na podstawie jednej ze znalezionych wartości należy zwrócić inną, odpowiadającą tej znalezionej, wartość. O funkcjach arkusza napisałem w opracowaniu „Arkusz kalkulacyjny dla absolutnie zielonych. Cz. 3” zamieszczonym w dziale „Ogólne” serwisu (https://yestok.pl/gen/yak03.php).

Nie jest to jednak jedyna funkcja, którą można wykorzystać, nie jest nawet najprostsza. Wymieniłem ją jednak na pierwszym miejscu, bo jak wspomniałem jest funkcją często używaną.

Warto zauważyć, że liczba określająca dzień tygodnia jest jednocześnie numerem kolejnym komórki tabelki zawierającej odpowiadające teksty.

Można więc zapisać tylko wiersz lub kolumnę z samymi skrótami nazw i traktując ten obszar jak jednowierszową (albo jednokolumnową) macierz, odwołać się do elementu tej macierzy za pomocą funkcji INDEKS.

Takiemu obszarowi, na potrzeby tego przykładu, nadam nazwę (nazwy bardzo ułatwiają tworzenie formuł) – „Macierz” i użyję funkcji: gdy macierz jest pozioma

=INDEKS(Macierz;1;D2)

albo gdy macierz jest pionowa

=INDEKS(Macierz;D2;1)

W tej funkcji pierwszy argument określa macierz, drugi argument wskazuje wiersz macierzy a trzeci kolumnę.

Ponieważ do wyznaczenia numeru dnia tygodnia użyto funkcji DZIEŃ.TYG, to możliwym rezultatem jest zawsze tylko jedna z liczb całkowitych od 1 do 7, nie ma więc możliwości uzyskania liczby wykraczającej poza dopuszczalny zakres. Daty w Calcu są traktowane jak liczba dni, jakie upłynęły od pewnej daty początkowej (w LibreOffice domyślnie jest to 30 grudnia 1899 r,) więc pusta komórka, która powinna zawierać datę jest traktowana jak liczba 0, czyli odpowiada dacie początkowej. Ewentualne liczby ujemne są traktowane jako dni poprzedzające tę początkową datę. Tak więc wartość liczbowa zawsze odpowiada jakiemuś dniu tygodnia.

No dobrze, powie któryś z czytelników, ale ja nie chcę w arkuszu tworzyć żadnych dodatkowych tabelek, i co wtedy?

W takiej sytuacji można skorzystać z elementu, który nazywamy stałą tablicową. Taką stałą zapisuje się w postaci kolejnych wierszy i kolumn, bezpośrednio w formule, obejmując ten zapis nawiasami klamrowymi. Odpowiednikiem formuły pokazanej na powyższym rysunku byłaby wówczas taka:

=INDEKS({"Pn."."Wt."."Śr."."Cz."."Pt."."So."."Nd."};1;C9)

W tej formule stała tablicowa zawiera skróty nazw dni tygodnia jako jeden wiersz. W LibreOffice domyślnym separatorem kolumn w tablicy jest znak kropki, a symbolem końca wiersza i rozpoczęciem następnego jest średnik. W powyższym wzorze zapis w nawiasach klamrowych odpowiada macierzy składającej się z jednego wiersza i siedmiu kolumn. W Apache OpenOffice symbolem oddzielającym kolumny jest średnik a symbolem zakończenia wiersza i rozpoczęcia następnego jest pionowa kreska (na klawiaturze zazwyczaj razem z ukośnikiem odwrotnym).

Wykorzystanie wcześniej wspomnianej funkcji WYSZUKAJ.POZIOMO, mogłoby wyglądać następująco:

=WYSZUKAJ.POZIOMO(C4;{1;2;3;4;5;6;7|
    "Pn.";"Wt.";"Śr.";"Cz.";"Pt.";"So.";"Nd."};2)

Powyższa formuła została zapisana w sposób właściwy dla Apache OpenOffice. Zapis w nawiasach klamrowych odpowiada macierzy złożonej z dwóch wierszy i siedmiu kolumn. Warto ponadto wiedzieć, że jeśli plik zostanie odczytany przez program Calc w alternatywnej wersji, to separatory zostaną automatycznie zamienione na obowiązujące w tej wersji.

Rozdział poświęcony stałym tablicowym znajduje się w opracowaniu „Formuły tablicowe w arkuszach kalkulacyjnych” (https://yestok.pl/gen/y44.php)

To jednak nadal nie są wszystkie rozwiązania. Komórka zawierająca formułę DZIEŃ.TYG odwołuje się przecież do komórki zawierającej datę. A to oznacza, że można w komórce, w której ma pojawić się nazwa dnia tygodnia, umieścić tę datę ponownie i komórce tej nadać odpowiednie formatowanie.

Na powyższej ilustracji widać datę wprowadzoną do komórki D12 i formułę powielającą tę datę w komórce E12. Tyle że tym razem komórce D12 przypisane jest formatowanie użytkownika, powodujące wyświetlenie skróconej nazwy dnia tygodnia odpowiadającej tej dacie, skróty te będą jednak takie, jakie wbudowano do arkusza kalkulacyjnego. Przypomnę, że komórka E12 zawiera nadal wartość liczbową. To sposób przedstawienia tej liczby powoduje, że widać tekst „sob.”. Inaczej mówiąc, gdyby w komórce np. F12 wpisano formułę =E12=”sob.” wynikiem byłby FAŁSZ, gdyż E12 zawiera w rzeczywistości liczbę 42952 odpowiadającą liczbie dni, jakie upłynęły od daty początkowej do 5 sierpnia 2017 roku.

Gdybyśmy jednak chcieli w tej komórce umieścić tekst odpowiadający temu dniu tygodnia, bo np. w innych miejscach arkusza chcemy skorzystać z warunku w postaci =JEŻELI(E12=”sob.”;…) to osiągniemy to, wykorzystując jeszcze inną funkcję: TEKST.

Funkcja ma dwa argumenty, pierwszym jest jakaś wartość liczbowa a drugim format przedstawienia tej wartości, zapisywany w taki sam sposób, w jaki widać to na powyższej ilustracji w polu „Kod formatu”. Wynikiem działania funkcji jest przedstawienie sformatowanej wartości w postaci tekstu. Tak więc, zamiast formatować komórkę E12, można do niej wpisać formułę: =TEKST(D12;”nn”).

Jak zatem widać zmieniając koncepcję obliczeń, można znacznie uprościć tworzone formuły. Wróćmy jednak do zagadnienia, co jeśli rzeczywiście chcemy zrealizować obliczenia za pomocą złożonej funkcji JEŻELI?

Moja sugestia to przygotować sobie najpierw schemat blokowy takiego obliczenia. Pozwoli to na „zobaczenie” czy wszystkie przypadki zostały rozwiązane. Schemat taki proponuję budować z dwóch typów elementów: pierwszy to romb, w schematach blokowych nazywany blokiem decyzyjnym. Wewnątrz wpisywane jest wyrażenie logiczne, jakie należy obliczyć. Pamiętajmy, że wyrażenia logiczne mają tylko dwa możliwe wyniki: PRAWDA lub FAŁSZ.

Linie ze strzałkami wskazują, ścieżkę wyboru działania algorytmu, po jakiej należy podążać w zależności od wyniku działania bloku decyzyjnego. Drugi element to prostokąt, w którym można zapisać żądaną akcję, nazywany też blokiem procesu. Każda z linii może zatem prowadzić do bloku procesu albo do kolejnego bloku decyzyjnego. Z logiki budowy funkcji JEŻELI wynika, że wyrażenie logiczne wpisane wewnątrz rombu odpowiada pierwszemu argumentowi funkcji, wpisywanym po nawiasie otwierającym. Ścieżka wyniku PRAWDA prowadzi do akcji opisanej drugim argumentem, wpisywanym po średniku zaś ścieżka wyniku FAŁSZ prowadzi do akcji opisanej trzecim argumentem i dopiero po tej akcji pojawia się nawias zamykający funkcji.

Zobaczmy zatem taki schemat dla tej złożonej funkcji. Przytoczę ją tutaj po raz drugi.

=JEŻELI(D2=1;"Pn";

   JEŻELI(D2=2;"Wt";

      JEŻELI(D2=3;"Śr";

         JEŻELI(D2=4;"Cz";

            JEŻELI(D2=5;"Pt";

               JEŻELI(D2=6;"So";

                  JEŻELI(D2=7;"Nd";"Wpisz numer dnia w tygodniu")))))))

Schemat ten odbiega od przytoczonej formuły i kończy się na przedostatnim użyciu funkcji JEŻELI. Jeśli bowiem wartość w D1 nie jest liczbą 6, to musi być liczbą 7, czyli odpowiadać niedzieli i nie ma potrzeby badać czy to jest 7. Powyżej wyjaśniałem, że funkcja DZIEŃ.TYG nie zwróci innej wartości niż jedną z tych liczb. Pomijam oczywiście wartości sygnalizujące błąd.

Przyglądając się schematowi widać, że obejmuje on wszystkie możliwe działania wynikające z relacji. Widać także, że każda ścieżka FAŁSZ w tym schemacie, z wyjątkiem ostatniej, prowadzi do następnej funkcję JEŻELI, a to oznacza, że nawiasy zamykające pojawią się dopiero po ostatniej akcji w ścieżce FAŁSZ i będzie ich tyle, ile takich ścieżek wystąpiło.

Ten sam autor w innym miejscu arkusza utworzył inną formułę, tym razem skarżąc się, że nie działa ona prawidłowo. Jest to złożona formuła, ale nawet nie wiedząc, co ona oblicza, możemy stwierdzić, że nie jest dobrze napisana. Oto ona a poniżej schemat narysowany na jej podstawie;

=JEŻELI(D2=6;
   JEŻELI(E2<=6;E2;
      JEŻELI(E2>6;6;
         JEŻELI(D2=7;0;
            JEŻELI(D2=1;
               JEŻELI(E2<=9,5;E2;
                  JEŻELI(E2>9,5;9,5)))))))

Jak widać, trzy relacje występujące w tej formule nie mają przypisanej akcji alternatywnej, czyli nie wystąpił dla nich trzeci argument funkcji JEŻELI a to oznacza, że wyniki mogą być niepoprawne. Program Calc reaguje na brak argumentu w zależności od tego, czy jest to wersja LibreOffice, czy Apache OpenOffice.

LibreOffice Calc pozwala na pominięcie każdego z argumentów i przyjmuje wówczas, że ten pominięty argument odpowiada wartości 0. Teoretycznie można więc wpisać funkcję JEŻELI w postaci =JEŻELI(;;) co spowoduje wstawienie liczby 0 do komórki z taką formułą. 0 dlatego, że pominięcie pierwszego argumentu jest traktowane jak 0, a zero odpowiada wartości FAŁSZ, co dla tej funkcji oznacza wybór trzeciego argumentu, który jeśli go brakuje, zostanie zastąpiony zerem.

Inaczej jest w Apache OpenOffice. Ten dopuszcza pominięcie tylko ostatniego argumentu, wstawiając jako jego wynik stałą FAŁSZ, czyli w arytmetycznym zrozumieniu tej wartości – 0. Jeśli zostanie pominięty drugi argument, wyświetlany jest komunikat „Błąd:518”, a jeśli zostanie pominięty pierwszy argument, Calc zaproponuje modyfikację formuły poprzez pominięcie pierwszego średnika i w tej sytuacji drugi argument staje się pierwszym, trzeci drugim, a trzeci jest pominięty. Jeżeli pominięto i drugi argument, kolejny komunikat zaproponuje usunięcie także tego średnika. Gdy zaproponowana modyfikacja zostanie odrzucona, formuła wyświetli „Błąd:511”, jeśli przyjęta – formuła przyjmie postać =JEŻELI(arg) i wyświetli wartość PRAWDA, gdy argument ma wartość różną od zera albo FAŁSZ, gdy ten argument ma wartość zerową. Jeśli pierwszy argument nie będzie liczbą, w obu wersjach programu Calc wynikiem jest błąd #ARG!.

W przypadku tego schematu brakują akcje związane z wartością logiczną FAŁSZ. Jest to ostatni argument funkcji JEŻELI więc jego pominięcie oznacza przyjęcie wartości 0. Schemat unaocznia także fakt, że jakiekolwiek działania dotyczą tylko takiego przypadku gdy wartość D2 wynosi 6. Badanie w ścieżce odpowiadającej za spełniony warunek D2=6 warunku D2=7 lub D2=1 jest bez sensu, bo D2 w tej ścieżce to przecież 6.

Zwróćmy także uwagę na fragment schematu zawierający wyrażenia logiczne E2<=6 oraz E2>6. Już pierwsza relacja oznacza, że pójście ścieżką FAŁSZ to ścieżka, w której E2>6 więc to badanie nie jest potrzebne. Podobnie jest z dwoma ostatnimi warunkami decyzyjnymi. Jeśli E2 nie spełnia warunku, że E2<=9,5 to wiadomo, że jest większe od tej liczby. Można przypuszczać, że formuła powinna odpowiadać takiemu schematowi:

W tym schemacie nie jest rozwiązany do końca warunek D2=1. Pominięto ostatni argument funkcji JEŻELI i zgodnie z tym, co już napisałem, dla wszystkich pozostałych wartości D2 zostanie przypisana wartość 0.

Tworząc formuły oparte o funkcję JEŻELI warto przypomnieć sobie wyrażenia logiczne. Poniżej kolejna formuła z tego samego forum:

=JEŻELI(D2=6;JEŻELI(E2>6;SUMA(E2-F2);0))

Odpowiada ona takiemu schematowi:

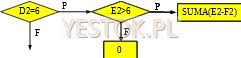
W tej formule oczywiste jest, że zastosowanie funkcji SUMA do wyrażenia E2-F2 jest bezsensowne, gdyż już wyrażenie E2-F2 zwraca wartość będącą oczekiwanym wynikiem.

W powyższej formule komórka przyjmuje, jak widać albo wartość odejmowania E2-F2 (i dzieje się to tylko wtedy gdy D2=6 i jednocześnie E2>6) albo zero w pozostałych przypadkach. W tym wyrażeniu także pominięty został ostatni argument pierwszej funkcji JEŻELI więc wartość 0 jest przypisywana dla każdego warunku, gdy D2<>6.

Skorygowany schemat może więc wyglądać następująco:

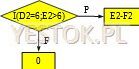
Pierwszym wyrażeniem funkcji możne zatem być wyrażenie logiczne wykorzystujące funkcję I, które będzie generowało wynik PRAWDA tylko wtedy gdy oba warunki będą spełnione.

=JEŻELI(I(D2=6;E2>6);E2-F2;0)

Tylko czy na pewno trzeba w tej sytuacji zastosować funkcję JEŻELI? Pamiętajmy, że wartości logicznej PRAWDA otrzymywanej jako wynik wyrażenia logicznego odpowiada arytmetyczna wartość 1 natomiast wartości FAŁSZ – arytmetyczna wartość 0. Tę formulę można więc zastąpić następująco:

=(E2-F2)*I(D2=6;E2>6)

albo wręcz tak:

=(E2-F2)*(D2=2)*(E2>6)

W pierwsze postaci tej formuły funkcja I zwróci wartość 1 albo 0. Wiadomo, że każda wartość liczbowa pomnożona przez 1 daje tę samą liczbę a przez 0 – zero. W drugiej postaci obliczenie różnicy E2-F2 nastąpi tylko wtedy gdy oba wyrażenie logiczne będą prawdziwe, czyli arytmetycznie wyniosą 1.

Kończąc temat schematów blokowych, poruszę jeszcze jeden jego aspekt, wynikający z wcześniejszego stwierdzenia, że każdy argument funkcji może być dowolnym złożonym wyrażeniem. Gdy takim wyrażeniem ma być pierwszy argument funkcji JEŻELI jego schemat formalnie należałoby umieścić wewnątrz bloku decyzyjnego, albowiem w nim wpisany jest pierwszy argument. Taki sposób prezentacji schematu jest trudny do analizowania ponadto niełatwy do wykonania graficznego. Dlatego warto takie złożone wyrażenie rozrysować jako oddzielny schemat blokowy, nadając temu schematowi jakąś nazwę i nazwę tę wpisać do podstawowego schematu wewnątrz bloku decyzyjnego w postaci np. „Procedura nazwa”.