Yestok.pl

Opracowanie powstało w oparciu o wersje programów do jakich miałem dostęp w trakcie jego pisania: Libre Office: 4.2.6, Apache OpenOffice: 4.1.1, Google Docs – tzw. nowa wersja Arkuszy Google, Excel 2007

Tworzenie prostych formuł obliczeniowych nie stwarza zazwyczaj problemów. Chociaż dla osób, które sporadycznie stykają się z programem typu arkusz kalkulacyjny, a na dodatek mają coś w rodzaju awersji do matematyki, mogą i one przysparzać wątpliwości co do poprawności konstrukcji. Spotkałem się np. w jednym z projektów z formułą zapisaną w taki oto sposób: =SUMA(B11+B12+B13). Z punktu widzenia formalnego jest to całkowicie poprawna formuła, podająca prawidłowy wynik. Autor tego projektu sądził, że tak właśnie należy zapisać sumowanie i zgłosił się z pytaniem, jak obliczać różnicę. Ten przykład świadczy o tym, że intuicyjne korzystanie z oprogramowania nie zawsze jest najlepszym rozwiązaniem. Warto, zanim zacznie się tworzyć projekt oparty o programy arkuszowe, poznać zasady funkcjonowania tych programów. Tym, którzy zastanawiają się dlaczego przytoczyłem ten przykład wyjaśnię, że funkcji SUMA używa się do obliczenia sumy liczb podanych jako argumenty tej funkcji. Można podać do 30 argumentów tej funkcji, zatem jej zapis mógłby wyglądać tak: =SUMA(B11;B12;B13). W tej postaci zostały podane trzy argumenty, z których każdy wskazuje komórkę arkusza. W funkcji SUMA każdy argument może określać zakres komórek zamiast pojedynczej komórki, więc formułę można zapisać tak: =SUMA(B11:B13). W tej postaci w funkcji SUMA wykorzystano tylko jeden argument wskazujący zakres komórek podlegających sumowaniu. Ten ostatni sposób zapisu argumentów jest szczególnie przydatny, gdy zsumowane mają być wartości komórek znajdujących się np. od 120. do 350. wiersza w arkuszu. Wracając do początkowego przykładu, taki sam wynik sumowania tych trzech komórek uzyskamy wpisując prostą formułę: =B11+B12+B13. Przytoczony na początku zapis formuły najpierw wyliczy sumę tych trzech komórek, bo argument funkcji podany jako wyrażenie musi zostać najpierw obliczony. Wyliczona suma zostanie podstawiona jako argument funkcji SUMA co oczywiście w efekcie da tę liczbę jako wynik.

O funkcjach programów arkuszowych napisałem w trzeciej części cyklu opracowań „Arkusz kalkulacyjny dla absolutnie zielonych”, do której można przejść wybierając łącze przejdź opracowania.

Czasami konstruując złożony arkusz kalkulacyjny jesteśmy zmuszeni stworzyć rozbudowaną formułę obliczeniową. Taki złożony algorytm wynikać może z obliczeń realizujących skomplikowany wzór, ale często wynika z próby wykonania obliczeń warunkowych, w których wielokrotnie zagnieżdżone funkcje JEŻELI komplikują całą formułę. Takie formuły są trudne do przeanalizowania, szczególnie wtedy, gdy coś w nich trzeba poprawić a robimy to w kilka tygodni lub miesięcy po zamknięcia projektu.

W tym opracowaniu chciałbym pokazać trzy różne podejścia do tworzenia złożonych formuł obliczeniowych.

Przeanalizowanie formuły.

Czasami warto poświęcić czas na dokładne przeanalizowanie formuły po to by uprościć jej strukturę. Budując formułę robimy to często spontanicznie i intuicyjnie w sposób, w jaki postrzegamy problem w tym momencie swojej pracy. Jednak przeanalizowanie formuły może doprowadzić do jej uproszczenia.
Na jednym z forum znalazłem np. formułę zbudowaną tak:

Nazwy STA, SZER, WYS, MQ i MQMY są w tej formule nazwami przypisanymi do konkretnych komórek i zastępują adresy tych komórek. O nazywaniu komórek i obszarów napisałem – i umieściłem w serwisie – oddzielne opracowanie. Jest ono zadedykowane programowi Calc ale zasady korzystania z nadanych nazw są we wszystkich programach arkuszowych takie same.

Zapiszę teraz osobno wyrażenia obliczane w zależności od spełnienia, bądź niespełniania warunku:

Po pierwsze, łatwo zauważyć, że nawiasy zastosowano w tych wyrażeniach niepotrzebnie. Zgodnie bowiem z zasadami wykonywania obliczeń, mnożenie i dzielenie ma pierwszeństwo przed dodawaniem i odejmowaniem i nawiasy nie wnoszą niczego do kolejności obliczeń. Wyrażenia te można zatem zapisać tak:

Po drugie, zauważmy, że tak naprawdę od warunku znajdującego się w funkcji JEŻELI zależy tylko czwarty sumowany składnik, a dokładnie, od tego warunku zależy czy do przemnożenia wybrana zostanie wartość MQ, czy MQMY. A to oznacza, że całe wyrażenie można byłoby zapisać tak:

To jeszcze nie koniec tej analizy. W tej formule w kilku miejscach dokonywane jest dzielenie przez 1000. Tak naprawdę to dzielenie przez 1000000 jest dzieleniem przez 1000 i jeszcze raz przez 1000. By zmniejszyć liczbę działań można formułę zapisać tak:

Omówię jeszcze wnętrze funkcji I. W pierwszym argumencie tej funkcji mnożymy dwie liczby po to, by je natychmiast podzielić przez 1000000 i porównać z wartością 5,8. Można usunąć to dzielenie, gdyż nie jest ono tu niezbędne. Formuła przyjmie więc postać:

Analizując jednak dokładniej funkcję I zauważamy, że badane są w niej następujące warunki, tym razem zapiszę je symbolicznie: x*y≤5800000 i y<2700. To oznacza, że tak naprawdę x≤5800000/2700, czyli x nie może być większe niż 2148. Ostatecznie formułę można zapisać następująco:

Analizując formułę spróbujmy więc spojrzeć na nią jak na wielomian, który należy napisać w najprostszej postaci.

Podział na części.

Jeśli formuła jest wyjątkowo złożona można obliczać wyniki cząstkowe by z nich skorzystać przy obliczaniu ostatecznego wyniku. Te cząstkowe wyniki można umieścić w komórkach arkusza znajdujących się poza obszarem głównego zestawienia.

Jako przykładu chciałbym użyć znajdowanie pierwiastków równania kwadratowego w ogólnej postaci ax²+bx+c=0.

Wiem, że nie wszyscy dobrze się czują z matematyką, więc przypomnę, że takie równanie może mieć: dwa pierwiastki, jeden pierwiastek albo nie mieć rozwiązania w dziedzinie liczb rzeczywistych.

Rozwiązanie równania wymaga obliczenia wartości Δ jako wyrażenia b²-4ac. Jeśli wartość tego wyrażenia jest liczbą ujemną, równanie nie ma rozwiązania w dziedzinie liczb rzeczywistych, gdyż do jego wyznaczenia potrzebna jest wartość √Δ a w dziedzinie tych liczb nie można wyznaczyć pierwiastka z liczby ujemnej.

W pozostałych przypadkach pierwiastki równania obliczane są wg wzoru: co przy wartości Δ=0 oznacza istnienie tylko jednego pierwiastka równania .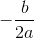

Dla tego przykładu można zapisać dwie formuły warunkowe, które albo obliczą pierwiastki równania, albo poinformują o braku możliwości ich obliczenia.

Układ danych w arkuszu kalkulacyjnym przedstawia ilustracja poniżej.

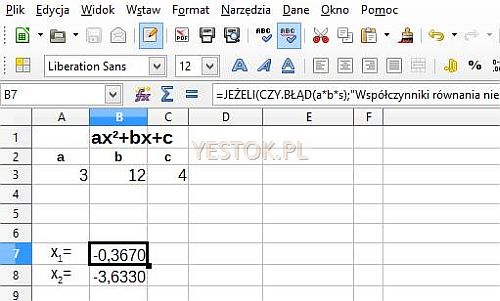
W tym przedstawionym arkuszu nadałem komórkom zawierającym współczynniki równania nazwy „a”, „b” i „s” („s” dlatego, że nie można w arkuszu zdefiniować nazwy „c”) i tych nazw użyłem w formułach zamiast konkretnych adresów.

Gdy obliczenia przygotowujemy na własne potrzeby zazwyczaj nie zwracamy uwagi na, nazwijmy to – poboczne problemy obliczeń. Godzimy się z tym, że może pojawić się wynik w rodzaju #ARG!, #DZIEL/0 czy np. Błąd.502, bo zazwyczaj wiemy, dlaczego się pojawiły. Jeśli jednak opracowany arkusz ma być przekazany do ogólnego użytkowania musimy zbudować go tak aby użytkownik wiedział dlaczego otrzymał takie a nie inne wyniki. Pamiętajmy, że to tylko my tworząc arkusz zakładamy, że jako współczynniki wpisane zostaną liczby. To z tego powodu formuły obliczeniowe stają się takie złożone. Te przedstawione przeze mnie poniżej i tak nie obejmują wszystkich przypadków błędnego wpisania danych wejściowych.

Dla pierwiastka x₁ formuła ma postać:

Formuła obliczana jest na podstawie trzech warunków. Pierwszy sprawdza, czy współczynniki „a”, „b” i „c” są w ogóle liczbami. Można byłoby to sprawdzić przy pomocy funkcji CZY.LICZBA. Trzeba jednak wówczas zbudować wyrażenie logiczne: I(CZY.LICZBA(a);CZY.LICZBA(b);CZY.LICZBA(s)). Funkcja CZY.BŁĄD upraszcza w tym przypadku to badanie. Zwraca ona wartość PRAWDA, gdy argument tej funkcji generuje błąd. Iloczyn współczynników wygeneruje błąd, gdy chociaż jeden z tych współczynników nie będzie liczbą. Druga funkcja JEŻELI sprawdza, czy mamy do czynienia z równaniem kwadratowym (współczynnik a≠0), to sprawdzenie jest ważne, bowiem współczynnik „a” jest dzielnikiem w wyrażeniach obliczających pierwiastki i mogłaby pojawić się sytuacja dzielenia przez 0 (zero). Trzecia funkcja JEŻELI sprawdza, czy istnieje rozwiązanie w dziedzinie liczb rzeczywistych (Δ≥0) i albo wyświetla stosowny komunikat, albo oblicza wartość pierwiastka. Gdy żaden z komunikatów nie został wyświetlony, obliczany jest pierwszy pierwiastek tego równania.

Dla pierwiastka x₂ formuła ma postać:

Ta formuła sprawdza dwa warunki, pierwszy sprawdza, czy w komórce zawierającej wynik pierwszego pierwiastka znajduje się jakiś tekst (tekst znajdzie się tam tylko wtedy, gdy równania nie można rozwiązać). W takiej sytuacji nie wyświetla się żadnego wyniku dla drugiego pierwiastka, bo odpowiedni komunikat wyjaśnia przyczynę. Drugi warunek sprawdza, czy trzeba obliczać drugi pierwiastek równania. Jeśli tak, to jest on obliczany, a jeśli nie, to pojawia się komunikat informujący o tym fakcie.

Ktoś z czytelników może zapytać jak należy interpretować drugą funkcję JEŻELI w aspekcie spełnienia warunku, od którego zależy wykonanie działań (Δ=0). Wpisane w tej funkcji wyrażenie, na pozycji pierwszego argumentu, nie określa bowiem żadnej relacji.

Z zasad funkcjonowania arkuszy wiadomo, że arytmetyczna wartość 0 (zero) jest w odniesieniu do funkcji i wyrażeń logicznych traktowana jako FAŁSZ natomiast każda inna wartość jako PRAWDA. Drugi pierwiastek równania powinien być obliczony, gdy wartość wpisanego wyrażenia jest różna od zera. Wyrażenie obliczeniowe zostało umieszczone na pozycji, w której oczekiwana jest wartość logiczna PRAWDA albo FAŁSZ. Zatem wynik zerowy zostanie potraktowany jako FAŁSZ a każdy inny jako PRAWDA. W drugą stronę działa to nieco inaczej. A więc wynik wyrażenia logicznego wynoszący FAŁSZ, (np. =5<3) arytmetycznie traktowany jest jak 0 (zero) a wynik PRAWDA (np. =I(4>2;7<10)) jak 1. Wykorzystanie tego faktu pokażę w dalszej części opracowania.

Taka konstrukcja formuł jest wskazana wtedy, gdy opracowany arkusz ma być udostępniony do ogólnego wykorzystania. Trzeba się bowiem zabezpieczyć przed sytuacją, w której wpisano niewłaściwe dane i zakomunikować to użytkownikowi.

Ten sam przykład zrealizuję teraz wykorzystując pomocnicze obliczenia. Robię to w tym przypadku tylko po to by pokazać metodologię postępowania. W tym wariancie także chcę zabezpieczyć się przed błędnymi danymi, jednak wykorzystam prostsze formuły. Układ formuł pokazuję na rys. 2.

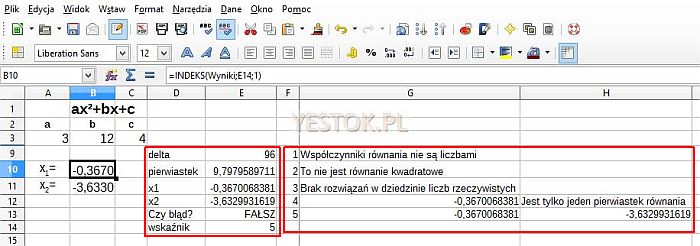
Koncepcja tych obliczeń jest następująca: odpowiednie formuły obliczają wartości delta, pierwiastka z wartości delta i pierwiastki równania, bez względu na to, czy te obliczenia mają sens. Na powyższej ilustracji jest to obszar oznaczony po lewej stronie. Formuły realizujące te obliczenia przedstawiam poniżej.

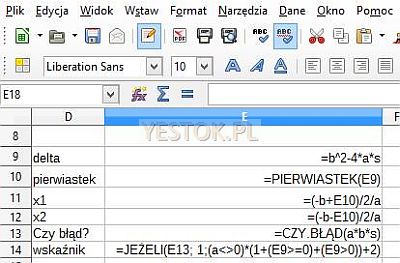
Oprócz tego istnieje dwuwymiarowa tabela możliwych wyników, tabela ta nosi nazwę „Wyniki” i na rysunku 2. jest oznaczona jako obszar po prawej stronie. Tabela zawiera wszystkie możliwe warianty przedstawienia wyników i w arkuszu przedstawia się następująco:

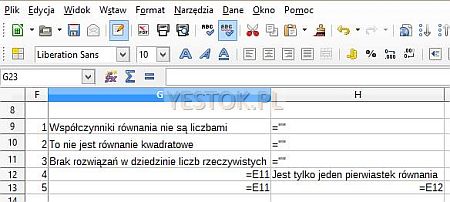
Te komórki tej tabeli, które jako wynik mają przekazać puste miejsce, zawierają wpisany pusty ciąg tekstowy. Wpisywany jest on jako „=""”, czyli znak równości i dwa następujące po sobie znaki apostrofu. Liczby od 1 do 5 znajdujące się po lewej stronie nie należą do tabeli „Wyniki”. Zostały tak umieszczone dla łatwego wizualnego określenia numeru wiersza

Rozwiązanie równania zostanie podane jako określone elementy tej tabeli. Taką możliwość zapewnia funkcja INDEKS. Ma ona trzy argumenty: pierwszy określa tablicę, z której należy pobrać element, drugi definiuje wiersz a trzeci kolumnę w tej tablicy, czyli współrzędne poszukiwanego elementu. Wykorzystanie tej funkcji jest widoczne w pasku wprowadzania formuł na rys. 2. Jako pierwszy pierwiastek zostanie wyświetlona zawartość konkretnego wiersza z pierwszej kolumny tej tabeli a w miejscu drugiego pierwiastka, zawartość z drugiej kolumny tego samego wiersza. Funkcja INDEKS odwołująca się do komórki pustej zwróci jej wartość jako 0 (zero) dlatego komórki puste zostały wypełnione pustym ciągiem tekstowym. Wiersz, z którego te wartości zostaną pobrane określi liczba obliczona na podstawie wprowadzonych danych i obliczeń cząstkowych. Formuła obliczająca ten numer wiersza wygląda tak:

Argument określający warunek w funkcji JEŻELI jest wartością logiczną i wynosi PRAWDA, gdy choćby jeden ze współczynników nie jest liczbą. Gdy więc wartość komórki E13 wynosi PRAWDA, wyliczony numer wiersza wynosi 1, i wyświetlane są wartości z tego wiersza tabeli. Gdy współczynniki są liczbami, czyli wartość komórki E13 wynosi FAŁSZ, obliczany jest numer wiersza jako wynik arytmetyczny działań na wyrażeniach logicznych. Wartość całej formuły wyniesie 2, gdy współczynnik „a” zostanie podany jako zero. Relacja a<>0 z arytmetycznego punktu widzenia przedstawia sobą wartość 0 lub 1. Jeśli „a” będzie wynosiło 0 wartość relacji też wyniesie 0 (FAŁSZ). Mnożenie czegokolwiek przez 0 daje w wyniku także 0, do którego zostanie dodana liczba 2. W drugim wierszu tabeli wyników znajduje się komunikat, iż nie jest to równanie kwadratowe. Pozostałe wyniki zaczynają się od wartości 3 co odpowiada wartościom PRAWDA*(1+FAŁSZ+FAŁSZ)+2), a więc sytuacji, kiedy √Δ<0 a kończą na wartości 5 odpowiadającej istnieniu dwóch pierwiastków równania, czyli PRAWDA*(1+PRAWDA+PRAWDA)+2.

Dzięki takiej konstrukcji formuła generuje numer wiersza dla każdej możliwej sytuacji. Tutaj pokazałem też możliwość wykorzystania wartości logicznej jako liczby. Wspomniałem o tym kilka akapitów wcześniej. Wynikom logicznym PRAWDA odpowiada wartość arytmetyczna 1 a wynikom FAŁSZ wartość 0.

Tak zbudowany arkusz spełnia już swoje zadanie, czyli rozwiązuje równanie kwadratowe. Jednak jako autorzy zazwyczaj nie chcemy pokazywać użytkownikom obliczeń cząstkowych. Wolimy by po wprowadzeniu współczynników zobaczyli oni tylko ostateczne wyniki. Aby to osiągnąć powinniśmy ukryć komórki zawierające formuły pomocnicze.

Arkusze kalkulacyjne pozwalają na ukrywanie wybranych wierszy oraz kolumn, a także na ukrycie całych arkuszy. We wszystkich przytaczanych przeze mnie arkuszach, po zaznaczeniu wybranych kolumn albo wierszy można kliknąć prawym przyciskiem myszy na wyróżnionym fragmencie ramki opisującej wiersze lub kolumny arkusza. Otwarte wówczas zostanie menu kontekstowe a wśród jego pozycji znajdzie się opcja „Ukryj” wiersze lub kolumny. Wybór tej opcji ukryje zaznaczone elementy. Nie będą one widoczne, lecz użytkownik będzie wiedział o tym, że są ukryte, ponieważ na ramce arkusza nie będzie ciągłej sekwencji opisu. Na przykład widać będzie opisy kolumn „A”, „B”, „F”, „G” i następne co oznacza, że kolumny od „C” do „E” są ukryte. Analogicznie jest z ukrytymi wierszami.

Użytkownik takiego arkusza może oczywiście odkryć zakryte elementy i je zobaczyć.

Aby przywrócić wyświetlanie ukrytych elementów arkusza należy zaznaczyć na ramce elementy przylegające z obu stron do tych ukrytych, a następnie po kliknięciu prawym przyciskiem myszy (tak jak przy ukrywaniu) znaleźć opcję w rodzaju „Pokaż”.

Program Calc w obu wydaniach, czyli LibreOffice i Apache OpenOffice ma także odpowiednią akcję w poleceniu „Format – Wiersz” i „Format – Kolumna”. Excel ma w zakładce „Narzędzia główne” w grupie poleceń „Komórki” rozwijane polecenie „Format”, na którego liście znajduje się opcja „Ukryj i odkryj”. Arkusz kalkulacyjny Google Docs wstawia na ramce obszaru, w miejscu ukrytych elementów specyficzny znacznik, którego kliknięcie odsłania ukryte elementy.

Powyżej przedstawiam wygląd tego znacznika po naprowadzeniu nań wskaźnika myszki.

Jeśli autor projektu chce bardziej ukryć obliczenia pomocnicze, może zrealizować je w nowym arkuszu i ukryć cały taki arkusz. Akcje pozwalające ukryć arkusz są dostępne tylko wtedy, gdy projekt składa się z co najmniej dwóch arkuszy (bo co najmniej jeden arkusz musi być zawsze widoczny) a dostęp do nich pojawia się po kliknięciu prawym przyciskiem myszy na nazwie arkusza (na zakładce).

Aby arkusz odkryć wystarczy (w Calcu i Excelu) kliknąć prawym przyciskiem myszy na dowolnej zakładce i wybrać odpowiednio – „Pokaż...” albo „Odkryj...”. Polecenia te otworzą dodatkowe okienko pozwalające wybrać arkusze z listy ukrytych arkuszy. Przykład takiej listy w programie Excel przedstawia rys. 6.

W arkuszu Google Docs pokazanie ukrytych arkuszy realizuje polecenie „Widok – Ukryte arkusze”, które także pozwala wybrać z listy arkusz do odkrycia.

Zmiana koncepcji obliczeń.

W jednym z projektów, które miałem okazję analizować potrzebny był algorytm tworzący ciąg znaków odnoszący się do prostokątnego elementu. Element ten to płyta meblowa o określonej szerokości i głębokości. Dla szerokości i głębokości podawane są dwie dodatkowe liczby mówiące ile krawędzi danego wymiaru ma zostać oklejonych. Liczby te to 0 (zero), gdy żadna krawędź nie będzie oklejana, 1, gdy oklejana będzie jedna krawędź i 2, gdy oklejane będą dwie krawędzie. W takim elemencie (jeśli nie jest on kwadratowy) jeden z wymiarów jest krótszy. Wspomniany ciąg znaków miał dotyczyć wymiarów szerokość i głębokość, w tej właśnie kolejności i podawać ciąg liter „k” i „d” powtórzonych tyle razy ile krawędzi danego wymiaru miało być oklejone. Przy tym litery „k” dotyczyć miały wymiaru krótszego a liery „d” – dłuższego. Jeżeli żadna krawędź nie miała być oklejona wstawiany był ciąg pusty. Tak więc zapis „kdd” oznaczał, że oklejony ma być jeden bok krótszy i dwa dłuższe a np. ciąg „d” oznaczał, że oklejona ma być jedna krawędź dłuższa.

Formułę tworzącą taki ciąg autor zbudował tak:

W tej formule nazwy SZER i GL przypisane zostały do komórek zawierających szerokość i głębokość elementu. Nazwa KS określa komórkę zawierającą liczbę oklejanych krawędzi szerokości a KG – komórkę zawierającą liczbę oklejanych krawędzi głębokości.

Jak widać jest to dość skomplikowana konstrukcja.

W opracowaniu poświęconym funkcjom w arkuszach kalkulacyjnych napisałem, że nie ma potrzeby aby każdy użytkownik znał wszystkie funkcje. Gdy jednak działamy w pewnym specyficznym obszarze działań warto poznać funkcje dotyczące tych obszarów. Zatem gdy działamy na tekstach warto poznać funkcje tekstowe, gdy w obszarze czysto matematycznym – funkcje matematyczne. Warto też poznać funkcje informacyjne, wyszukiwania i adresu. Ich możliwości mogą nieoczekiwanie być bardzo przydatne przy rozwiązaniu wielu problemów.

Przedstawię dwa możliwe sposoby rozwiązania tego zagadnienia. Pierwszy wykorzystuje funkcję POWT (w Google Docs jest to funkcja REPT) należącą do kategorii funkcji tekstowych. Funkcja ta o strukturze POWT(ciąg;krotność) powtarza podany ciąg tyle razy ile wynosi wartość krotności. Gdy wartość krotności jest zerowa, ciąg nie jest wstawiany. Zatem powyższe zagadnienie można rozwiązać następującą formułą:

Formuła tworzy ciąg zależny od zachodzącej relacji i albo łączy literę „k” powtórzoną KS-razy z literą „d” powtórzoną KG-razy albo zamienia te litery w ciągu.

Drugim sposobem, jaki chciałbym przedstawić, jest wykorzystanie funkcji WYSZUKAJ.PIONOWO (w Google Docs VLOOKUP). Funkcja ta bazuje na czterech argumentach. Pierwszy podaje wartość kluczową, która ma zostać odnaleziona w pewnej tablicy. Pozostałe argumenty dotyczą samej tablicy i dodatkowo ostatni z nich jest opcjonalny, czyli nie musi wystąpić. Wykorzystywana jest wielokolumnowa tablica, w której pierwsza kolumna zawiera wartości kluczowe a kolejna – lub kolejne – inne wartości, powiązane lub dotyczące wartości kluczowych.

Klasycznym i doskonale oddającym ideę takiej tablicy przykładem jest tablica, która w pierwszej kolumnie zawiera nazwiska naszych przyjaciół i znajomych, w drugiej numery telefonów do nich, w trzeciej kod pocztowy w kolejnej nazwę miasta a w dalszych informacje, które są powiązane z osobami i uznaliśmy je za ważne. Funkcja WYSZUKAJ.PIONOWO pozwala odnaleźć konkretne szukane nazwisko (czyli zawartość z pierwszej kolumny tablicy) i podać nam informację dotyczącą znalezionej osoby, zapisaną we wskazanej kolumnie takiej tablicy np. numer telefonu albo kod pocztowy.

Pierwszy argument w tej funkcji reprezentuje – jak już wspomniałem – to, co ma zostać znalezione w pierwszej kolumnie tablicy, drugi – określa położenie analizowanej tablicy, trzeci mówi, z której kolumny tablicy ma zostać zwrócona zawartość. Ostatni argument tej funkcji informuje ją czy wpisy znajdujące się w pierwszej kolumnie są uporządkowane we wzrastającym porządku – i wtedy ten argument można pominąć – czy nie. Argument ten wpływa na sposób przeszukiwania tablicy. Gdy tablica jest uporządkowana a poszukiwanego elementu nie ma w tablicy, funkcja zwróci informacje o najbliższym elemencie mniejszym od tego wyszukiwanego.

Gdy więc w naszym przykładowym wykazie nazwisk znajdują się Abaccy, Babaccy, Gedaccy i Laccy, to poszukiwanie Fadackich zwróci dane o Babackich, bo jest to najbliższa wartość leżąca poniżej. Błąd zwróci funkcja tylko wtedy gdy poszukiwana wartość jest mniejsza od pierwszej wartości umieszczonej w tablicy. Ten błąd to: #N/D w Calcu, #N/D! w Excelu albo #N/A w Google Docs i oznacza, że poszukiwana wartość nie została znaleziona.

Gdy za pomocą czwartego argumentu zasygnalizujemy, że tablica nie jest uporządkowana, poszukiwana wartość musi występować w tablicy i jeśli nie zostanie znaleziona generowany jest wspomniany powyżej błąd. Ten czwarty argument przyjmuje wartości logiczne PRAWDA (gdy sygnalizujemy, że tablica jest uporządkowana) albo FAŁSZ (gdy sygnalizujemy, że tablica nie jest uporządkowana). Proszę zwrócić uwagę na to, że ten parametr nie oznacza, że tablica jest naprawdę uporządkowana. On po prostu zadecyduje, w jaki sposób zostaną wyszukane wartości. Jeśli więc w pierwszej kolumnie znalazłyby się liczby (na liczbach chyba lepiej widać sposób działania) 100, 200, 500, 300, 250 a poszukiwanymi wartościami byłyby liczby odpowiednio 250 i 290, to przy pominięciu czwartego argumentu (albo wpisaniu go jako PRAWDA) dla obu przypadków za znalezioną uznana zostałaby wartość 200. Przeglądając bowiem wartości od najmniejszej do największej, funkcja po wartości 200 znalazłaby wartość 500. Algorytm uznałby więc, że – skoro zasygnalizowano, iż tablica jest uporządkowana – najbliższą wartością leżąca poniżej 250, a w drugim przypadku 290, jest właśnie wartość 200. Jeśli czwarty argument wskazywałby na to, że tablica nie jest uporządkowana, czyli zostałby wpisany jako FAŁSZ, to wartość 250 zostałaby znaleziona a dla wartości 290 wygenerowany byłby błąd, bo takiej liczby nie ma w tablicy.

Podsumowując: pierwszy argument funkcji reprezentuje poszukiwaną wartość, drugi argument definiuje zakres komórek zajmowanych przez tablicę, trzeci – podaje, z której kolumny tablicy ma zostać zwrócona odpowiadająca zawartość (kolumny w tablicy są liczone od 1), czwarty określa czy wartości w pierwszej kolumnie mają być traktowane jako uporządkowane (pominięcie tego argumentu jest traktowane jak ustalenie jego wartości na PRAWDA, ponadto argument ten można wpisywać jako liczbę 0 (zero) co odpowiada wartości FAŁSZ lub dowolnej, różnej od zera, co odpowiada wartości PRAWDA).

Dla rozwiązania omawianego zagadnienia utworzyłem tablicę o trzech wierszach i trzech kolumnach. Przedstawiam to na ilustracji poniżej.

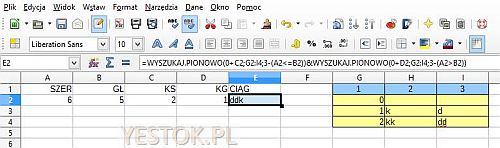
Trzykolumnowa tablica zawiera wartości 0, 1 i 2 w pierwszej kolumnie i odpowiednią liczbę powtórzonych liter. W wierszu odpowiadającym wartości 0 komórki dotyczące liter są puste.

Ciąg tekstowy tworzony jest w komórce E2 jako wynik następującego wyrażenia:

Wyrażenie obliczeniowe składa się z dwóch funkcji WYSZUKAJ.PIONOWO połączonych operatorem łączenia tekstów. Lewa część zwraca ciągi liter zależne od wartości KS a prawa zależne od wartości KG.

Pierwszy argument funkcji to wyszukiwana ilość oklejanych krawędzi. Zapis 0+C2, a w drugim przypadku 0+D2, zapewnia wyszukiwanie wartości 0 wtedy, gdy komórki te pozostaną puste. W przeciwnym razie zwróconą wartością byłby błąd, gdyż wartość komórki pustej jest mniejsza od najmniejszej wartości znajdującej się w tablicy.

Drugi argument, G2:I4 określa położenie tablicy. Trzeci argument jest wyrażeniem obliczającym, z której kolumny ma zostać zwrócony odpowiadający ciąg znakowy. Wyrażenie to wyznacza wartości liczbowe 2 albo 3, zależne od spełnienia bądź niespełnienia relacji. Wyrażenia zbudowane są tak, że jeśli pierwsze z nich wyznaczy wartości 2 lub 3 to drugie wyznaczy odpowiednio wartości 3, lub 2.

Funkcja nie wykorzystuje czwartego argumentu co oznacza, że przyjmie iż wartości w pierwszej kolumnie ułożone są narastająco.

Przedstawione rozwiązanie nie są oczywiście jedynymi możliwymi, można skorzystać choćby z opisanej już wcześniej funkcji INDEKS lub znaleźć jeszcze inne sposoby na rozwiązanie tego zagadnienia. Prezentacja ta miała jedynie pokazać, że do tworzonych formuł można podejść w różny sposób, czasami odbiegający od standardowego spojrzenia na poszukiwane rozwiązanie.