Yestok.pl

Rozpocznę przytoczonym już wcześniej zdaniem, że funkcje są algorytmami obliczeniowymi przygotowanymi przez twórców oprogramowania, ułatwiającymi wykonanie złożonych obliczeń. Funkcjom przypisano nazwy, i zdefiniowano argumenty, pozwalające wskazać wartości, jakie powinny uwzględnić w swoich obliczeniach. Argumenty funkcji zapisywane są zawsze w nawiasach okrągłych postawionych po nazwie funkcji. Argumentami tymi mogą być konkretne liczby, wyrażenia arytmetyczne dające w wyniku liczbę, wyrażenia logiczne, adresy komórek zawierające liczby, wyrażenia tekstowe, zakresy adresów komórek a także inne funkcje. Jeśli funkcja ma więcej niż jeden argument, kolejne oddzielane są znakiem średnika (;). Oczywiście ilość i rodzaj użytych argumentów zależy od konkretnej funkcji. Istnieją też funkcje niewymagające żadnych argumentów, wówczas po ich nazwie występuje tylko pusta para nawiasów „()”.

W arkuszach zdefiniowano bardzo dużo różnych funkcji. W arkuszach Google, jak policzyłem, jest ich 316, w Excelu 340 a w Calcu 409. Funkcje te związane są z zagadnieniami matematycznymi, technicznymi, ekonomicznymi, statystycznymi i wieloma innymi. Użytkownik nie musi się jednak uczyć tych funkcji tylko dlatego, że chce korzystać z programu arkusza. Powinien poznać te, które przydatne są w jego dziedzinie i zagadnieniach jakie rozwiązuje. Funkcje, aby je łatwiej rozpatrywać globalnie, przypisano do pewnych grup tematycznych. W arkuszach Google wyróżniono grupy: daty, inżynieryjne, filtrujące, finansowe, Google, informacyjne, logiczne, wyszukujące, matematyczne, operatorowe, statystyczne, tekstowe, bazodanowe, parsujące i tablicowe. W innych arkuszach grupy są definiowane przez autorów oprogramowania i najczęściej nazywają się podobnie.

Nazwy funkcji utworzono tak, by w lakoniczny sposób oddać ich sens. W arkuszach Google wszystkie funkcje mają nazwy angielskie, lecz w Excelu i Calcu nazwy przetłumaczono na język polski (mówię oczywiście o polskich wersjach programów), tworząc czasami dziwaczną składnię. Wyjaśnię od razu, że stosowane nazwy funkcji nie mają wpływu na wykorzystywanie arkusza w innym kraju. Zatem arkusz z funkcjami zdefiniowanymi w Polsce uruchomiony np. na hiszpańskiej wersji, będzie miał te funkcje nazwane po hiszpańsku. Osobiście byłem i jestem przeciwnikiem „spolszczania” nazw funkcji, czy wspomnianych już nazw wartości logicznych. Bo albo my, Polacy, będziemy mieli kłopoty pracując na obcojęzycznych wersjach arkuszy, albo cudzoziemcy w Polsce będą je mieć, pracując na polskojęzycznej wersji programu.

[Dodane w grudniu 2015 r.] W ostatnio udostępnionej wersji arkuszy Google umożliwiono stosowanie polskich nazw funkcji. Dotychczasowi użytkownicy, którzy o tym nie wiedzą zostaną poinformowani o tym stosownym komunikatem. O tym jakich nazw funkcji używamy decyduje ustawiona lub wyłączona opcja „Zawsze używaj angielskich nazw funkcji”. Opcję tę ustawia się po wybraniu polecenia „Plik – Ustawienia arkusza kalkulacyjnego...”.

Wydaje się jednak, że ta możliwość wprowadza niezamierzone zamieszanie. Użytkownicy, którzy mają ustawiony język polski jako język wyświetlania, w momencie gdy poproszą o informacje o funkcji np. XXX (podczas edycji funkcji w komórce wybiorą odsyłacz „Więcej informacji o funkcji XXX”) otrzymają opis dla polskiej nazwy tej funkcji nawet wtedy gdy chcą używać nazw angielskich. Tak samo dzieje się gdy wybiorą polecenie „Wstaw – Funkcja – Wiecej...” [zob. rys. 4.]. W tym ostatnim przypadku czasami pojawiają się opisy z nazwami angielskimi i nie udało mi się ustalić od czego to zależy.

Wygląda natomiast na to, że przy wyborze angielskich nazw można wprowadzać nazwy polskie. Zostaną one automatycznie przekonwertowane na nazwy angielskie. Działa to także w druga stronę. W systemie pomocy opisującym nazwy funkcji, Google odwołuje się do dokumentu związanego z OpenOffice.org, co sugeruje zgodność nazw funkcji z zastosowanymi w tym pakiecie. Jednak w przypadku funkcji AND (jest o niej mowa w dalszej części opracowania) zastosowano nazwę polską ORAZ a nie I jak programie Calc. [Koniec uzupełnienia]

Wszystkie funkcje są szczegółowo opisane w podręcznikach dotyczących arkusza i w systemie pomocy arkusza. Zawsze zatem można przeczytać o wymaganych parametrach, ich rodzaju i składni funkcji. Nazwy funkcji można wpisywać do formuł małymi albo wielkimi literami. We wszystkich arkuszach zostaną one zamienione na wielkie litery. W Excelu i Calcu litery zostaną zamienione na wielkie, w arkuszach Google pozostaną takie jakie zostały wpisane.

Poniżej na rys. 1 pokazuję opis funkcji ROUND dostępny w systemie pomocy arkusza Google Docs.

Na kolejnej ilustracji widać opis do takiej samej funkcji w programie Calc. Spolszczona, w polskiej wersji programu, nazwa tej funkcji to ZAOKR (Zaokrąglaj).

To opracowanie nie jest kursem arkusza kalkulacyjnego, więc nie będę w nim omawiał każdej funkcji. Ale aby dać pogląd czemu mogą one służyć, kilka z nich omówię.
Po nazwie funkcji dostępnej w arkuszach Google podaję, w nawiasach kwadratowych, nazwę adekwatnej funkcji w Excelu i Calcu.

Funkcje matematyczne.

ROUND(arg1;arg2) [ZAOKR]

Na początek przywołana na ilustracjach funkcja ROUND. Zaliczona została do grupy funkcji matematycznych. Przydatna jest, gdy do dalszych obliczeń chcemy przekazać wynik z zadaną dokładnością. Funkcja wymaga dwóch argumentów. Pierwszy to jakaś wartość. Drugi to liczba mówiąca o tym do ilu miejsc po przecinku obliczana wartość ma być zaokrąglona. Pamiętajmy, że mówiąc „jakaś wartość” czy „liczba miejsc po przecinku” mamy na myśli wartości, które wpiszemy samodzielnie, takie które znajdują się w jakichś komórkach i zostaną wskazane jako adresy tych komórek, albo zostaną wyliczone bezpośrednio w funkcji.

Spójrzmy na poniższą ilustrację.

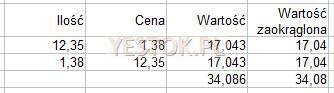
W komórkach kolumny „Wartość” wprowadzono formułę „=B3*C3” oraz „=B4*C4”, co spowodowało wyświetlenie w nich wyników (obu takich samych) 17,043. Zsumowanie tych wyników daje 34,086. Użytkownik mógłby zażądać aby arkusz prezentował te liczby z dwoma miejscami po przecinku. Wówczas liczby 17,043 zostałyby wyświetlone jako 17,04 a wynik sumowania jako 34,09. Arkusz zaokrągla liczby tylko w celu wyświetlenia ich zgodnie z zadeklarowanym schematem, wspominałem o tym pisząc o formatowaniu komórek. Gdybyśmy zatem tak przygotowany arkusz wydrukowali i przekazali odbiorcy, ten szybko udowodniłby nam błędy, gdyż widziałby na swoim wydruku, że 17,04+17,04=34,09.

W komórkach kolumny „Wartość zaokrąglona” wpisałem zatem formułę „=ROUND(B3*C3;2)” oraz „=ROUND(B4*C4;2)”. Pierwszym argumentem funkcji ROUND jest wyrażenie arytmetyczne obliczające iloczyn. Drugi argument mówi, że obliczona wartość ma zostać zaokrąglona do 2 miejsc po przecinku. Argumenty są rozdzielone znakiem średnika. Teraz wyniki są przekazywane do dalszych obliczeń jako 17,04 więc ich suma to oczywiście 34,08. Zaokrąglanie przy pomocy funkcji ROUND liczb do dwóch miejsc po przecinku, wcale nie oznacza, że będą one tak wyświetlane. Wyobraźmy sobie, że funkcja zaokrąglić ma liczbę 2,497. Wynikiem zaokrąglenia będzie w tym przypadku liczba 2,5. Jeśli komórka, w której umieszczono tę funkcję nie ma przypisanego żadnego formatu liczbowego, to wyświetlona zostanie liczba 2,5. Dopiero zastosowanie formatu liczbowego z dwoma miejscami po przecinku spowoduje wyświetlenie 2,50.

Zaokrąglanie wyników kojarzy się najczęściej z jakąś liczbą miejsc po przecinku. Funkcja ROUND idzie dalej. Podanie drugiego argumentu jako liczby ujemnej określa rząd zaokrąglania liczby całkowitej. I tak „=ROUND(1478,46;-1)” da w wyniku wartość 1480 (zaokrąglenie do pełnych dziesiątków) a np. „=ROUND(1478,46;-3), zaokrąglając do pełnych tysięcy da w wyniku 1000. Zasady zaokrąglania dają się lakonicznie opisać tak: wszystko co jest do cyfry 5, zaokrąglamy w dół, pozostałe, a więc 5 i więcej – w górę.

O funkcji ROUND warto pamiętać, gdyż większość obliczeń analizujących np. sprzedaż, opiera się o ilości towaru, ceny i podatek VAT. Jeśli więc cena towaru wynosi np. 7,85 zł/kg a waga wydanego towaru wyniosła 1,428 kg to obliczona jego wartość wynosi 11,2098 zł a 23% podatek VAT od tej kwoty to 2,578254 zł. Niezaokrąglone końcówki mogą w dalszych obliczeniach spowodować niezłe zamieszanie. Rozważmy taki przykład. Sześć kolejnych komórek sformatowaliśmy z opcją wyświetlania jednej cyfry po przecinku. Do pięciu komórek wpisaliśmy liczby 2,24. Zgodnie z formatowaniem, wyświetlają się one jako 2,2. W ostatniej komórce obliczamy formułą sumę tych liczb. Wynik wyświetla się jako 11,2 (bo formuła uwzględnia 2,24), choć widząc wyświetlone wartości oczekiwalibyśmy 11,0.

Mam nadzieję, że ten dość szczegółowy opis funkcji dał czytelnikowi pogląd na ich znaczenie i wykorzystanie.

Zestaw funkcji grupy matematycznej jest dość bogaty, gdyż przeznaczony jest do realizowania różnego rodzaju analiz technicznych, projektowych, naukowych o charakterze czysto obliczeniowym. Stąd są tu funkcje trygonometryczne, logarytmiczne, funkcje pierwiastkowania i wiele innych. Jedną z funkcji jest funkcja PI(). Funkcja ta, tak samo nazywa się we wszystkich arkuszach i nie ma żadnego argumentu, więc wpisywana jest z parą pustych nawiasów. Funkcja zwraca po prostu wartość liczby π. Zatem jeśli konieczne byłoby obliczenie pola koła, którego promień wpisany został np. do komórki „B3” stosowna formuła miałaby postać „=PI()*B3^2”.

Oto kilka innych funkcji matematycznych:

INT(arg1) [ZAOKR.DO.CAŁK]

Funkcja ma jeden argument, liczbę, i zwraca w wyniku część całkowitą wartości, zaokrągloną zawsze w dół. INT(23,999) da w wyniku 23. INT(C4*1,234) najpierw pomnoży zawartość komórki C4 przez liczbę 1,234 i dopiero wtedy wyznaczy część całkowitą.

SQRT(arg1) [PIERWIASTEK]

Funkcja jednoargumentowa, oblicza pierwiastek kwadratowy z podanej wartości. Jeśli wartość argumentu będzie liczbą ujemną zostanie zasygnalizowany błąd.

SIN(arg1), COS(arg1), TAN(arg1)

Funkcjom trygonometrycznym nie przypisano polskich nazw, więc we wszystkich arkuszach nazywają się tak samo SIN, COS, TAN, czyli sinus, cosinus i tangens. Są funkcjami jednoargumentowymi o wartości argumentu podawanej w radianach. COS(PI()/2) obliczy wartość cosinusa 90°, bowiem π radianów to 180°.

MOD(arg1;arg2)

Funkcji MOD także nie przypisano spolszczonej nazwy. Ma dwa argumenty, z których pierwszy to dzielna a drugi to dzielnik. Wynikiem tej funkcji jest reszta z dzielenia dzielnej przez dzielnik i np. MOD(14;6) da w wyniku 2. Nie należy jednak zakładać, że funkcja dotyczy tylko liczb całkowitych. MOD(23,7;2,45) da w wyniku 1,65.

ABS(arg1) [MODUŁ.LICZBY]

Funkcja jednoargumentowa zwraca moduł liczby będącej jej argumentem. ABS(-23,45) da w wyniku 23,45.

Funkcje statystyczne.

Jednymi z najczęściej wykorzystywanych funkcji są te należące do grupy funkcji statystycznych. Charakteryzującą ich cechą jest to, że argumentem funkcji może być zakres komórek, a argumentów może być 30. Funkcje te wykorzystywane są do obliczania pewnych ogólnych parametrów dotyczących dużych zestawień tabelarycznych. Najczęściej używaną funkcją, nie koniecznie kojarzoną ze statystyką, jest funkcja pozwalająca sumować wszystkie wartości liczbowe znajdujące się w pewnym obszarze arkusza.

SUM(arg1;arg2;…;arg30) [SUMA]

Funkcja może mieć do 30-tu argumentów, z których każdy może być liczbą bezpośrednio wpisaną, adresem komórki, wyrażeniem dającym w wyniku liczbę lub zakresem komórek. Funkcja ta często jest mylnie interpretowana i wcale nie tak rzadko spotykałem się z zapisem w rodzaju: „=SUM(B3+B4+B5)”. Od razu wyjaśnię, że przedstawiony zapis jest formalnie poprawny. W funkcji, w tym przytoczonym przykładzie, występuje jeden argument, będący zarazem wyrażeniem arytmetycznym. Zgodnie z zasadami, najpierw zostanie wyliczone to wyrażenie i jego liczbowa wartość podstawiona jako ten jedyny argument. Funkcja SUM wyliczy zatem sumę jednej liczby, bo zgodnie z zasadami, najpierw zostaną dodane do siebie wartości tych trzech komórek i dopiero tak wyliczona liczba stanie się argumentem funkcji SUM. Czyli wynik będzie taki sam jak wtedy, gdybyśmy w tej komórce napisali wyrażenie „=B3+B4+B5”. Już logiczniej byłoby napisać tę funkcję tak „=SUM(B3;B4;B5)”. Tutaj wymieniono trzy argumenty, oddzielone średnikami, więc funkcja policzy sumę wynikającą z wartości znajdujących się w komórkach B3, B4 i B5. Ten sposób zapisu pozwoliłby na wpisanie jeszcze kolejnych 27. argumentów i pozwoliłby na zsumowanie 30 liczb. Zestawienia są jednak często dużo większe.

Łatwo zauważyć, że w przykładzie sumowane są wartości trzech kolejnych komórek w kolumnie B. Można zatem argument funkcji wpisać następująco „=SUM(B3:B5)”. W tym zapisie znowu występuje tylko jeden argument, mówiący jednak, że chodzi o komórki leżące we wskazanym obszarze, od B3 do B5. Reasumując to co powiedziano o argumentach funkcji, całkiem poprawny byłby zapis taki „=SUM(B3:B5;76;F2;G3:K4;SQRT(SUM(B3:B5))”, w którym występuje pięć argumentów. Pierwszy jest znanym już zakresem komórek leżących w jednej kolumnie, drugi jest po prostu liczbą 76, trzeci – adresem komórki F2, czwarty jest zakresem komórek leżących w wierszu trzecim i czwartym w kolumnach od G do K, w końcu piąty jest wartością pierwiastka kwadratowego z sumy liczb w zakresie B3:B5. Wynik zostałby obliczony poprawnie pod warunkiem, że suma wartości w komórkach B3:B5 nie jest ujemna. Ostatni argument tego zapisu zawiera bowiem funkcję SQRT, a ta zwraca wynik tylko dla liczb nieujemnych, generując informację o błędzie w pozostałych przypadkach.

Stosowanie w funkcjach statystycznych argumentów będących zakresami komórek powala analizować bardzo duże tablice. Trzeba też wiedzieć, że funkcje te pomijają w obliczeniach komórki puste albo nie zawierające liczby. Dla sumowania nie ma to znaczenia, ale dla następnej funkcji, już tak.

AVERAGE(arg1;arg2;…;arg30) [ŚREDNIA]

Ta funkcja statystyczna oblicza średnią z liczb wynikających z jej argumentów. Ci, którzy mając zestawienia choćby 50-cio wierszowe musieli policzyć dla nich średnią na zwykłym kalkulatorze, docenią tę funkcję. Tu można wyjaśnić znaczenie pomijanych komórek. Jeśli w czterech komórkach, dla których użyto funkcji AVERAGE znajdowałyby się np. liczba 4, kolejna komórka byłaby pusta, w następnej liczba 2 a w ostatniej umieszczony byłby wpis „luty”, obliczoną średnią byłaby wartość 3. Komórka pusta i zawierająca napis zostaną pominięte, zatem średnia to (4+2)/2 bo tylko dwie komórki „weszły” do średniej.

AVERAGEA(arg1;arg2;…;arg30) [ŚREDNIA.A]

To funkcja podobna do poprzedniej, ale pomijająca wyłącznie komórki puste. Komórki zawierające tekst są traktowane jak wartość 0 (zero). Wartości logiczne są traktowane odpowiednio jako 0 (zero) dla FALSE i 1 dla TRUE. Dla przykładowych danych przytoczonych powyżej obliczoną wartością byłoby więc 2, (4+2+0)/3. Do obliczania średniej zakwalifikowała się też komórka z wpisem „luty”, a więc trzy komórki.

COUNT(arg1;arg2;…;arg30) [ILE.LICZB]

Funkcja podaje ile komórek, w wynikającym z argumentów obszarze, zawiera liczby. Jeśli funkcję tę zastosowalibyśmy znowu do powyższego przykładu jej wartość wyniosłaby 2, bo w tym obszarze wystąpiły tylko dwie liczby.

COUNTA(arg1;arg2;…;arg30) [ILE.NIEPUSTYCH]

To funkcja zliczająca wszystkie niepuste komórki. Ta funkcja uwzględnia w wyniku występowanie komórek zawierających tekst, liczby i wartości logiczne (FALSE, TRUE).

MAX(arg1;arg2;…;arg30), MIN(arg1;arg2;…;arg30)

To dwie funkcje, które także we wszystkich arkuszach kalkulacyjnych nazywają się tak samo. Pierwsza z nich zwraca jako wynik największą liczbę jaka znajduje się w obszarze podanym jako jej argument. Druga zwraca liczbę najmniejszą. Obie funkcje uwzględniają tylko komórki zawierające liczby.

Funkcji statystycznych jest dużo. W zastosowaniach biurowych, te wymienione wydają się być najczęściej używanymi. Osoby zajmujące się statystyką w szerszym zakresie znajdą tu wiele interesujących ich funkcji.

O tym, że funkcje statystyczne są przez autorów arkuszy traktowane jako ważne, niech świadczy to, że wiele z nich można budować wywołując przycisk na pasku narzędziowym.

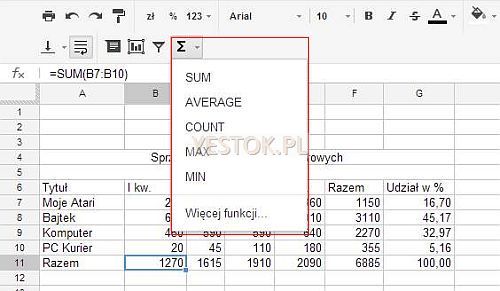
Na powyższym rysunku ikonka oznaczona znakiem symbolu sumowania ∑ może zostać rozwinięta i pozwala wybrać jedną z pięciu funkcji statystycznych. Wybranie funkcji spowoduje wprowadzenie do komórki znaku „=”, nazwy wybranej funkcji oraz pary nawiasów, przygotowanych do wpisania argumentów. Opcja „Więcej funkcji…” widoczna jako ostatnia na liście, powoduje przejście do listy wszystkich możliwych funkcji, poznania ich nazw i wymaganych parametrów.

Funkcje daty i czasu.

Wiele zestawień tabelarycznych zawiera daty i czas jako istotne dane zestawienia. Pojawia się wówczas potrzeba wykorzystania takich danych w rozmaity sposób, dla którego proste przypisanie formatu daty i czasu do komórki może być niewystarczające.

NOW() [TERAZ]

Funkcja nie ma argumentu, więc zapisywana jest w postaci „=NOW()”. Zwraca natomiast liczbę, w której część całkowita odpowiada bieżącej dacie a część ułamkowa czasowi, zgodnie z podanym wcześniej opisem liczb daty i czasu. Data i czas pobierana jest z „komputera” w momencie każdorazowego przeliczania tabeli. Wykorzystanie tej funkcji jako jedynego składnika formuły spowoduje zmianę formatowania komórki, tak aby prezentowała datę i czas w zrozumiały sposób. Zbudowanie formuły zawierającej tę funkcję, np. formuły „=55,5+NOW()” zwróci liczbę daty odpowiadającą 55. dniom i 12. godzinom po bieżącym momencie aktualnej daty. Arkusz Google i Excel zmienią format wyświetlanej liczby na odpowiadający dacie i godzinie, natomiast Calc wyświetli ją jako liczbę daty. Każde przeliczenie arkusza ponownie wyznacza nową wartość funkcji NOW.

TODAY() [DZIŚ]

Funkcja także nie ma argumentu i w odróżnieniu od NOW zwraca tylko liczbę bieżącej daty, pobranej z komputera. Funkcja wyznacza nową wartość daty przy każdym przeliczeniu arkusza.

Sześć funkcji jednoargumentowych potrafi zwrócić konkretną wyekstrahowaną wartość z liczby daty i czasu (albo z dowolnej liczby, która jest przez te funkcje traktowana jako liczba daty i czasu), podanej jako ich argument. I tak funkcja YEAR(arg1) [ROK] zwróci numer roku wynikający z liczby będącej jej argumentem, MONTH(arg1) [MIESIĄC] – zwróci numer miesiąca od 1 do 12, DAY(arg1) [DZIEŃ] – zwróci numer dnia od 1 do 31, przy czym górna wartość dnia wynika oczywiście z miesiąca i roku zawartego w liczbie będącej argumentem tej funkcji. HOUR(arg1) [GODZINA] analizuje ułamkową część argumentu i zwraca wartość odpowiadającej jej godziny, MINUTE(arg1) [MINUTA] poda zawarte w ułamku minuty i w końcu SECOND(arg1) [SEKUNDA] – sekundy. Zapis „=YEAR(41200)” zwróci wartość 2012 bo temu rokowi odpowiada ta liczba, natomiast „=MONTH(41200)” zwróci 10, bo liczba ta odpowiada dziesiątemu miesiącowi w roku 2012.

DATE(arg1;arg2;arg3) [DATA]

Ta funkcja ma trzy argumenty, pierwszym jest rok, drugim miesiąc podany jako liczba od 1 do 12 a trzecim dzień jako wartość od 1 do ostatniej możliwej w danym miesiącu i roku. Na podstawie tych argumentów funkcja wylicza liczbę daty. Zapis „=DATE(2013;6;1)” wyliczy liczbę daty dla 1 czerwca 2013 roku.

Funkcje logiczne

W rozdziale poruszającym formuły logiczne podałem jak są zbudowane. Wyrażenia te zwracają jak pamiętamy wartość logiczną TRUE lub FALSE, i tyle. Przypomnę tylko, że w polskojęzycznych wersjach programów Calc i Excel wartości te wynoszą odpowiednio PRAWDA i FAŁSZ. W przeprowadzanych analizach potrzebne są czasami bardziej złożone wyrażenia logiczne, takie które potrafią wykorzystać zestaw kilku różnych takich wyrażeń. Wyobraźmy sobie, że prowadząc wypożyczalnię płyt DVD zbudowaliśmy w arkuszu kalkulacyjnym zestawienie zawierające m.in. wiek osoby wypożyczającej oraz liczbę dni spóźnienia w zwrocie płyty. Przykład takiego zestawienia na poniższej ilustracji.

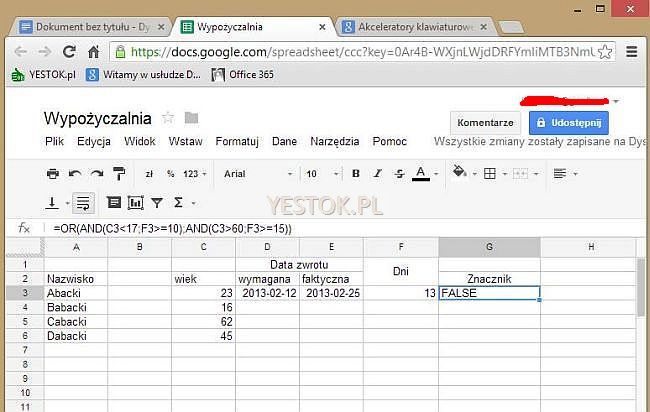
Chcemy teraz oznaczyć wartością TRUE te osoby, które mają mniej niż 17 lat albo więcej niż 60, bo od nich nie pobierzemy opłaty za przedłużenie terminu zwrotu. Zobaczmy to na przykładzie jednej osoby, przyjmując, że jej wiek zapisany jest np. w komórce C3, zaś samo oznaczenie chcemy mieć w komórce G3. Aby oznaczyć osoby młodsze niż 17 letnie w komórce G3 należałoby wpisać „=C3<17” . Ten zapis wyświetliłby wartość TRUE gdyby liczba w C3 była mniejsza od 17. W pozostałych przypadkach wyświetliłaby się wartość FALSE. Zakładamy jednak, że wartość TRUE powinna wyświetlić się także wtedy, gdy wypożyczający ma ponad 60 lat. Formułą logiczną, która to weryfikuje jest „=C3>60”, tyle że komórka G3 jest już zajęta. Tu właśnie przydadzą się funkcje logiczne. Funkcje te mogą mieć do trzydziestu argumentów. Każdy argument musi być wartością logiczną albo zwracać wynik takiej wartości.

OR(arg1;arg2;…;arg30) [LUB]

Funkcja logiczna OR zwraca wartość logiczną TRUE wtedy gdy przynajmniej jeden z jej argumentów ma wartość TRUE. Wykorzystując tę funkcję możemy więc rozwiązać problem wypożyczających, wprowadzając formułę złożoną z funkcji OR. Oto ona „=OR(C3<17;C3>60)”. Tutaj funkcja wykorzystuje dwa argumenty. Wiadomo, że jeśli pierwszy argument jest prawdą, to drugi jest nieprawdą. Jeśli drugi jest prawdą to pierwszy jest nieprawdą. Ale ponieważ jeden z nich jest prawdą, to i wartość funkcji jest także prawdą czyli TRUE. Zdarzenie, że oba argumenty są prawdą, nie może zajść, bo nie można przecież być równocześnie młodszym od siedemnastolatka i starszym od sześćdziesięciolatka. Może wystąpić zdarzenie, że oba argumenty zwracają wartość FALSE, np. ktoś ma 40 lat, ale wtedy funkcja OR zwraca wartość FALSE bo żaden z argumentów nie przyjmie wartości TRUE.

AND(arg1;arg2;…;arg30) [I, ORAZ]

Nazwa tej funkcji w wersjach arkusza Calc jest jednoliterowa i jest to litera „i”. W arkuszu kalkulacyjnym Excel nazwą funkcji jest „ORAZ”. Funkcja zwraca wartość TRUE tylko i wyłącznie wtedy gdy wartości wszystkich argumentów tej funkcji będą miały wartość TRUE. Zmieńmy przykład przedstawiony powyżej na taki, w którym chcemy oznaczyć tylko młodych wypożyczających, którzy przetrzymali płyty ponad 10 i więcej dni (bo od takich pobierzemy opłatę karną). Dla tego przykładu założę, że liczba przeterminowanych dni, znajduje się w komórce F3. Tutaj stosowne wyrażenia logiczne miałyby postać: „C3<17” i „F3>=10” ale musiałyby być spełnione łącznie. Zastosowane wyrażenie logiczne wykorzystałoby funkcję AND następująco: „=AND(C3<17;F3>=10). Formuła zwróci wartość TRUE tylko wtedy gdy osoba będzie miała mniej niż siedemnaście lat a liczba w komórce F3 będzie równa 10 lub większa. Zastosowana w przykładzie funkcja AND wykorzystała dwa argumenty.

Łączenie tych funkcji pozwala budować naprawdę złożone badania. Posiłkując się powyższym przykładem załóżmy, że wartością TRUE oznaczyć chcemy osoby wymienione powyżej ale także co najmniej sześćdziesięciojednolatków, którzy przetrzymali płyty ponad 14 dni. Formuła logiczna wyznaczająca tę oczekiwaną wartość miałaby postać
„=OR(AND(C3<17;F3>=10);AND(C3>60;F3>=15))”.
Tutaj funkcja OR ma także dwa argumenty, tyle że każdy z nich jest funkcją AND o kolejnych dwóch argumentach. Zgodnie z wcześniejszym stwierdzeniem, że najpierw wyznaczane są wartości funkcji najbardziej zagnieżdżonych, wyznaczone zostaną wartości funkcji AND i to one zadecydują o ostatecznej wartości funkcji OR.

Tę sytuację prezentuje rys. 5. Formułę widać w wierszu wprowadzania, gdyż aktywną komórką jest G3. W samej komórce wyświetlona jest wartość FALSE, bo dane w odpowiednich komórkach trzeciego wiersza taką wartość wyznaczyły.

NOT(arg1) [NIE]

Ta funkcja logiczna ma tylko jeden argument, którym musi być wartość logiczna albo wyrażenie logiczne, a jej działanie polega na zaprzeczeniu wartości jej argumentu. Jeśli zatem wyznaczony argument funkcji NOT będzie miał wartość TRUE to funkcja zwróci wartość FALSE. Jeśli wyznaczoną wartością argumentu będzie FALSE, to funkcja zwróci wartość TRUE.

Gdybyśmy więc zmienili zdanie co do oznaczenia wypożyczających i chcieli widzieć wartość FALSE przy osobach, które tak przetrzymały płyty, a TRUE przy pozostałych (bo np. w podziękowaniu za terminowe zwroty dajemy im jedno wypożyczenie za darmo), to formuła logiczna przybrałaby postać: „=NOT(OR(AND(C3<17;F3>=10);AND(C3>60;F3>=15)))”. Ten jeden argument funkcji NOT, jak widać, jest złożonym wyrażeniem logicznym. Oczywiście można formułę realizującą nasz zamysł stworzyć bez użycia funkcji NOT.

IF(arg1;arg2;arg3) [JEŻELI]

To ostatnia funkcja logiczna jaką omówię, ale jednocześnie bardzo często stosowana. Funkcja ta umożliwia bowiem zadeklarowanie dwóch różnych formuł dla jednej komórki, uzależniając która z formuł zostanie wykonana od spełnienia warunku. Funkcja ma trzy argumenty, które schematycznie można przedstawić tak IF(wyrażenie logiczne;wyrażenie1;wyrażenie2). Działanie tej funkcji jest następujące: jeżeli wyrażenie logiczne, które jest pierwszym argumentem funkcji, ma wartość TRUE, to wynikiem funkcji będzie wykonanie wyrażenia1. W przeciwnym razie, czyli gdy formuła logiczna będzie miała wartość FALSE, wykonane zostanie wyrażenie2.

Jak to przedstawić w warunkach naszej wypożyczalni? Załóżmy, że w drugiej kolumnie zestawienia, czyli kolumnie B, wprowadziliśmy pozycję „Kara”, w którym znajduje się kwota kary za opóźnienie zwrotu liczona np. po 75 groszy za każdy dzień opóźnienia. Jeżeli opóźnienia nie ma, w komórce tej kolumny ma się pojawić napis „O.K.”. Załóżmy że karę musi zapłacić każdy, ale młodzież i starsi tylko wtedy gdy przekroczyli terminy podane w poprzednim przykładzie.

Schemat funkcji IF będzie więc następujący, jeśli klient ma zapłacić to należy wyliczyć formułę „F3*0,75”. Cały czas jest to formuła dla komórki w trzecim wierszu naszej tablicy. Jeśli nie ma naliczonej kary, powinien pojawić się napis „O.K.”. Formułę IF do komórki B3 można zatem wpisać tak „=IF(wyrażenie logiczne;F3*0,75;"O.K.")” albo tak „=IF(wyrażenie logiczne;"O.K.";F3*0,75)”. Cała sztuka w ułożeniu wyrażenia logicznego. W pierwszym przypadku musi ono przyjmować wartość TRUE gdy kara ma być naliczona, w drugim wartość TRUE ma zostać wyznaczona wtedy gdy kara nie będzie naliczana. Zastanówmy się zatem jakie warunki muszą być spełnione aby kara była naliczona. Po pierwsze jeśli młodzieniec przetrzymał płytę 10 dni lub dłużej. Zgodnie z tym właściwa będzie funkcja logiczna „AND(C3<17;F3>=10)”, po drugie gdy starszy przetrzymał ją o co najmniej 15 dni, zatem zgodnie z wartością funkcji „AND(C3>60;F3>=15)”, w końcu pozostali, to znaczy tacy, którzy mają od 17 do 60 lat i liczba przetrzymanych dni jest większa od zera, funkcja logiczna dla nich ma trzy argumenty i wygląda tak „AND(C3>=17;C3<=60;F3>0)”. Jeśli dowolne z tych wyrażeń przyjmie wartość TRUE to spełniony będzie warunek do naliczenia kary. Końcową wartość TRUE w sytuacji gdy co najmniej jeden z wielu warunków jest prawdziwy, zapewnia funkcja OR, dlatego ostateczna postać funkcji IF wyglądałaby tak
„=IF(OR(AND(C3<17;F3>=10); AND(C3>60;F3>=15); AND(C3>=17;C3<=60;F3>0));C3*F3;"O.K.")”.
Zobaczmy teraz jak zmieniłoby się wyrażenie logiczne gdybyśmy zechcieli zastosować drugi z wariantów funkcji IF. Pomijam tu zastosowanie poznanej już funkcji NOT, która odwróciłaby wartości logiczne wyrażenia, jeszcze bardziej komplikując i tak dostatecznie złożoną jego postać.

Kto nie płaci? Ten który ma zero dni przeterminowania, czyli prawdą jest wyrażenie „F3=0”, młody który przetrzymał płytę mniej niż 10 dni, zgodnie z wartością funkcji „AND(C3<17;F3<10)” oraz stary gdy przetrzymał płytę o mniej niż 15 dni, co można zapisać funkcją „AND(C3>60;F3<15)”. Ponieważ wystarczy aby dowolny z tych warunków był prawdą, to znowu użyć należy funkcji OR i ostateczna postać formuły w komórce B3 mogłaby wyglądać tak
„=IF(OR(F3=0; AND(C3<17;F3<10); AND(C3>60;F3<15));"O.K.";F3*0,75)”.

W przedstawionych przykładach pojawił się problem budowania złożonego, wielopoziomowego wyrażenia logicznego. Takich złożonych, skomplikowanych formuł, nie tylko logicznych, może być wiele. Rozwiązujemy przecież zagadnienia nie koniecznie sprowadzające się tylko do elementarnych działań. Dlatego osobom zaczynającym przygodę z arkuszami kalkulacyjnymi sugeruję wykorzystywanie innych komórek w arkuszu, traktując je jako pomocnicze, do uzyskania wyników pośrednich i wykorzystanie adresów tych pośrednich obliczeń w formule ostatecznej.

Wrócę do przykładu. W prezentowanej tabeli „Wypożyczalnia” nie korzystamy z kolumn G, H, I oraz dalszych. Możemy zatem wykorzystać komórki tych kolumn do wyliczenia wyników pośrednich. Nieco zmodyfikowaną postać tej tabeli przedstawia rysunek poniżej. Posłużę się tutaj ostatnim wariantem zastosowanej funkcji IF. Aby nie budować skomplikowanego wyrażenia logicznego w funkcji IF, do komórki G3 wpiszę formułę logiczną „=F3=0”. Ta formuła spowoduje, że w komórce tej pojawi się wartość TRUE albo FALSE, w zależności od tego czy komórka F3 zawiera 0 (zero) czy nie. Do komórki H3 wpiszę formułę „=AND(C3<17;F3<10)”. Ta formuła także wyświetli wartość TRUE albo FALSE. W końcu do komórki I3 wpiszę formułę „=AND(C3>60;F3<15)”. W trzech pomocniczych komórkach umieściłem wyrażenia logiczne. Teraz w komórce J3 mogę zapisać nową formułę, dużo prostszą, „=IF(OR(G3;H3;I3);"O.K.";F3*0,75)”. Taki sposób pozwala jednocześnie kontrolować czy nasz algorytm rzeczywiście „liczy” to co żeśmy sobie zaplanowali.

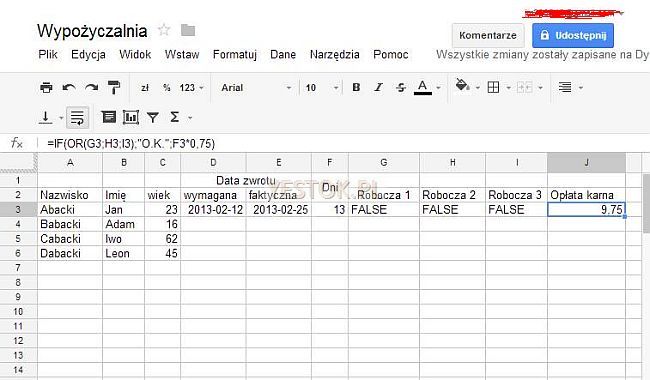
Jeśli sądzisz czytelniku, że w ten sposób tabela staje się nieczytelna, bo zawiera pomocnicze obliczenia, to od razu zapowiem, że poznamy w dalszej części tego materiału jak nie pokazywać tego, czego nie chcemy pokazać.

Zwracam tu uwagę czytelnikowi, że we wszystkich formułach, w miejscach w których chcemy wprowadzić bezpośredni tekst, musi on być ujęty w cudzysłowy. Tak jest z tekstem „O.K.” występującym w formule IF.

Funkcje finansowe.

Z całej grupy funkcji finansowych wybrałem funkcję nazywającą się NPV. Jest to akronim od angielskiej nazwy Net Present Value, a funkcja oblicza bieżącą wartość netto inwestycji. Funkcję tę wybrałem dlatego, że nawet w najstarszych arkuszach kalkulacyjnych, właśnie na „przedpotopowe” ATARI, także taka funkcja występowała. Nie jestem finansistą ale postaram się wyjaśnić jej działanie.

Na początek załóżmy, że dysponujemy kapitałem, powiedzmy 60 000 zł. Zwrócił się do nas inwestor proponujący taki oto układ. My przekażemy mu ten kapitał a on w ciągu pół roku zwróci go nam w sześciu miesięcznych ratach, w następujących kwotach: 10 000, 10 000, 15 000, 10 000, 15 000 i 10 000, czyli zwróci nam de facto 70 000 zł. Czy ta propozycja jest opłacalna? Odpowie nam na to funkcja NPV. Funkcja ma co najmniej dwa argumenty. Pierwszym jest stopa dyskontowa, czyli dla tych którzy nie zajmują się bankami, finansami, inwestycjami itp., po prostu oprocentowanie kapitału w banku. Drugi i ewentualne następne argumenty funkcji to przewidywane wpłaty z inwestycji. Jeśli zatem przewidywane wpłaty umieściliśmy w komórkach od A1 do A6 a oprocentowanie kapitału w banku wynosi np. 7%, to funkcja NPV(0,07;A1:A6) zwróci wartość 55 311,82 zł (po zaokrągleniu). Oznacza to ni mniej ni więcej, że gdybyśmy wstawili tę obliczoną kwotę do banku to też otrzymalibyśmy 70 000 zł. Propozycja inwestora jest zatem dla nas nieopłacalna.

Ponieważ nie jestem bankowcem, finansistą ani nawet ekonomistą, pozostałe funkcje z tej grupy pozostawiam zainteresowanym do samodzielnego przeanalizowania. Wspomniałem tu o niej tylko dlatego iż interesującym wydawał mi się fakt istnienia takiej funkcji w arkuszu kalkulacyjnym z lat osiemdziesiątych ubiegłego wieku, arkuszu który wszystkich funkcji miał 19.

Funkcje wyszukujące.

W tej grupie istnieje wiele interesujących funkcji automatyzujących proces obliczeniowy. Wymienię tu funkcję VLOOKUP(arg1;arg2;arg3;arg4) [WYSZUKAJ.PIONOWO]. Ta funkcja także wchodziła w skład najwcześniejszych arkuszy kalkulacyjnych. Jej przydatność oceni każdy, kto musiał rozwiązać takie oto zagadnienie.

Niech cena jednostkowa towaru przy zakupie zależy od wielkości zakupionej partii. I tak przy zakupie od 1 do 4 sztuk cena wynosi 5 000 zł przy zakupie od 5 do 10 szt. cena jest obniżana o 10%, przy partii 11 do 20 sztuk – o 20%, dla zakresu od 21 do 50 cena obniżana jest o 30% zaś przy zakupie ponad 50 sztuk o 40%. Do zrealizowania tego zadania wykorzystać można właśnie funkcję VLOOKUP.

Aby zilustrować ten problem przedstawiam poniższy fragment arkusza.

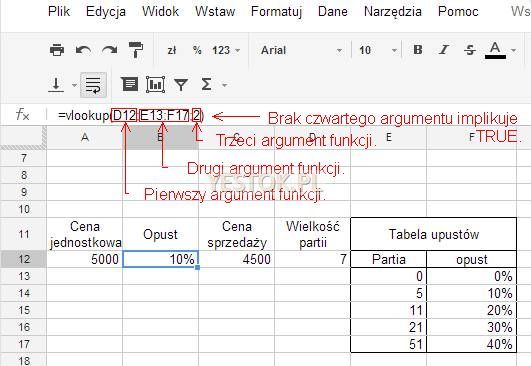
W komórce „Cena jednostkowa” znajduje się podstawowa cena towaru. W komórce „Wielkość partii” jest liczba kupowanych sztuk. W komórce „Opust” ma pojawić się wielkość uzyskanego opustu a w komórce „Cena sprzedaży” wyliczona cena uwzględniająca przyznany opust. Obok znajduje się ułożona tabela opustów. Została umieszczona obok, aby czytelnik widział wszystkie elementy powiązane z tym zagadnieniem, choć tak naprawdę może znajdować się w innym miejscu arkusza, albo na innym arkuszu. W tej tabelce błędnie wpisałem w tytule słowo „upustów” zamiast „opustów”. Komórka aktywna jest komórką, w której ma być wyznaczony opust od ceny sprzedaży wyznaczony przy pomocy funkcji VLOOKUP. Dlatego w wierszu wprowadzania widać wprowadzoną do komórki formułę z przypisanymi argumentami. Funkcja ma cztery argumenty, z których ostatni nie musi występować. Ten ostatni argument to wartość logiczna TRUE albo FALSE i jeśli nie występuje to zakłada się, że podano wartość TRUE.

Zacznę od drugiego argumentu, którym jest pewien obszar komórek zbudowany tak, że pierwsza kolumna tego obszaru zawiera pewne wartości a druga, i ewentualnie następne kolumny, zawierają inne wartości, skojarzone z wartościami pierwszej kolumny. Czwarty argument funkcji mówi o tym, czy wartości w pierwszej kolumnie tego obszaru są ułożone rosnąco, czy nie. W zacytowanym przykładzie, wartości 0 w pierwszej kolumnie, przyporządkowano 0% w kolumnie drugiej, wartości 5 w kolumnie pierwszej przyporządkowano wartość 10% w kolumnie drugiej, i tak dalej. Obszar ten nazwiemy obszarem przeszukiwania. A w omawianym przykładzie podaje on po prostu graniczne ilości sztuk, przy których zaczyna obowiązywać nowa wartość opustu.

Teraz mogę omówić pierwszy argument funkcji, jest nim wartość, która ma zostać znaleziona w pierwszej kolumnie obszaru przeszukiwania. Sposób znajdowania tego argumentu zależy od wartości argumentu czwartego. Jeśli wartością czwartego argumentu jest TRUE (lub gdy jest on pominięty) to wartości w pierwszej kolumnie muszą być posortowane rosnąco gdyż za znalezioną uznaje się wartość, która występuje w pierwszej kolumnie albo najbliższą poprzedzającą poszukiwaną wartość. W przedstawionym przykładzie ma zostać znaleziona wartość 7, ta liczba znajduje się w komórce D12. W przeszukiwanej pierwszej kolumnie nie ma wartości 7 a najbliższą poprzedzającą jest 5 i ona zostanie uznana za znalezioną. Jeśli czwartym argumentem funkcji będzie wartość FALSE, to wartości w pierwszej kolumnie nie muszą być posortowane, ale wtedy funkcja musi znaleźć dokładnie poszukiwaną wartość. Jeśli takiej nie będzie, zgłoszony zostanie błąd.

Trzeci parametr tej funkcji mówi z której kolumny przeszukiwanego obszaru ma zostać zwrócona skojarzona ze znalezioną wartością inna wartość. Kolumny obszaru przeszukiwania liczone są od 1, przy czym 1 jest pierwszą kolumną obszaru. Przyglądając się ilustracji widzimy, że dla znalezionej wartości 5, w drugiej kolumnie skojarzoną wartością jest 10% i ta wartość została wyświetlona w komórce B12.

Przy tworzeniu tej funkcji musimy zdawać sobie sprawę z pewnych ograniczeń. Jeśli funkcja ma działać na posortowanych wartościach pierwszej kolumny (czwarty argument TRUE lub pominięty), to poszukiwanie wartości mniejszej od najmniejszej w tej kolumnie zasygnalizuje błąd. W Google Docs będzie to #N/A (co można tłumaczyć jako not available – niedostępne) w Excelu i Calcu pojawi się #N/D! (niedostępna?). Jeśli pierwsza kolumna nie będzie sortowana (czwarty argument to FALSE), to każda poszukiwana a nie znaleziona wartość, zwróci błąd.
Przy analizie tej funkcji napotkałem na pewne niedopracowanie. Otóż jeśli komórka zawierająca poszukiwaną wartość będzie pusta, to zamiast oczekiwanego wyniku #N/A pojawi się wynik wyglądający jak dwa napisane po sobie znaki minusa (--). Nie jest to jednak wartość tekstowa ani numeryczna, lecz wartość #N/A wyświetlona w taki dziwny sposób.

Jeśli jako wartość trzeciego argumentu zostanie wskazana liczba spoza ilości kolumn w obszarze przeszukiwania, także zostanie zasygnalizowany błąd, błąd o wartości #VALUE. Tutaj dodam, że arkusze Excel i Calc nie są już tak zgodne ze sobą jak w przypadku funkcji i mogą sygnalizować błędy w różny sposób. W tym konkretnym przypadku Excel wyświetli komunikat #ADR!, zaś Calc – Błąd: 502.

Wykorzystując efekty funkcji VLOOKUP można utworzyć teraz formułę dla ceny sprzedaży, która dla powyższego przykładu wygląda tak „=A12*(1-B12)”.

Odpowiednikiem funkcji VLOOKUP dla sytuacji, w której obszar przeszukiwania zorganizowany jest wierszami, jest funkcja HLOOKUP(arg1;arg2;arg3;arg4) [WYSZUKAJ.POZIOMO] o analogicznych argumentach.

Funkcje tekstowe.

Funkcje tekstowe pozwalają na działanie na tekstach. Kilka takich funkcji wymienię, choć ich wykorzystywanie zazwyczaj nie jest domeną początkujących użytkowników.

LEN(arg1) [DŁ]

Funkcja ma jeden argument, którym jest tekst i zwraca długość tego tekstu. Jeśli w komórce, np. B3, wpisano „Pan Jowialski” to funkcja LEN(B3) zwróci wartość liczbową 13, bo z tylu znaków składa się ten tekst.

LEFT(arg1;arg2) [LEWY]

Funkcja ma dwa argumenty, pierwszy wskazuje tekst, drugi podaje liczbę. Wynikiem funkcji jest tekst złożony z tylu początkowych znaków pierwszego argumentu, ile wskazuje drugi argument.

RIGHT(arg1;arg2) [PRAWY]

Jest analogiem funkcji LEFT ale dla końcowych znaków tekstu.

ROMAN(arg1;arg2) [RZYMSKIE]

Funkcja zamienia liczbę na postać rzymską. Funkcja ma dwa argumenty. Pierwszy podaje liczbę arabską do przedstawienia w postaci liczby rzymskiej i musi to być liczba od 1 do 3999. Drugi argument to wartość od 0 do 4. Jeśli nie jest podany, to funkcja traktuje to jak podanie zera. Ten argument decyduje o sposobie prezentowania takiej liczby. Zero oznacza tradycyjny sposób prezentacji, a czym wartość argumentu większa, tym bardziej uproszczona jest taka postać liczby rzymskiej. Funkcja ROMAN(999;0) zwróci CMXCIX, natomiast ROMAN(999;4) zwróci postać IM, co także jest reprezentacją liczby 999.

Zachęcam zainteresowanych do poczytania opisów funkcji w interesujących ich grupach.

W następnej, ostatniej już części opracowania, omawiam problematykę budowania arkuszy. Wyjaśniam znaczenie i rolę adresów względnych i bezwzględnych, kopiowanie i przenoszenie komórek, dodawanie i usuwanie wierszy i kolumn. Poruszam też temat zarządzania arkuszem jako całością. Załączona prezentacja pokazuje od początku do końca proces tworzenia projektu obliczeniowego.

Powrót do części poprzedniej.