Yestok.pl

Opracowanie powstało w oparciu o wersję programu istniejącą w trakcie jego pisania, Libre Office: 4.4.5 i 5.0.1, Apache OpenOffice: 4.1.1.

• Wstęp.
• Wstawianie formuły do dokumentu.
• Tworzenie formuły, równania.
• Symbole stosowane w formułach i wzorach.
• Rozmiar i format formuły i jej elementów.
• Ograniczniki.
• Kontrolowanie formalne formuł.
• Wielkość formuły.
• Tworzenie układów równań.
• Język znaczników.
• Wyrażenia indeksowane.
• Wyrażenia z granicami.
• Funkcje.
• Atrybuty.
• Inne słowa kluczowe.
• Wstawianie równań z ich automatycznym numerowaniem.

Wstęp.

We wszystkich opracowaniach dotyczących nauk ścisłych, technicznych, inżynierskich czy ekonomicznych pojawia się potrzeba zamieszczenia w treści pracy równania albo wzoru a bardzo często wielu równań i wzorów będących nieodłączną częścią opracowania. Zaawansowane edytory tekstów umożliwiają przygotowanie i umieszczenie w tekście obiektu, który może wyglądać np. tak:

Takie rozwiązanie ma także program Writer wchodzący w skład pakietów LibreOffice i Apache OpenOffice. Edytowanie równania w wybranym miejscu dokumentu polega na odwołaniu się do oddzielnego modułu programowego, który pozwala utworzyć lub edytować równanie. Tym modułem jest LibreOffice Math lub OpenOffice Math. Zakończenie edycji umieszcza równanie w dokumencie jako niezależny obiekt. Dalsze zarządzanie takim obiektem odbywa się podobnie jak zarządzanie innymi obiektami np. ramkami czy obiektami graficznymi. Dwukrotne kliknięcie myszką na obiekcie ponownie przywoła moduł redagowania równania i można wprowadzać niezbędne poprawki. Pewną, odbiegająca od obiektów innego typu, właściwością obiektu zawierającego równanie jest to, że nie można zmienić jego rozmiaru.

Nie sposób w tym miejscu nie wspomnieć o całkowicie odmiennym podejściu do edycji dokumentu opartym o środowisko LaTeX. To środowisko programistyczne jest bardzo cenione przez grupy zawodowo zajmujące się edycją. Jego pierwsze wydanie pojawiło się w 1985 roku. Właśnie w tym środowisku pojawił się język znaczników pozwalający konstruować równania matematyczne. Ten język i jego składnia, a przynajmniej logika, zostały w wielu przypadkach przyjęte przez inne systemy tworzenia i edycji równań w tym także we Writerze.

Pod adresem https://latex.codecogs.com/eqneditor/editor.php?lang=pl-pl znajduje się internetowy edytor równań matematycznych online. Obraz utworzonego równanie można zapisać w pliku a następnie umieścić w dokumencie jako obiekt graficzny w potrzebnym miejscu.

Niniejsze opracowanie poświęcone jest jednak edytorowi równań współpracującemu z programem Writer. Dla osób, które z koniecznością wstawiania do opracowania wzorów matematycznych spotkają się sporadycznie, np. przy okazji napisania pracy licencjackiej, edytor może być narzędziem w znacznym stopniu wystarczającym. Niedogodnością edytora jest brak możliwości łatwego i prostego numerowania równań, co w zaawansowanych pracach jest często koniecznością. Wynika to z tego, że w odróżnieniu od innych obiektów, które podpisywane są pod albo nad obiektem, równania podpisywane, czyli numerowane, są z lewej albo prawej strony a takiej możliwości nie udostępnia funkcja podpisu.

Rozwiązanie tego problemu autorzy oprogramowania zaimplementowali w edytorze i takie numerowanie jest możliwe. Choć jest to tylko proteza, to w dokumencie wygląda dobrze. O tym napiszę w dalszej części.

Wstawianie równań i wzorów do dokumentacji podlega także pewnym normom, których należałoby przestrzegać, a przynajmniej o nich wiedzieć. Może trafić się opiekun, promotor lub redaktor opracowania, który będzie zwracał uwagę na każdy szczegół. Warto więc zapoznać się na przykład z opracowaniem profesora Krystyna Pawluka, przewodniczącego Polskiego Komitetu Terminologii Elektrycznej, o tym „Jak pisać teksty techniczne poprawnie”, albo Edwarda Musiała, poświęconego pisowni oraz wymowie nazw jednostek miar. Opracowania te dostępne są na stronach Stowarzyszenia Elektryków Polskich http://www.sep.com.pl [dostęp:15.07.2015] w zakładce Opracowania.

Zanim zajmę się opisem funkcjonowania edytora równań, pokażę pewne przykładowe równanie, w którym wykorzystałem ustawienia właściwości obiektu niewynikające z samej edycji równania. W tym przypadku równanie umieszczone jest na tle struktury gradientowej, ma zdefiniowane dwie krawędzie – górną i dolną – o wybranym kolorze i stylu linii.

Utworzony obiekt zawierający równanie lokowany jest w tekście z atrybutem zakotwiczenia „Jako znak”. Dzięki temu obiekt taki nie jest opływany przez tekst a wyrównanie go na środku realizowane jest przez wyrównanie akapitu a nie przez wyrównanie obiektu.

Pewien dyskomfort może czasami wprowadzać niezbyt estetyczna wizualna postać równania – co widać na ilustracji. Jest to cecha tego edytora. W tym przedstawionym przykładzie symbol sumowania jest umieszczony niesymetrycznie względem środka równania, znak nieskończoności jest mniejszy niż opis dolnej granicy i umieszczony w innej, niż opis dolnego zakresu, odległości od granicy symbolu. Te „niedoskonałości” dają się w pewnym stopniu zmodyfikować, choć nie zawsze w stopniu całkowicie zadowalającym.

[Dodane 17.09.2018] W oddanej do użytkowania wersji 6.0.6 LibreOffice wspomniane powyżej „niedoskonałości” zostały usunięte i przytoczony wzór wygląda obecnie tak jak poniżej.

Jeśli zależy nam więc na bardzo dobrej wizualnej jakości równania, warto skorzystać ze wspomnianej już strony tworzenia równania w systemie LaTeX i wstawić do opracowania obrazy równań.
Niedogodnością takiego postępowania jest konieczność ponownego redagowania równania na stronie internetowej w przypadku potrzeby jego modyfikacji. Dlatego warto nie tylko skopiować do pliku obraz równania, ale także zachować jego prezentację w postaci języka znaczników LaTeX. Pozwoli to wkleić ten ciąg do obszaru redagowania równania w edytorze podczas ponownej edycji.

Przygotowałem równanie przedstawione na pierwszej ilustracji za pomocą wspomnianej strony internetowej. Poniżej można porównać obie metody utworzenia równania.

Wstawianie formuły do dokumentu.

Wstawienie równania wymaga wywołania sekwencji poleceń „Wstaw – Obiekt – Formuła...” co przeniesie użytkownika do nowego otoczenia pracy związanego z działaniem modułu LibreOffice Math albo OpenOffice Math w zależności od używanego pakietu oprogramowania.

Jeżeli zakładamy, że ze wstawianiem równań będziemy mieli częściej do czynienia, można do paska narzędzi dodać ikonę przywołującą edytor (x)Office Math. W obu pakietach procedura jest taka sama. Przedstawię ją na przykładzie Apache OpenOffice:

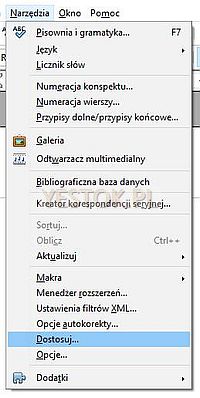
Wywołaj polecenia „Narzędzia – Dostosuj...”

W oknie dialogowym „Dostosuj” wybierz zakładkę „Paski narzędzi”.

Wskaż pasek, w którym ma zostać dodana ikonka. Ilustracja przedstawia dodawanie ikonki do paska standardowego.

Wybierz przycisk „Dodaj...”.

W okienku dialogowym „Dodaj polecenia” znajdź kategorię „Wstaw” a w niej polecenie „Formuła”. Na liście poleceń znajdują się dwa polecenia „Formuła”, wskaż to, któremu przypisana jest ikona zawierająca znak pierwiastka i naciśnij „Dodaj”.

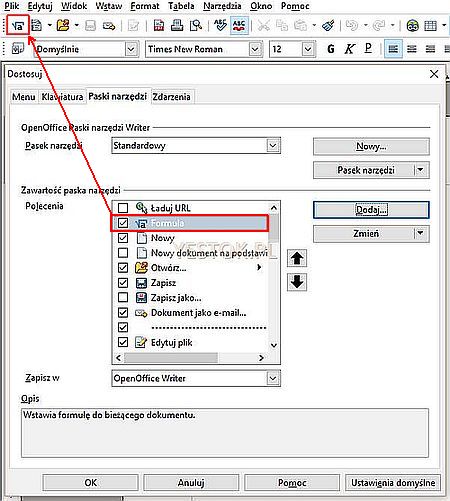
Ikona polecenia „Formuła” została dodana do paska narzędziowego. Teraz przy pomocy przycisków z czarnymi strzałkami znajdujących się w oknie dialogowym „Dostosuj” możesz przenieść tę ikonę do wybranego miejsca na pasku.

Na zakończenie naciśnij „OK”.

Już w trakcie powstawania tego artykułu pojawiła się nowa wersja LibreOffice oznaczona jako 5.0.1, w tej wersji programu standardowy pasek narzędziowy ma już przypisaną ikonkę wywołania edytora formuł. Jest jednak ona oznaczona opcją „nie pokazuj w pasku narzędzi”, dlatego wystarczy w zawartości tego paska ustawić tę opcję na aktywną.

Przywołanie modułu (x)Office Math dla już istniejącego obiektu zawierającego równanie wymaga dwukrotnego kliknięcia tego obiektu.

Wspomniałem już, że zmienia się otoczenie pracy co wiąże się ze zmianą wyglądu okna programu podczas edytowania równań. Okna te różnią się nieco, w zależności od używanego pakietu oprogramowania. W pakiecie Apache OpenOffice będzie ono wyglądało następująco:

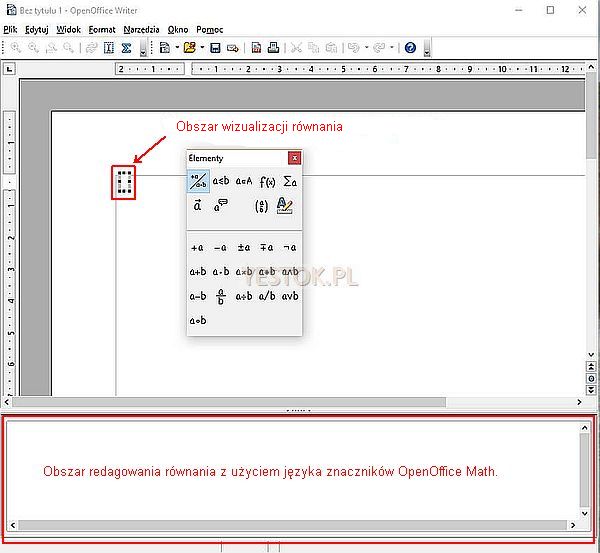
Redagowany dokument zostaje umieszczony w górnej części okna jednocześnie w dokumencie zostanie wyznaczony prostokątny obszar, w którym pojawi się wizualizacja równania. Jeśli edytor został przywołany dwukrotnym kliknięciem istniejącego już równania – pojawi się ono wewnątrz tego obszaru.

W dolnej części tego okna znajduje się obszar redagowania równania nazywany obszarem poleceń. Posługując się znajomością języka znaczników można utworzyć nowe równanie albo zmodyfikować istniejące.

W oknie edytora równań pojawia się pływające okno narzędziowe zatytułowane „Elementy” i zawierające podstawowe struktury, symbole i znaki redakcyjne niezbędne przy tworzeniu równań. To pływające okno narzędziowe można zamknąć. Jeśli nie pojawiło się ono przy zainicjowaniu edytora lub gdy trzeba je ponownie otworzyć należy skorzystać z sekwencji poleceń „Widok – Elementy”.

W oknie „Elementy” w górnej części znajdują się symbolicznie oznaczone kategorie elementów. Pod linią oddzielającą kategorie wyświetlone są, przypisane do zaznaczonej kategorii, szablony, których można użyć podczas tworzenia formuły..

W pakiecie LibreOffice okno edytora równań wygląda następująco:

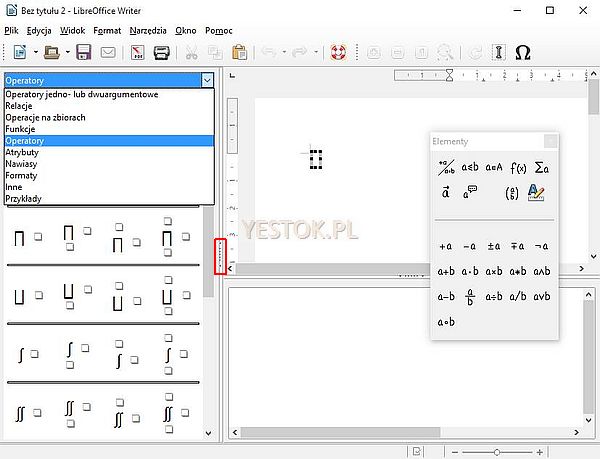
W tym oknie pojawia się dodatkowy lewy panel zawierający szablony, symbole i znaki redakcyjne występujące w pływającym oknie narzędziowym „Elementy”. Panel ten zawiera dodatkową opcję, jakiej nie ma w „Elementach”, nazwaną „Przykłady” i zawierającą kilka wstępnie zdefiniowanych równań. Ponadto w niektórych kategoriach dostępnych jest więcej szablonów. W tej sytuacji okno narzędziowe „Elementy” nie jest uruchamiane, choć oczywiście dostępne. Na potrzeby tej ilustracji wywołałem je sekwencją poleceń „Widok – Elementy” aby czytelnik zobaczył, że jest to takie samo okno jak w wersji Apache OpenOffice. Jeśli ktoś nie chce korzystać z tego bocznego panelu może go ukryć zaznaczonym na rysunku przyciskiem. Ponowne otwarcie panelu możliwe jest tym samym przyciskiem, teraz znajdującym się na lewej krawędzi okna. Boczny panel kategorii można też całkowicie wyłączyć (nie będzie wówczas dostępny) wyłączając opcję „Widok – Dokuj elementy”. We wspomnianej przeze mnie wersji 5.0.1 nie występuje już pływające okno narzędziowe „Elementy” i do dyspozycji jest tylko lewy panel i to on jest włączany lub wyłączany opcją „Elementy” w poleceniu „Widok”, a polecenie „Dokuj elementy” zostało usunięte.

Na powyższej ilustracji przedstawiłem rozwiniętą listę kategorii, ich nazwy, z wyjątkiem kategorii „Przykłady”, pokrywają się z nazwami kategorii znajdujących się w oknie narzędziowym „Elementy”. Widać też, że symbolicznie zaprezentowane szablony zawierają symbole zastępcze (kwadraty) w miejsce oznaczeń literowych wykorzystanych w oknie „Elementy”.

Tworzenie formuły, równania.

Edytory równań mimo drobnych różnic wizualnych działają tak samo. Oba funkcjonują w oparciu o taki sam język znaczników. Utworzenie równania to w istocie zapisanie jego właśnie w takim języku. Sam zapis dokonywany jest w obszarze poleceń a jego odwzorowanie pojawia się w obszarze wizualizacji równania. Osoby często wstawiające do opracowań równania dość szybko opanują składnię tego języka i będą tworzyły równanie z pominięciem wykorzystywania szablonów. Użytkownicy sporadycznie korzystający z opcji wstawiania równania częściej skorzystają z dostępnych „klocków”.

Szablony są symbolicznym przedstawieniem struktury fragmentu tworzonego równania. Wybór konkretnego szablonu wstawia do obszaru poleceń odpowiednią składnię języka a ta jest odwzorowywana w obszarze wizualizacji. Ponieważ podczas wstawiania szablonu nie są znane nazwy zmiennych lub wartości, miejsca, w których powinny one wystąpić zastępowane są symbolami zastępczymi. W obszarze wizualizacji prezentowane są jako puste kwadraty, natomiast w obszarze poleceń – jako znaki zapytania zawarte w ostrych nawiasach „<?>”.

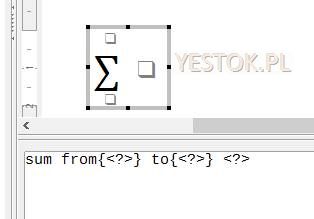
Powyżej na ilustracji przedstawiłem wstawiony szablon z kategorii „Operatory”, symbolizujący operator sumowania w zakresie od—do. Obszar wizualizacji odzwierciedla istotę tego fragmentu równania. W obszarze poleceń pojawił się natomiast zapis składni. Słowa kluczowe tego zapisu to „sum” „from” oraz „to”. „sum” odpowiada za wykorzystany symbol matematycznego sumowania. „from” oraz „to” – jeśli występują – odpowiadają za podanie granic sumowania. Miejsca, w których należy uzupełnić formułę stosownymi wpisami są zastąpione zapisem „<?>”.

Formułę należy zawsze redagować w obszarze poleceń, ponieważ jednak obszar ten jest zsynchronizowany z obszarem wizualizacji wszystkie wprowadzane zmiany znajdują natychmiastowe odzwierciedlenie w tym obszarze.

W OpenOffice Math nie można ustawić kursora w obszarze wizualizacji, jednak kliknięcie myszką wewnątrz tego obszaru automatycznie pozycjonuje położenie kursora tekstowego w obszarze poleceń w miejscu odpowiadającym za kliknięty element równania. Każdy dokonywany wpis ręczny lub wstawiany element dokonuje się w obszarze poleceń i oczywiście ma odzwierciedlenie w obszarze wizualizacji. Aby móc zobaczyć wzajemne odwzorowanie pozycji w obszarze poleceń i prezentowanej postaci równania, należy włączyć opcję „Kursor formuły”. Przedstawia to poniższy rysunek.

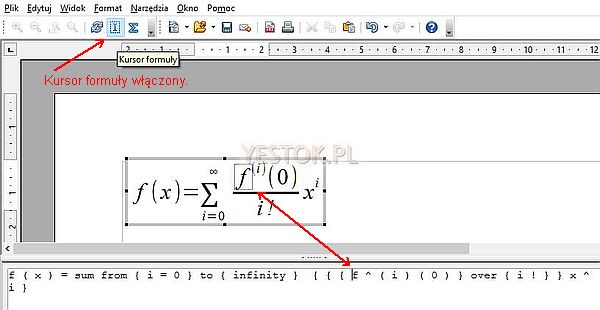
Włączenie kursora formuły, za które odpowiada zaznaczona na ilustracji ikonka spowoduje, że każde miejsce wskazane w wierszu polecenia zostanie odwzorowane w formule, poprzez objęcie tego miejsca przerywaną linią. I odwrotnie, każde wskazane miejsce w formule w obszarze wizualizacji, zostanie otoczone przerywaną linią a w obszarze poleceń kursor tekstowy zostanie umieszczony w stosownej pozycji. Taki sposób funkcjonowania tego mechanizmu pozwala łatwo modyfikować rozbudowane formuły, w których odnalezienie właściwego miejsca w zapisie języka znaczników nie jest takie proste.

Pracując nad tym tematem znalazłem pewne różnice w działaniu tego mechanizmu w LibreOffice Math. Początkowo sądziłem, że dotyczą one pakietu LibreOffice jako całości, jednak dokładniejsze przyjrzenie się tematowi skomplikowało wnioski. Moje spostrzeżenia prowadzą w kierunku stwierdzenia, że nieco inaczej działa ta wersja pakietu w środowisku systemu 32 bitowego a inaczej w środowisku systemu 64 bitowego. Swoje przypuszczenie opieram na tym, że porównałem działanie oprogramowania w systemach: Windows XP Home Edition (jest to system 32 bitowy), w Windows 10 Pro 32 bitowy i Windows 10 Pro 64 bitowy. W 32 bitowych wersjach funkcjonowanie oprogramowania LibreOffice Math jest takie samo jak Apache OpenOffice Math a różnice pojawiają się gdy LibreOffice działa w wersji 64 bitowej. Przypominam, że swoje opracowania tworzę w oparciu o współpracę pakietu z system operacyjnym Windows. W 64 bitowej wersji systemu można ustawić kursor tekstowy wewnątrz obszaru wizualizacji, czego nie można zrobić w wersji 32 bitowej i bezpośrednio w tym obszarze dokonywać wpisów. Natomiast stan przełącznika „Kursor formuły” nie ma żadnego wpływu na funkcjonowanie edytora. Rysunek poniżej pokazuje taka sytuację.

Cienka pionowa linia odpowiada położeniu kursora, zaś podkreślenie wskazuje element, który będzie poprawiany.

Niestety, położenie kursora w obszarze wizualizacji nie ma odwzorowania w obszarze poleceń i odwrotnie. Jednak wprowadzane wpisy mają swoje odwzorowanie w każdym z obszarów. Ale i tutaj pojawia się rozdźwięk w funkcjonowaniu tego mechanizmu. Nie rozwijając tego wątku przyjmuję, że edytowanie formuły bezpośrednio w obszarze wizualizacji nie jest zalecane.

Wspomniałem o synchronizacji zawartości obszaru poleceń i obszaru wizualizacji. Zazwyczaj zmiany zachodzą natychmiast, jednak w rzeczywistości zależy to od ustawionych opcji polecenia „Widok”. Rozwiniętą listę tego polecenia wraz z paskiem narzędziowym „Narzędzia” przedstawia następna ilustracja.

Druga z opcji tego polecenia „Autoaktualizacja widoku” decyduje o tym czy zmiany dokonywane w obszarze poleceń znajdą natychmiastowe odzwierciedlenia w obszarze wizualizacji. Jeżeli autoaktualizacja jest wyłączona to jednorazowe wymuszenie aktualizacji realizuje pierwsze polecenie z tej listy czyli „Aktualizuj”.

Czytelnik zauważy zapewne wyłączone możliwości użycia poleceń znajdujących się w dolnej części rozwiniętej listy. Odpowiedniki tych poleceń są także nieaktywne w widocznym na ilustracji pasku „Narzędzia”. Nie jest to błąd programu. Te możliwości stają się dostępne tylko wtedy, kiedy edytor (x)Office Math zostanie uruchomiony jako samodzielny program, a to jest możliwe po uruchomieniu programu Math albo po wywołaniu sekwencji „Plik – Nowy – Formuła”. Edytor pracujący jako samodzielny program umożliwia utworzenie formuły i zapisanie jej jako odrębnego pliku z nazwą o rozszerzeniu ODF. Dzięki temu można przygotować wstępne szablony rozbudowanych formuł i wykorzystywać je w przyszłych opracowaniach. Aby wstawić do opracowania formułę wcześniej zapisaną jako taki plik, trzeba skorzystać z polecenia „Wstaw – Obiekt – Obiekt OLE...”.

W otwartym oknie dialogowym należy zaznaczyć opcję „Utwórz z pliku” i za pomocą przycisku „Szukaj” („Search”) wskazać właściwy plik do wstawienia.

W tym kontekście trzeba też pamiętać, że plik formuły może zostać zapisany przez edytor tylko wtedy gdy edytor został wywołany jako samodzielny program. Jeśli edytor został przywołany podczas edycji dokumentu, to polecenie „Zapisz” lub „Zapisz jako...” dotyczy całego dokumentu, a nie redagowanej formuły.

Symbole stosowane w formułach i wzorach.

Pasek narzędzi zawiera dwie ważne ikonki: „Kursor formuły”, o którym była już mowa i ikonkę opisaną jako „Katalog”. W wersji LibreOffice Math ikonka prezentowana jest przez grecką literę omega a w wersji OpenOffice Math przez grecką literę sigma. Ikonka „Katalog” otwiera okno dialogowe umożliwiające wstawienie do równania greckich liter prostych albo pochylonych lub symboli specjalnych.

Każdemu symbolowi w tych zestawach przypisana jest indywidualna nazwa. Nazwę tę poprzedzoną znakiem procenta można użyć w obszarze poleceń. Oznacza to wówczas wstawienia tego symbolu do formuły. Tutaj zastosowano pewną prostą metodę mnemotechniczną. Nazwami symboli liter greckich są ich nazwy angielskie, przy czym symbole liter pochylonych zaczynają się literą „i”. Ponadto nazwy określające symbole małych liter są napisane małymi literami a nazwy określające wielkie litery są napisane wielkimi literami. Zatem „%omega” wstawi małą, prostą literę „ω” natomiast „%iOMEGA” wielką, pochyloną literę „Ω”.

Okienko dialogowe umożliwia także dodanie nowych, własnych symboli, które będą mogły być wykorzystywane w formułach. Pokażę to na przykładzie chemicznego zapisu rozpadu chlorku amonu w temperaturze 350 °C (tak zwana dysocjacja termiczna):

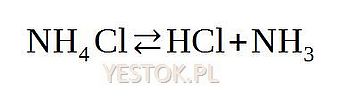
W tym zapisie potrzebny jest symbol podwójnej strzałki. Takiego symbolu nie ma w zestawie symboli dostępnych w edytorze, dlatego dodam go do listy symboli specjalnych.

Po skorzystaniu z ikonki „Katalog” otworzy się okno dialogowe „Symbole” umożliwiające wstawienie wybranego symbolu do formuły ale też umożliwiające edycję symbolu.

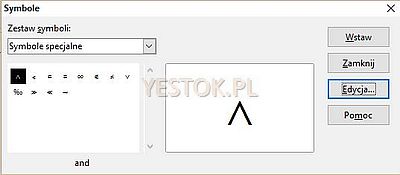
Po przejściu do edycji, otwarte zostanie okno „Edycja symboli”.

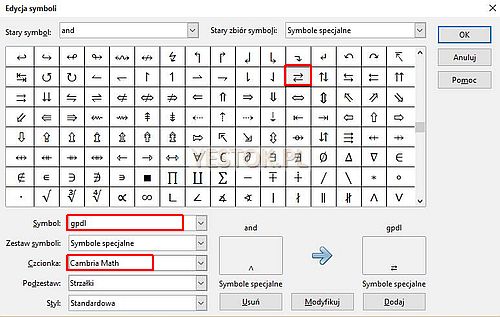
W tym oknie można wskazać nowe potrzebne symbole. Zestaw symboli (x)Office jest tworzony w oparciu o czcionkę OpenSymbol a w tym zestawie znaków nie ma takiej podwójnej strzałki. Jest natomiast w dołączanej do systemu Windows czcionce Cambria Math (nie wiem jak to jest w systemach Linux i Mac ale przedstawiam tylko metodę postępowania). Dlatego najpierw w okienku wyboru czcionki odnalazłem i wskazałem czcionkę Cambria Math. Następnie w symbolach tej czcionki odnalazłem potrzebny element i zaznaczyłem go. W dolnej części, w polu po nazwie „Symbol” pojawi się nazwa zbudowana na podstawie szesnastkowej reprezentacji liczbowej tego kodu. Można tę nazwę nadpisać własną nazwą, w tym przypadku wymyśliłem „gpdl” (górna w prawo, dolna w lewo). Ostatnim krokiem jest użycie przycisku „Dodaj” a następnie „OK”.

Od tego momentu zawartość symboli specjalnych zmieni się.

Dodany symbol znajdzie się na pozycji zgodnej z alfabetyczną kolejnością nazw symboli specjalnych. Jeżeli plik z dodanym symbolem zostanie otwarty na innym komputerze, to symbol ten będzie w nim nie tylko widoczny ale i dostępny. Nie będzie natomiast dostępny w nowych dokumentach otwieranych na tym komputerze.

Rozmiar i format formuły i jej elementów.

Wspomniałem już wcześniej, że nie można zmienić rozmiarów obszaru wizualizacji. Nie można więc tą metodą określić obszaru zajmowanego przez formułę. Można to zrobić tylko za pomocą atrybutów rozmiaru należących do języka znaczników albo za pomocą polecenia „Rozmiar czcionki” znajdującego się na liście poleceń rozwijanego polecenia „Format”.

Kilka słów na temat zawartości polecenia „Format”:

Polecenie „Czcionki...” otwiera okno dialogowe pokazane poniżej.

W oknie można ustalić czcionki dla poszczególnych elementów formuły lub je zmodyfikować. Jednak czynności te nie są wskazane i lepiej jest pozostawić zaproponowane ustawienia.

Polecenie „Rozmiar czcionki...” otwiera poniższe okno dialogowe:

W tym oknie można ustalić podstawowy rozmiar czcionki oraz względne wielkości poszczególnych składowych formuły. To tymi parametrami, a przede wszystkim wielkością czcionki podstawowej, można ustalić graficzną wielkość formuły. Ustalone wielkości odniosą się do całej formuły. Wprowadzone zmiany dotyczą redagowanej formuły, chyba że zostanie naciśnięty przycisk „Domyślnie” co spowoduje ustawienie ustalonych wartości jako domyślnych dla całego pakietu i wszystkich tworzonych od tego momentu formuł.

Polecenie „Odstępy...” pozwala zdefiniować albo skorygować odległości występujące między różnymi elementami występującymi w formule. Wszystkie wartości liczbowe określone są jako wartości względne w stosunku do wielkości czcionki podstawowej.

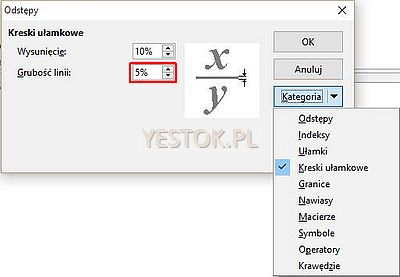
Na pokazanej ilustracji korygowanymi odstępami są te należące do kategorii „Kreski ułamkowe” a po kliknięciu myszką wewnątrz wybranego pola, w okienku podglądu pojawią się symbole ukazujące, jaka wartość będzie zmieniana. Także tutaj można zmienione ustawienia zapisać jako obowiązujące domyślnie.

Polecenie „Wyrównanie...” otwiera okno dialogowe pozwalające określić wyrównanie formuły wewnątrz obszaru wizualizacji. Wyrównanie dotyczy każdego wiersza występującego w formule, także takiego który jest wynikiem wstawionej struktury. W szczególności widać będzie ten wpływ w formułach zawierających ułamki, gdyż liczniki i mianowniki ułamków są traktowane jako wiersze, tyle że wyrównywane w stosunku do zasięgu swojej kreski ułamkowej.

Ostatnie polecenie w tej grupie to „Tryb tekstowy”. Jest to w gruncie rzeczy przełącznik, który zmienia wygląd obszaru wizualizacji w taki sposób aby mógł on stać się częścią wiersza.

Jak już napisałem formułę tworzy się w obszarze poleceń wpisując ją bezpośrednio – co wymaga znajomości składni języka znaczników – albo wstawiając w zaplanowanym porządku szablony z wybranych kategorii. Nie wspomniałem jeszcze o tym, ale obszar poleceń ma jeszcze jedną właściwość, otóż kliknięcie wewnątrz tego obszaru prawym przyciskiem myszy, otwiera podręczne menu z listą kategorii znanych już z polecenia „Elementy” i podwiązaną do każdej kategorii listą zapisów w postaci składni języka znaczników. Wybór składni wstawia ją do formuły w miejscu, w którym znajduje się kursor tekstowy. W odróżnieniu od szablonów, w których układ symboli zastępczych obrazuje jaka struktura zostanie wstawiona, tutaj trzeba znać składnię języka znaczników. Można oczywiście wykorzystywać wszystkie te sposoby równolegle.

Ograniczniki.

Jednymi z wykorzystywanych znaków graficznych wewnątrz formuł są ograniczniki, z których najbardziej znane są nawiasy rozmaitego kształtu. Takie ograniczniki są niezbędne dla określenia kolejności i hierarchii obliczeń, zilustrowania struktury przedstawianego zagadnienia lub zobrazowania innych okoliczności, znanych autorowi prezentującemu formułę. Cechą charakteryzującą ograniczniki jest występowanie ogranicznika otwierającego (lewego) i zamykającego (prawego). Edytor równań kontroluje czy każdy wstawiony ogranicznik otwierający ma odpowiadający mu ogranicznik zamykający i sygnalizuje sytuacje błędne. Jeśli ogranicznikami mają być nawiasy okrągłe albo kwadratowe to można je wpisywać z klawiatury. Nawiasy klamrowe, także często wykorzystywane w formułach, mają w języku znaczników własne znaczenie. Służą do grupowania struktur formuły w celu ich właściwej interpretacji w formule. W prezentowanych wcześniej ilustracjach widać te nawiasy występujące w obszarze poleceń. Tego rodzaju nawiasów nie można więc wprowadzić do wizualnej postaci formuły bezpośrednio z klawiatury.

Aby pokazać znaczenie nawiasów grupujących przedstawię kilka zapisów. Po lewej stronie znajduje się zapis formuły wprowadzony do obszaru poleceń w języku znaczników, po prawej – wizualizacja tego zapisu

Pierwszy przykład nie wymaga komentarza może poza informacją, że osoba nieznająca w ogóle języka znaczników łatwo zorientuje się, że w tym języku słowo kluczowe „over” oznacza ułamek z tradycyjną kreską ułamkową. Taką formułę można utworzyć wykorzystując wstawienie dwóch szablonów. Tak jak to przedstawia poniższa sekwencja rysunków.

W pływającym menu narzędziowym zaznaczyłem te dwa szablony, które zostaną wykorzystane. Liczby widoczne na ilustracji wskazują w jakiej kolejności szablony te zostaną wykorzystane.

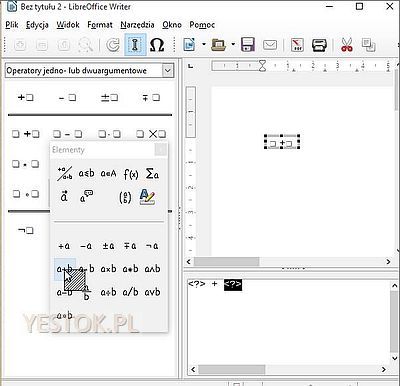
Jako pierwszy został wstawiony szablon „a+b”. W obszarze poleceń widać dwa symbole zastępcze. Po zaznaczeniu drugiego symbolu zastępczego

wstawiłem drugi szablon, szablon ułamka zwykłego, który zastąpił sobą ten symbol zastępczy. Zwróćmy uwagę, że ten szablon wykorzystał nawiasy grupujące, dzięki temu można utworzyć właściwe zawartości licznika i mianownika. Nawiasy te nie byłyby potrzebne, gdyby licznik i mianownik były jednowyrazowymi wyrażeniami, jednak szablon „nie wie” co będzie tymi wyrażeniami.

Drugi przykład pokazuje wykorzystanie nawiasów okrągłych. Zdefiniowały one licznik ułamka we właściwy sposób, ale zostały także umieszczone w liczniku jako składowe części formuły.

Trzeci przykład pokazuje znaczenie nawiasów grupujących. Wyznaczają one formule te składowe, które mają być potraktowane jako jedna grupa, w tym wypadku będąca licznikiem ułamka. Nawiasy te nie pojawiają się jednak w zobrazowaniu formuły.

Przykład czwarty i piąty unaocznia jak zastosowanie grupowania wpływa na wizualną postać formuły.

Ostatni przykład wprowadziłem by przedstawić wygląd zapisu bardziej złożonej formuły i jednocześnie pokazać wykorzystanie słów kluczowych.

Znaki nawiasów klamrowych, jak wspomniałem, należą do tej kategorii słów kluczowych języka znaczników, których nie można w ten sposób wprowadzić do wyglądu formuły, a jednak bardzo często są one w formułach potrzebne. Ponadto w wizualizacji formuł mogą być potrzebne także inne symbole ograniczające. Zestaw przydatnych symboli przedstawia ilustracja poniżej.

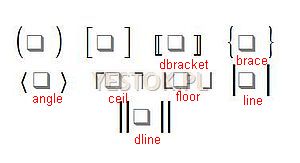
Dla symboli innych niż nawiasy kwadratowe i okrągłe zdefiniowano słowa kluczowe charakterystyczne dla każdej pary nawiasów. Dla łatwiejszego ich zapamiętania każde z tych słów zaczyna się literą „l” (left) jeśli dotyczy symbolu otwierającego i literą „r” (right) – gdy zamykającego.

Zatem trzecią parę symboli widocznych na powyższej ilustracji utworzą: „ldbracket” i „rdbracket” (left double bracket, right double bracket), czwartą: „lbrace” i „rbrace”, piątą: „langle” i „rangle”, szóstą: „lceil” i „rceil”, siódmą: „lfloor” i „rfloor”, ósmą: „lline” i „rline” a ostatnią: „ldline” i „rdline”.

Proszę zwrócić uwagę na to, że ograniczniki „ceil” i „floor” nie występują w postaci szablonów, dostępnych w pływającym zestawie poleceń „Elementy”. Są natomiast dostępne w postaci takich szablonów w bocznym panelu elementów występującym w LibreOffice.

Czasami ze względu na wielopiętrową konstrukcję formuły takie ograniczniki powinny mieć wielkość dopasowaną do wysokości wyrażenia, którego dotyczą. Taką właściwość zapewnia poprzedzenie lewego ogranicznika dodatkowym słowem „left” a prawego dodatkowym słowem „right”. Jeśli zatem chcemy aby wyrażenie było objęte nawiasami okrągłymi o wysokości całego wyrażenia, powinno ono być skonstruowane wg schematu „left ( «wyrażenie» right )”, a gdy nawiasami klamrowymi: „left lbrace «wyrażenie» right rbrace”. Ten rodzaj symboli w terminologii Apache OpenOffice nazywany jest nawiasami skalowalnymi a w LibreOffice nawiasami zmieniającymi rozmiar.

Tylko dla ograniczników dopasowywanych do wysokości wyrażenia można zastosować zapis „left none” albo „right none” oznaczający, że odpowiadający mu w strukturze formuły ogranicznik lewy lub prawy nie ma być ujawniony. Zapis ten zapewnia poprawność formalną dla pary ograniczników i odnosi się do najbliższego ogranicznika, który nie ma swojej pary. Dzięki temu poleceniu bez sygnalizowania błędu można uzyskać efekt taki, jaki widać poniżej.

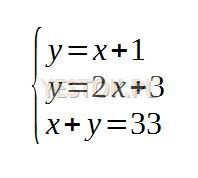
Dla ograniczników zwykłych stosowana jest inne rozwiązanie. Aby edytor nie sygnalizował błędów braku komplementarości należy słowo kluczowe tego ogranicznika poprzedzić znakiem „\” (lewy ukośnik). Dzięki temu można zapisać strukturę taką jak poniżej, przedstawiającą np. zakres prawostronnie otwarty bez zasygnalizowania błędu braku prawego nawiasu kątowego i lewego nawiasu okrągłego.

Kontrolowanie formalne formuł.

Edytor formuł ma wbudowany mechanizm kontroli powstającej formuły. Oczywiście nie sprawdzi on czy prezentowana formuła jest poprawna merytorycznie, sprawdza jednak czy formuła jest zbudowana poprawnie od strony formalnej. A więc, czy zastosowane pary ograniczników lewego i prawego są kompletne, czy nie pominięto jakiegoś wyrażenia w miejscu, w którym powinno ono wystąpić itd.

Poniżej na ilustracji przedstawiam formułę celowo napisaną błędnie. Błąd polega na pominięciu wyrażenia wymaganego po słowie kluczowym „over”.

W obszarze wizualizacji, miejsca, które edytor uznaje za błędne są sygnalizowane znakiem odwróconego czerwonego znaku zapytania. Tego rodzaju błędy mogą zostać usunięte tylko przez skorygowanie formuły do właściwej postaci. Te miejsca łatwo jest odnaleźć w obszarze poleceń, gdyż edytor przenosi kursor tekstowy do kwestionowanego zapisu po naciśnięciu klawisza funkcyjnego F3 (przy przechodzeniu w kierunku końca zapisu) albo kombinacji SHIFT+F3 (przy przechodzeniu w kierunku początku zapisu). Na ilustracji widać znalezione miejsce – w obszarze poleceń – jako zaciemniony prostokąt, ponadto na pasku stanu programu pojawia się komunikat podający wyjaśnienie dotyczące tej zaznaczonej pozycji. W tym wypadku: „Nieoczekiwany znak” oznacza, że przed nawiasem zamykającym grupę powinien znaleźć się jakiś wpis należący do zakresu słowa kluczowego „over”.

Taki błąd nie zostałby zasygnalizowany, gdyby brakujący element zasygnalizowano symbolem zastępczym <?> albo po prostu symbolem pustej grupy, czyli parą nawiasów {}.

Edytor wykorzystuje jeszcze jeden mechanizm dostępu do charakterystycznych miejsc w formule. Klawisz funkcyjny F4 i odpowiednio SHIFT+F4 przenosi kursor tekstowy do najbliższego symbolu zastępczego (odpowiednio w prawo lub w lewo) w treści formuły – zaznaczając go. Można zatem łatwo zastąpić taki symbol swoim własnym wyrażeniem.

Symbole zastępcze są wstawiane do formuły przez szablony narzędzia „Elementy”. Nic nie stoi jednak na przeszkodzie aby autor samodzielnie wpisał ciąg <?> sygnalizujący miejsce późniejszego uzupełnienia formuły.

Wielkość formuły.

Wspomniałem już, że fizycznym rozmiarem formuły steruje wielkość zastosowanej czcionki ustalana poprzez polecenie „Format – Rozmiar czcionki” w pasku poleceń edytora równań. Pojawia się jednak pytanie, jak duża, w sensie liczby elementów składowych, może być formuła. Edytor nie ma tu formalnego ograniczenia, jednak nie potrafi automatycznie podzielić formuły na części, wtedy gdy jej długość przekracza szerokość przeznaczanego dla niej miejsca. W celu podzielenia formuły należy wykorzystać słowo kluczowe „newline”, które oznacza, że dalsza część zapisu pojawi się w nowej linii obszaru wizualizacji. Naciskanie klawisza ENTER w obszarze poleceń pozwala co prawda na wygodną prezentację poszczególnych części składowych formuły, nie ma jednak żadnego wpływu na jej postać wizualną. Dzieląc formułę należy pamiętać, że ostatnim znakiem w linii, która jest „przełamywana” nie może być znak żadnego operatora. Nie można na końcu takiej części formuły pozostawić np. znaku „+” albo „=”.

Podobnie do działania klawisza ENTER jest też z wykorzystaniem klawisza spacji, który pozwala rozdzielać poszczególne elementy formuły w obszarze poleceń, nie ma jednak wpływu na odstępy wstawiane w obszarze wizualizacji. Edytor umożliwia wykorzystanie dwóch słów kluczowych języka znaczników, jednego wstawiającego do formuły odstęp i drugiego wstawiającego mały odstęp. Te dwa słowa kluczowe to właściwie dwa symbole dostępne z klawiatury: znak akcentu „`” odpowiada za mały odstęp a znak tyldy „~” – za odstęp. Rolę tych słów kluczowych przedstawia ilustracja poniżej.

Słowa kluczowe „newline”, odstęp i mały odstęp można wprowadzić do formuły wykorzystując odpowiedni szablon w kategorii „Formaty” polecenia „Elementy”.

Na ilustracji widać, że pomimo wstawienia wielu spacji w zapisie ostatniego równania, nie przeniosły się one do obszaru wizualizacji. Poprzedzenie zapisu trzeciego równania słowem kluczowym „newline” spowodowało zapisanie go w nowej linii.

Tworzenie układów równań.

Jak widać polecenie „newline” pozwala nie tylko podzielić formułę, ale też umożliwi wprowadzenie układu równań. Jest jednak pewien problem. Użycie polecenia „newline” wyklucza możliwość skorzystania z ograniczników dopasowanych do wysokości układu. Nie można zatem tym sposobem uzyskać efektu pokazanego na rys. 22 powyżej. Aby to osiągnąć trzeba wstawić wielopoziomową strukturę formuły (a nie wiele poziomów struktury) a zrealizować to można za pomocą jednego ze słów kluczowych lub odpowiedniego szablonu. Stosowne szablony znajdują się we wspomnianej już kategorii „Formaty” i opisane w Apache OpenOffice jako „Stos pionowy (2 elementy)”, „Stos pionowy” i „Stos macierzy” a w LibreOffice jako: „Rozmieszczenie pionowe (2 elementy)”, „Rozmieszczenie pionowe” i „Rozmieszczenie macierzy”. Słowami kluczowymi wraz z wymaganą składnią odpowiadającymi tym szablonom są:

• binom {<?>} {<?>}
  To polecenie wymaga podania dwóch wyrażeń i ustawi je jedno nad drugim.

• stack {<?> # <?> # <?>}
  To polecenie pozwala utworzyć wielopoziomową strukturę wyrażeń. Wyrażenia poszczególnych poziomów, z wyjątkiem ostatniego, zakończone są znakiem „#”. Objęcie nawiasami grupującymi wyrażeń należących do zakresu słowa kluczowego „stack” jest obowiązkowe.

• matrix {<?> # <?> ## <?> # <?>}
  To polecenie pozwala utworzyć wielopoziomowy i wielokolumnowy układ formuł. Najczęściej wykorzystywane jest do tworzenia macierzy. Poszczególne elementy kolumny oddzielane są znakiem „#” natomiast cały wiersz zakończony jest dwoma znakami „##”. Także w tym zapisie nawiasy grupujące są obowiązkowe.

Ilustracja poniżej przedstawia sposób ułożenia dwóch równań tak aby znaki równości w tych równaniach się pokrywały. Widoczne w obszarze poleceń puste grupy, zapisane po znakach równości, mają na celu zapewnienie kompletności zapisu. Wspomniałem bowiem, że edytor równań zasygnalizuje błąd, gdyby formuła była formalnie niepoprawna, a więc gdy po znaku równości, plusa czy minusa nie pojawiłby się żaden wpis. Efekt uzyskany na ilustracji jest wynikiem dodatkowego ustawienia wyrównywania (Format – Wyrównanie...) na: „Do prawej”.

Jeśli autor uzna, że odstęp po znaku równości jest zbyt duży, może wykorzystać wspomniane już polecenie „Format – Odstępy...” i w kategorii „Macierze” zweryfikować odstęp między kolumnami.

Kontynuując temat układu równań wypada poruszyć jeszcze jeden aspekt. Jeśli prawe strony równań nie są jednakowej długości pojawi się nieestetyczny efekt dużej przerwy po znaku równości, gdyż wszystkie elementy są wyrównane do prawej strony. Składnia języka zawiera nieomówione jeszcze słowa kluczowe zmieniające sposób wyrównania jednego konkretnego elementu. Są trzy takie słowa: „alignl” wyrównujące do lewej strony, „alignc” - wyrównujące do środka oraz „alignr” wyrównujące do prawej strony. Mają one także swoje odzwierciedlenie w postaci szablonów kategorii „Format” zestawu „Elementy”. Poprzedzenie zapisów wprowadzonych do drugiej kolumny macierzy poleceniem „alignl” spowoduje, że równania mogą wyglądać tak, jak na poniższej ilustracji.

Ta ilustracja pokazuje także jak można w obszarze poleceń zapisać strukturalnie swoją formułę co pozwoli łatwiej ją modyfikować w razie potrzeby. Wpisanie w wierszu dwóch znaków procenta „%%” oznacza, że dalsza część tego wiersza będzie traktowana jako komentarz i nie ma wpływu na wygląd formuły. Dzięki temu można pozostawić opis tego, czego dotyczą poszczególne wpisy.

Przygotowałem taki szablon dla układu trzech równań i zapisałem w postaci pliku ODF. Szablon umieści równania w taki sposób, jaki przedstawia poniższy rysunek.

Można go pobrać stąd rownania_3_niewiadome.odf i wykorzystać do nauki, ćwiczeń czy do pracy.

Przypominam, że aby umieścić formułę w dokumencie Writera należy użyć polecenia „Wstaw – Obiekt – Obiekt OLE...”. Natomiast aby łatwo dotrzeć do symboli zastępczych, które trzeba zastąpić własnymi wyrażeniami warto korzystać z klawisza F4.

Dotychczasowy wydźwięk opracowania wskazuje, że o ile do tworzenia prostszych formuł wystarczy umiejętne wykorzystanie szablonów zawartych w poleceniach „Elementy”, to poznanie języka znaczników pozwoli na większą swobodę w konstruowaniu formuł.

Język znaczników.

Ta część opracowania nie pretenduje do miana podręcznika, ma jednak przybliżyć znajomość i znaczenie słów kluczowych. Większość tych słów użytkownik Writera pozna korzystając z szablonów. Jednak nie wszystkie możliwości są dostępne w szablonach. Niektóre jak np. możliwość kolorowania, zmiany rozmiaru lub ukrywania wybranych fragmentów formuł dostępne są w „Elementach” w kategorii „Atrybuty” tylko w LibreOffice a jeszcze inne nie występują w ogóle w postaci szablonów.

Mówiąc o „słowach kluczowych” w języku znaczników odnoszę się nie tylko do słów będących rzeczywiście wyrazami, ale także symboli, których użycie wpływa na wygląd formuły. Słowa kluczowe można wpisywać nie zwracając uwagi na wielkość liter, zatem zapisy „1 over 2”, „1 OVER 2” albo „1 oVeR 2” zostaną zawsze zinterpretowane w ten sam sposób.

Już wiadomo, że znaki nawiasów klamrowych wprowadzane z klawiatury oznaczają w języku znaczników grupowanie wyrażeń, a znaki akcentu, tyldy czy procenta mają swoje własne znaczenie w tworzonej formule. Edytor formuły rozpoznaje wprowadzane wyrażenia i wpisy, i te które nie odpowiadają słowom kluczowym interpretuje zgodnie z następującymi zasadami ogólnymi:

• Rozpoznane nazwy funkcji są prezentowane czcionką prostą, taką samą czcionką przedstawiane są liczby.
• Wpisy, które edytor uznaje za nazwy zmiennych przedstawiane są czcionką pochyłą.
• Jeśli autor formuły zechce do niej wprowadzić zwykły tekst to musi on być objęty cudzysłowami. Takie teksty są także prezentowane czcionką prostą.
• Wpisy rozpoczynające się od znaku % są traktowane jak nazwa symbolu i jeśli rzeczywiście odpowiadają jakiemuś symbolowi, zostanie on ukazany np. „%ialpha” pokaże w formule α, lecz już zapis „%ialfa” nie zostanie rozpoznany jako symbol i w formule pojawi się jako „%ialfa”.
• Wystąpienie dwóch kolejnych znaków % jest interpretowane przez edytor jako początek komentarza autorskiego wstawionego do formuły, w związku z czym cała treść aż do końca wiersza nie wpływa na samą formułę. Przykład widać na rys. 27.

Znakami będącymi jednocześnie słowami kluczowymi są: %, {, }, &, |, _, ^,~,`, i ". Znak „&” odpowiada słowu kluczowemu „and” natomiast znak „|” (pionowa kreska) odpowiada słowu kluczowemu „or”. Znak podkreślnika „_” odpowiada słowu kluczowemu „sub” i powoduje, że następny zapis jest traktowany jako indeks dolny. Znak daszka „^” odpowiada słowu kluczowemu „sup” i powoduje wstawienie dalszego zapisu jako indeksu górnego. O znakach akcentu i tyldy już napisałem. Znaków tych nie można wprowadzić bezpośrednio do wizualnej postaci formuły. Jeśli autor chciałby to zrobić, to ma dwie metody:

Po pierwsze może dodać potrzebny symbol do katalogu symboli.

Po drugie potrzebny symbol można zapisać w formule jako zwykły tekst ujmując go w parę cudzysłowów. Jedynym wyjątkiem jest tu sam znak cudzysłowu, który należy wpisać następująco: "\"" (cudzysłów, lewy ukośnik, cudzysłów, cudzysłów).

Z powodu wykorzystywania słów kluczowych w języku znaczników nie można także stosować jako wyrażeń wpisów zbieżnych z pisownią tych słów.

Wyrażenia indeksowane.

Napisałem już powyżej, że znaki podkreślnika i daszka pozwalają uzupełnić wyrażenie o odpowiedni indeks. Za dodanie indeksu odpowiadają także słowa kluczowe: „sup” (indeks górny) i „sub” (indeks dolny). Te słowa kluczowe w tej postaci dodają indeksy po prawej stronie wyrażenia i muszą być zapisane po wyrażeniu którego dotyczą. Jednak dla każdego z tych słów kluczowych istnieją dodatkowe trzy warianty decydujące czy indeks będzie położony po prawej stronie, po lewej czy nad (gdy dotyczy to indeksu górnego) albo pod wyrażeniem (gdy dotyczy indeksu dolnego). Te trzy warianty to wymienione już słowa kluczowe poprzedzone literą: „r” (prawy), „l” (lewy) lub „c” (centralny). A więc słowo kluczowe „csup” umieści indeks nad wyrażeniem a „lsub” u dołu po lewej stronie. Słowa kluczowe umieszczane są po wyrażeniu którego dotyczą w dowolnej kolejności. Przykładem użycia tej składni niech będzie przedstawienie symbolicznego zapisu pierwiastka Niob.

Symbol Nb i nazwa pierwiastka zostały ujęte w cudzysłowy aby zapis nie został przedstawiony pismem pochyłym.

Wyrażenia z granicami.

Wyrażenia z granicami to operatory, które mogą wskazywać zakres oddziaływania. Najbardziej znanymi są operatory sumowania, całkowania i granic funkcji albo ciągu. Jednak takich operatorów jest więcej i nie wszystkie występują na liście szablonów w kategorii „Operatory”.

W formułach operatory mogą występować samodzielnie, wyłącznie w postaci symbolu operatora z argumentem albo uzupełnione o granice i określające zakres ich działania. Dla wszystkich operatorów dopuszczalna jest składnia dodatkowo określająca dolny i górny zakres. Słowami kluczowymi odpowiadającymi za te wartości są: „from” (od) oraz „to” (do). „From” umieszcza należące do niego wyrażenie pod operatorem a „to” umieszcza wyrażenie nad operatorem. Kolejność tych słów kluczowych ani to czy występują oba nie ma znaczenia. Jeśli zakresy będą zastosowane, to muszą wystąpić po nazwie operatora a przed jego argumentem. Poniżej przedstawiam listę dostępnych operatorów. Znaki „+” w lewych kolumnach określają czy w wybranym pakiecie operator można wprowadzić do formuły za pomocą szablonu.

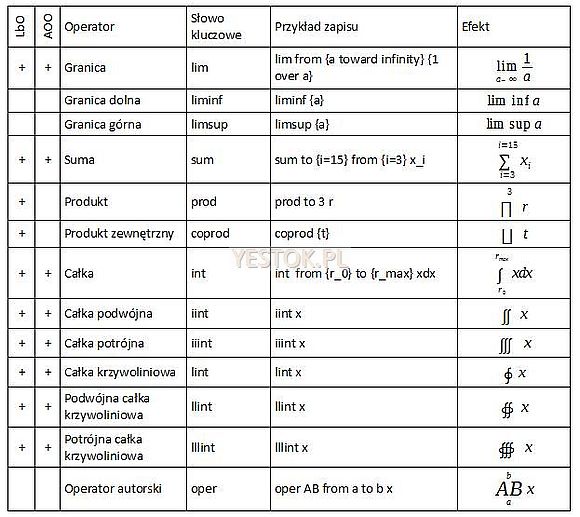
Na uwagę zasługuje ostatni z operatorów, nazwany przeze mnie operatorem autorskim. Pozwala on określić własny operator. Symbol albo nazwa tego operatora musi wystąpić po słowie kluczowym „oper”.

Funkcje.

Edytor równań rozpoznaje nazwy funkcji i zgodnie z zasadami konstruowania formuły wprowadza do niej ich nazwy pismem prostym. Pierwsze cztery funkcje nie mają prezentacji poprzez nazwę więc nie można o nich powiedzieć, że wstawiane są pismem prostym. Rozpoznawane są następujące funkcje:

abs {x} – wartość bezwzględna.

fact {x} – silnia (pismem prostym wstawiany jest znak !).

sqrt {x} – pierwiastek kwadratowy.

nroot {n} {x} – pierwiastek n-tego stopnia.

Poniższe funkcje, jeśli zostaną wprowadzone z szablonu elementów kategorii „Funkcje”, automatycznie umieszczą argument w nawiasach okrągłych.

ln {x} – logarytm naturalny.

log {x} – logarytm dziesiętny.

exp {x} – funkcja wykładnicza.

sin, cos, tan, cot – funkcje trygonometryczne: sinus, cosinus, tangens, cotangens.

sinh, cosh, tanh, coth – funkcje hiperboliczne: sinus hiperboliczny, cosinus hiperboliczny itd.

arcsin, arccos, arctan, arccot – funkcje cyklometryczne: arcus sinus, arcus cosinus itd.

Kolejne funkcje nie występują w elementach kategorii „Funkcje” Apache OpenOffice ale są w tym pakiecie rozpoznawane jako prawidłowe nazwy funkcji.

arsinh, arcosh, artanh, arcoth – funkcje hiperboliczne odwrotne: area sinus, area cosinus itd.

Ponadto występuje dodatkowo słowo kluczowe dla funkcji autorskich. Tym słowem jest „func”. Wyrażenie zapisane po tym słowie jest traktowane jak nazwa funkcji i wprowadzane do formuły pismem prostym. Dzięki temu można wprowadzić inne, niezdefiniowane nazwy funkcji, jak np. secans (sec) wpisując ciąg „func sec {x}”.

W szablonach funkcji dostępny jest szablon oznaczony jako e^x. W rzeczywistości wprowadza on do obszaru poleceń wpis „func e^{<?>}”. Litera „e” nie jest w tym wypadku nazwą funkcji lecz stałą (to liczba Eulera) a stałe do formuł należy także wprowadzać pismem prostym.

Atrybuty.

Wyrażenia stosowane w formułach można opatrzyć atrybutami i dzięki temu zmienić ich wygląd. Można uzupełnić wyrażenia o strzałki, kreski, kropki i inne symbole umieszczane nad, pod lub w poprzek wyrażenia. Atrybutom przypisane są słowa kluczowe które należy umieszczać przed wyrażeniem którego mają dotyczyć. Szablony atrybutów są dostępne w kategorii „Atrybuty” polecenia „Elementy”. W wydaniu LibreOffice udostępniono więcej atrybutów niż w Apache OpenOffice dlatego omówię te, które nie występują w Apache OpenOffice oraz te, których nie pokazano w żadnej wersji. Oto te słowa kluczowe:

„size” – to słowo kluczowe zmienia wielkość zastosowanej czcionki w następującym po nim wyrażeniu. To także dzięki temu można zmienić fizyczny rozmiar obszaru wizualizacji. Składnia tego słowa kluczowego wymaga podania dwóch elementów. Pierwszy określa wielkość czcionki, drugi jest wyrażeniem którego ta wielkość dotyczy. Pierwszy element może być:

• Liczbą określającą wymaganą wielkość czcionki np. „size 36 {a}” oznacza że wyrażenie „a” ma być wstawione czcionką o wielkości 36 pkt.
• Liczbą określającą współczynnik zmiany wielkości w stosunku do używanej czcionki. Wartość współczynnika wpisywana jest po znaku gwiazdki, np. „size *2.5 {a}” oznacza, że wyrażenie „a” ma być wstawione czcionką 2,5 razy większą niż czcionka podstawowa. UWAGA! Separatorem części ułamkowej jest w tym zapisie znak kropki.
• Liczbą określającą bezwzględną zmianę czcionki o określoną ilość punktów, np. „size +10 {a}” oznacza, że wyrażenie „a” ma być wstawione czcionką o 10 pkt większą od czcionki podstawowej. Podanie liczby ze znakiem minus oznacza, że ma zostać użyta mniejsza czcionka

„color” – to słowo kluczowe zmienia kolor czcionki w wyrażeniu którego dotyczy. Jeśli wyrażenie nie będzie objęte nawiasami grupującymi, to po pierwszej napotkanej spacji, następne wyrażenie będzie w kolorze podstawowym. Składnia tego słowa kluczowego wymaga podania nazwy koloru a następnie wyrażenia. Dopuszczalnymi nazwami kolorów są: black, blue, cyan, green, magenta, red, white i yellow. Kolorów: gray, lime, maroon, navy, olive, purple, silver i teal można użyć tylko w wersji LibreOffice.

Kolorowanie formuły jest jednak nieco bardziej złożone i kierowanie się zasadą „pierwszej spacji” może być zwodnicze. Najlepiej zobrazuje to poniższa ilustracja pokazująca tę samą formułę kolorowaną w różny sposób.

Obok każdej formuły podaję jej zapis w języku znaczników. Jak to widać w ostatnim przykładzie także znak plusa jest ogranicznikiem zakresu kolorowania.

„bold” – to słowo kluczowe nadaje czcionkom atrybut pogrubienia. Zasady oddziaływania są takie same jak dla wspomnianego powyżej „color”.

„ital” i równoważnie „italic” – to słowa kluczowe nadające następującemu po nim wyrażeniu atrybut pisma pochylonego. Tylko tym atrybutem można zmienić wprowadzony do formuły tekst ujęty w cudzysłowy na pochylony.

„font” – to słowo kluczowe zmienia czcionkę następującego po nim wyrażenia. Składnia tego słowa wymaga podania rodzaju czcionki jaki ma zostać zastosowany. Po słowie kluczowym musi wystąpić jedno ze słów: „serif”, „sans” lub „fixed”. „Serif” oznacza czcionkę szeryfową, czyli z charakterystycznymi zakończeniami liter. „Sans” – czcionkę bezszeryfową, w której litery mają proste zakończenia. „Fixed” – oznacza czcionkę nieproporcjonalną, czyli taką, w której każda litera zajmuje taką samą przestrzeń. O tym jakie to są konkretnie czcionki decyduje ustawienie parametru „Czcionki niestandardowe” w oknie dialogowym „Czcionki” pokazanym na rys. 16.

„phantom” – to słowo kluczowe powoduje, że objęte nim wyrażenie zajmując miejsce nie jest pokazywane w formule. Często jest wykorzystywane do pozostawienia pustego miejsca w formule w celu np. wyrównania położenia wyrażeń.

„nbold” – to słowo odwołuje atrybut pogrubienia czcionki.

„nitalic” – to słowo odwołuje atrybut pochylenia czcionki.

Dwa ostatnie słowa kluczowe nie mają swojego odpowiednika w zestawie atrybutów w narzędziach „Elementy” zestawu LibreOffice.

Inne słowa kluczowe.

„newline” – słowo to powoduje, że następna część formuły pojawi się w nowej linii. Wystąpiło już tyle razy w cytowanych przykładach, że jego znaczenie jest oczywiste.

„nospace” – słowo kluczowe likwiduje odstępy wstawiane między wyrażenia. Kiedy w obszarze poleceń wstawiony zostanie ciąg w rodzaju „{a b c}” edytor ustawi te litery w obszarze wizualizacji z pewnymi odstępami, zapis tego ciągu w postaci „nospace {a b c}” zredukuje odstępy między literami.

„infinity” albo „infty” – to słowo kluczowe wstawia symbol nieskończoności.

„partial” – to słowo kluczowe wstawia symbol pochodnej cząstkowej.

Poniżej w tabelarycznym zestawieniu przedstawiam wybrane słowa kluczowe języka znaczników i ich wizualną postać dla obu wersji pakietu (x)Office. Każdy przykład odniosłem do wersji pakietu i przypisałem mu „+” albo „–” mówiący o tym czy ten zapis jest w ogóle dostępny w tej wersji, czy może zostać pobrany z szablonu polecenia „Elementy” i czy znajduje się na liście podręcznego menu obszaru poleceń.

Zapis w obszarze poleceń	Obszar wizualizacji	LBO			AOO
		Dostępne	Szablon	Menu	Dostępne	Szablon	Menu
Zapis w obszarze poleceń	Obszar wizualizacji	Dostępne	Szablon	Menu	Dostępne	Szablon	Menu
		LBO			AOO
+a		+	+	+	+	+	+
-a		+	+	+	+	+	+
+-a		+	+	+	+	+	+
-+a		+	+	+	+	+	+
a+b		+	+	+	+	+	+
a-b		+	+	+	+	+	+
a cdot b		+	+	+	+	+	+
a times b		+	+	+	+	+	+
a * b		+	+	+	+	+	+
a over b		+	+	+	+	+	+
a div b		+	+	+	+	+	+
a/b		+	+	+	+	+	+
a circ b		+	+	+	+	+	+
a wideslash b		+	+	+	+	–	+
a widebslash b		+	+	+	+	–	+
neg a		+	+	+	+	+	+
a and b		+	+	+	+	+	+
a or b		+	+	+	+	+	+
a otimes b		+	+	–	+	–	–
a=b		+	+	+	+	+	+
a <> b		+	+	+	+	+	+
a < b		+	+	+	+	+	+
a <= b		+	+	+	+	+	+
a leslant b		+	+	+	+	+	+
a > b		+	+	+	+	+	+
a >= b		+	+	+	+	+	+
a geslant b		+	+	+	+	+	+
a approx b		+	+	+	+	+	+
a sim b		+	+	+	+	+	+
a simeq b		+	+	+	+	+	+
a equiv b		+	+	+	+	+	+
a prop b		+	+	+	+	+	+
a parallel b		+	+	+	+	+	+
a ortho b		+	+	+	+	+	+
a divides b		+	+	+	+	+	+
a ndivides b		+	+	+	+	+	+
a toward b		+	+	+	+	+	+
a dlarrow b		+	+	+	+	–	+
a dlrarrow b		+	+	+	+	–	+
a drarrow b		+	+	+	+	–	+
a prec b		+	+	+	–	–	–
a succ b		+	+	+	–	–	–
a preccurlyeq b		+	+	+	–	–	–
a succcurlyeq b		+	+	+	–	–	–
a precsim b		+	+	+	–	–	–
a succsim b		+	+	+	–	–	–
a nprec b		+	+	+	–	–	–
a nsucc b		+	+	+	–	–	–
a >> b		+	–	–	+	–	–
a << b		+	–	–	+	–	–
a in A		+	+	+	+	+	+
a notin A		+	+	+	+	+	+
A owns a		+	+	+	+	+	+
A setminus B		+	+	+	+	+	+
A slash B		+	+	+	+	+	+
A subset B		+	+	+	+	+	+
A supset B		+	+	+	+	+	+
A supseteq B		+	+	+	+	+	+
A nsubset B		+	+	+	+	+	+
A nsupset B		+	+	+	+	+	+
A nsupseq B		+	+	+	+	+	+
emptyset		+	+	+	+	+	+
aleph		+	+	+	+	+	+
SetC		+	+	+	+	–	+
SetN		+	+	+	+	–	+
SetR		+	+	+	+	–	+
SetQ		+	+	+	+	–	+
SetZ		+	+	+	+	–	+
notexists		+	+	+	–	–	–
backepsilon		+	–	–	+	–	–

Tym, którzy chcieliby poczytać więcej na temat tworzenia formuł załączam do pobrania podręcznik (w języku angielskim) „Math Guide – Using the Equation Editor”. Plik jest w formacie PDF (ok. 2 MB).

Aby pobrać podręcznik kliknij link: lbo mg40-mathguide.pdf

Wstawianie równań z ich automatycznym numerowaniem.

Jedną z pożądanych cech opracowań zawierających wzory i formuły obliczeniowe jest ich numerowanie, szczególnie wówczas gdy takich obiektów jest wiele i gdy autor chce się do nich odwoływać w treści opracowania. Dobrze jest gdy numeracja spełnia dwa ważne warunki:

• Powstaje automatycznie podczas wstawiania formuły.
• Można się do niej odwołać poprzez mechanizm wstawiania odwołania. Można dzięki temu wstawić w treści opracowania wyrażenie w rodzaju: „mówi o tym wzór xxx na stronie yyy”, w którym zarówno „xxx” jak i „yyy” nie zależą od tego czy wzór został przeniesiony w inne miejsce albo czy przed nim wstawiono inne wzory.

Przyjęło się, że numeracja formuł umieszczana jest po prawej stronie formuły a takiego sposobu numerowania nie „obsługuje” żaden z podpisów możliwych do zastosowania w dokumencie. Jest to właściwie pięta achillesowa wielu edytorów i znajduje rozwiązanie dopiero w zaawansowanych i dedykowanych takim zagadnieniom programach. Autorzy (x)Office zaimplementowali rozwiązanie wykorzystywane także w innych programach edytorskich.

Bazuje ono na wykorzystaniu tabeli, jako elementu, w którym wstawiana jest formuła. W (x)Office wykorzystano tabelę zawierającą jeden wiersz z dwoma kolumnami. Tabela automatycznie zajmuje całą szerokość strony od lewego do prawego marginesu. Pierwsza kolumna zajmuje 89% szerokości a druga 11%. W pierwszej kolumnie zawartość wyrównana jest do środka zarówno w poziomie jak i w pionie, dzięki czemu wszystko co znajdzie się w tej kolumnie (i zarazem komórce tabeli) zostanie umieszczone na środku. Ta komórka jest przeznaczona na wstawienie formuły. Druga, wąska kolumna, jest wyrównana do prawej w poziomie i do środka w pionie. Ta kolumna (i zarazem komórka) przeznaczona jest na wprowadzenie numeru równania. Numer równania generuje pole „Sekwencja” z nazwą „Tekst”. Pole to należy do kategorii „Zmienne”. Takie pole ujawnia się w dokumencie jako numer kolejnego wystąpienia pola z konkretną nazwą, licząc te wystąpienia od początku dokumentu. Dlatego, bez względu na kolejność wstawiania pól są one zawsze ponumerowane rosnąco. Co za tym idzie wstawiane formuły będą zawsze prawidłowo ponumerowane.

Nazwa „Tekst” może zostać wykorzystana jako typ tworzonego odsyłacza. Dzięki temu można powołując się na formułę wskazywać jej numer, stronę na której się znajduje czy określenie „powyżej/poniżej” a stosowne wartości będą zawsze pobrane automatycznie. O odsyłaczach napisałem oddzielne opracowanie. Zainteresowanych odsyłam do opracowania „Zakładki, hiperłącza i odsyłacze”.

Cały mechanizm utworzenia tabeli z numerem i formułą umieszczono jako strukturę autotekstu co pozwala łatwo ją przywołać. Aby z niego skorzystać wystarczy wpisać dwie litery: „fn” i nacisnąć klawisz funkcyjny F3. Można także zacząć wpisywać wyraz „numeracja”. Już po pierwszych trzech wpisanych literach pojawi się charakterystyczny „dymek” z napisem „Numeracja formuł”. Widać go na ilustracji poniżej.

Jest to sygnał, że do wpisanego ciągu liter pasuje pozycja autotekstu. Wystarczy w tej sytuacji przerwać pisanie i nacisnąć klawisz ENTER. W obu przypadkach nastąpi wstawienie omówionej tabeli. Aby autor wiedział gdzie jest formuła, w tabeli znajduje się już wpisana formuła równania Einsteina.

Oto przykład takiej tabeli.

Ten mechanizm można oczywiście wykorzystać z dowolnymi elementami umieszczonymi w pierwszej komórce tabeli. Numer kolejny nie rachuje przecież faktycznie wstawionej formuły lecz kolejne wystąpienie pola „Sekwencja”. W komórce tabeli może więc znajdować się obrazek graficzny formuły utworzony w innym edytorze formuł.

Na zakończenie chciałbym przedstawić zmodyfikowane przeze mnie rozwiązanie numerowania formuł:

Tabela zawierająca formułę składa się z trzech komórek w jednym wierszu. Skrajne komórki zajmują po 10% szerokości tabeli, natomiast komórka środkowa 80%. Pozostałe ustawienia właściwości komórek i tabeli nie ulegają zmianie. Jednak dzięki temu zabiegowi formuła będzie się teraz znajdowała dokładnie w środku między lewym a prawym marginesem strony.

Pole „Sekwencja” znajdujące się w prawej komórce odwołuje się do nazwy „Równanie” i ma ustawiony parametr „Numeracja według rozdziałów” na wartość 1 (w tabeli „FN” ten parametr jest ustawiony na „Brak”) a separator na znak kropki. Dzięki takiej konstrukcji numerowanie formuł zmienia się gdy opracowanie zostało skonstruowane zgodnie z zasadami konspektu, to znaczy rozdziały główne i podrzędne mają przypisane style „Nagłówek 1”, „Nagłówek 2” itd. Gdy tak jest, numeracja formuł rozpoczyna się od wartości 1 w każdym rozdziale rozpoczętym tytułem o stylu „Nagłówek 1”.

Jeżeli autor włączy numerowanie konspektu, i każdy tytuł zostanie automatycznie poprzedzony kolejnym numerem rozdziału lub innym wyróżnikiem (mogą to być liczby rzymskie albo oznaczenia literami alfabetu), to numerowanie formuł przyjmie postać „Numer rozdziału – kropka – kolejny numer formuły w rozdziale”. Można więc uzyskać taki efekt: (1.1), (1.2), (1.3) itd. dla formuł w rozdziale pierwszym, (2.1), (2.2), (2.3)... w drugim i tak dalej dla każdego kolejnego rozdziału. Pierwszym elementem numeru równania będzie to, co zostanie wybrane jako numerowanie rozdziałów w konspekcie, a więc liczba, litery alfabetu albo liczby rzymskie. Odsyłacze do równań wstawianych do dokumentu tym nowym sposobem należy konstruować powołując się na typ „Równanie”.

Tabelę zawierającą taki sposób wstawiania numerowanych formuł umieściłem w pliku „numerowanie_formul.odt”, który można pobrać stąd: numerowanie_formul.odt

Po otwarciu pliku można zaznaczyć całą jego zawartość a następnie dodać ją jako autotekst do własnego wydania pakietu (x)Office, nadając mu swoją nazwę i skrót. Na własne potrzeby nadałem nazwę „Nowy numer formuły” i skrót „NNF”. O autotekście istnieje oddzielne opracowanie, które można przeczytać klikając tutaj. Tabelę tę można także dodawać do dokumentu bezpośrednio z pliku. Należy wówczas we własnej pracy skorzystać z polecenia „Wstaw – Dokument...”