Yestok.pl

W drugiej części opracowania zajmę się problemem prezentacji wartości komórek i budowaniem formuł obliczeniowych.

Prezentacja wartości w komórkach.

W komórce zawsze znajduje się wartość do niej wstawiona, lub w niej wyliczona. Jest to więc ciąg znakowy, wartość logiczna lub wartość liczbowa. Każdą wartość liczbową można przedstawić w arkuszu w żądany sposób i nazywamy to formatowaniem komórki. Komórki można formatować pojedynczo ale także grupowo, zaznaczając najpierw w arkuszu obszar, w którym komórki mają wyglądać podobnie. Na ilustracji poniżej przedstawiony jest ponownie arkusz Google. Zaznaczyłem na niej umiejscowienie opcji odpowiedzialnych za prezentację zawartości komórek.

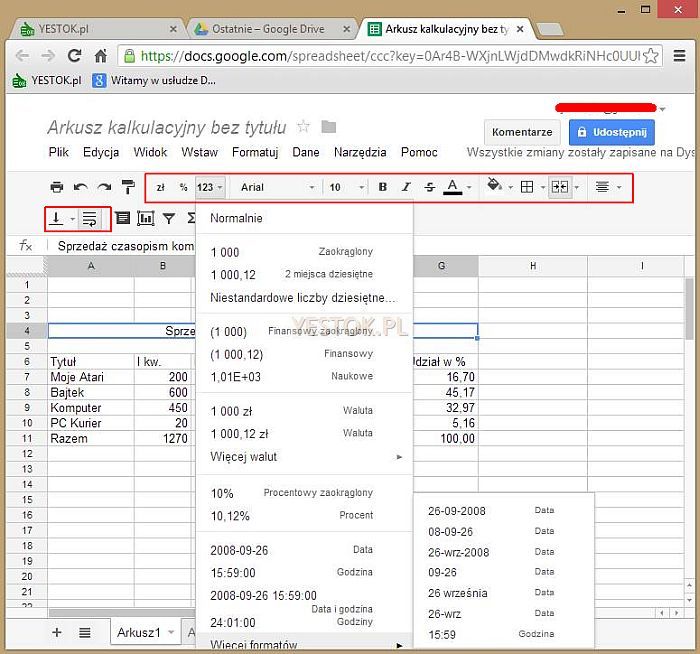
Każdy symbol w tym zaznaczonym obszarze oznacza przypisanie do komórki pewnej właściwości. Niektóre symbole mają przy prawej krawędzi znaczek małego trójkąta z wierzchołkiem skierowanym w dół. Kliknięcie tego trójkąta spowoduje rozwinięcie dłuższej listy dostępnych możliwości. Tak jest w przypadku rozwinięcia takiej listy przypisanej do symbolu „123”. Ta rozwinięta lista przedstawia rozbudowane możliwości prezentowania liczby znajdującej się w komórce. Jeszcze raz przypomnę, że wartość znajdująca się w komórce nie zmienia się przez przypisanie jej formatowania. Dodam także, że przypisanie sposobu prezentowania liczb nie jest związane z aktualną zawartością komórki. Można przypisać sposób prezentowania liczby do komórki, w której jest tekst albo która jest pusta. Kiedy w komórce pojawi się liczba, wtedy zostanie przedstawiona według zadanego formatu.

Oto omówienie poszczególnych sposobów formatowania.

Normalnie – oznacza, że nie przypisuje się żadnej właściwości do prezentowania liczby, zatem zostanie ona wyświetlona tak, jak uzna arkusz kalkulacyjny.

1 000 Zaokrąglony – oznacza, że liczba ma zostać wyświetlona jako liczba całkowita. Jeśli liczba byłaby tak duża, że zawierałaby grupy cyfrowe tysięcy, milionów i dalsze, to będą one oddzielone od siebie znakiem spacji. Liczba będzie wyświetlona jako zaokrąglona choć w komórce znajdować się będzie pierwotna wartość. Gdyby w komórce znajdowała się wartość 2345,67, to ten sposób formatowania wyświetli ją jako 2 346, odseparuje tysiące od pozostałej części i zaokrągli do liczby całkowitej.

1 000,12 2 miejsca dziesiętne – każda liczba ma zostać wyświetlona z dwoma miejscami po przecinku. Jeśli liczba nie ma tylu miejsc po przecinku, to brakujące pozycje zostaną uzupełnione zerami. Jeśli liczba ma więcej niż dwa miejsca po przecinku, to pozycja setnych części zostanie zaokrąglona zależnie od cyfry znajdującej się na pozycji tysięcznych.

Niestandardowe liczby dziesiętne – wybór tej opcji spowoduje pytanie, ile miejsc dziesiętnych po przecinku chcemy prezentować w liczbie? Można wybrać wartość od 0 do 10.

Finansowy – ten sposób prezentacji liczb jest analogiczny z wspomnianymi powyżej „2 miejsca dziesiętne”. W formatowaniu finansowym charakterystyczne jest to, że liczby ujemne przedstawiane są w nawiasach. Szczerze mówiąc chyba nigdy jak dotąd nie spotkałem się ze stosowaniem tego formatu w systemach księgowych.

1,01E+03 Naukowe – przedstawia każdą liczbę w notacji naukowej. W Google Docs ma ona dwa miejsca po przecinku, w Excelu i Calcu można samemu zdecydować o ilości tych miejsc.

Walutowa – przedstawia liczbę z dopisaniem do niej symbolu waluty polskiej (zł) lub wybranej z listy „Więcej walut”. Symbol waluty dopisywany jest w miejscu charakterystycznym dla danego kraju, dlatego np. będzie „100 zł” ale „$ 100”. Jeśli liczba jest ujemna to minus jest pierwszym znakiem, a więc np. „-$ 100”.

Procentowy – ten sposób prezentacji liczby, na potrzeby jej wyświetlenia mnoży ją wewnętrznie przez 100 i dopisuje znak „%”. Zatem wartość wpisana jako 0,01 zostanie wyświetlona jako 1% ale we wszystkich działaniach stosowana jest jej wartość 0,01.

Pozostałe formaty dotyczą przedstawienia liczby jako daty, godziny lub daty i godziny a ich opis jednoznacznie pokazuje jak liczba będzie prezentowana w komórce.

Wpisanie do komórki wartości zgodnie z którymś z wymienionych formatowań, spowoduje zaakceptowanie takiej liczby i automatyczne przypisanie komórce odpowiedniego formatowania. Wprowadzenie zatem do komórki wpisu „12%” spowoduje wprowadzenie do komórki wartości 0,12 z jednoczesną zmianą formatowania komórki na format „Procent”. Wpisanie ciągu”12-06-2012” zostanie zinterpretowane jako data i zostanie wyliczona odpowiednia liczba daty. Format komórki zostanie zmieniony na prezentację daty, w efekcie widziana w komórce zawartość będzie miała postać „2012-06-12”.

Na lewo od prezentowanej rozwiniętej listy formatowań znajdują się dwa symbole „zł” przypisujący format walutowy z dwoma miejscami po przecinku i „%”, przypisujący format procentowy, także z dwoma miejscami po przecinku. Jeśli więc któryś z tych formatów jest potrzebny, nie trzeba rozwijać pełnej, omówionej wcześniej, listy wyboru.

Pozostałe opcje formatowania zakreślone ramką, decydują o innych właściwościach przypisanych do komórki lub komórek. Rozwijana lista sygnowana na ilustracji napisem „Arial”, pozwala – po jej rozwinięciu – wybrać krój czcionki jaki zostanie zastosowany. Lista sygnowana liczbą „10”, po rozwinięciu pozwala wybrać wielkość czcionki, a kolejne cztery, przypisać czcionkom stosowne atrybuty: atrybut pogrubienia, pochylenia, przekreślenia i koloru.

Użytkownik arkusza naprowadzając wskaźnik myszki na wybraną opcję, uzyska podpowiedź wyjaśniającą jaka czynność może zostać zrealizowana. Kolejny przycisk,symbol kadzi z farbą, pozwala wybrać kolor tła komórki. Symbol wyglądem przypominający okno, pozwala wybrać jakie krawędzie zaznaczonego obszaru (lub komórki) mają zostać zaznaczone, jakiego mają być koloru i jaki zostanie zastosowany rodzaj linii.

Kolejna opcja pozwala scalać lub rozdzielać komórki. Żeby móc komórki scalać, należy najpierw zaznaczyć komórki przeznaczone do połączenia, w przeciwnym razie opcja ta będzie niedostępna. Rozdzielić można tylko komórki wcześniej scalone, więc najpierw trzeba uaktywnić komórkę scaloną a dopiero potem wykorzystać opcję rozdzielania. Na ilustracji, jak widać, ikonka tego przycisku jest aktywna, gdyż aktywną komórką jest akurat komórka scalona.

Ważne i często stosowane są dwie następne opcje. Pierwsza pozwala ustalić poziome położenie wpisów w komórce. Do wyboru jest wyrównanie do lewej krawędzi, do prawej i na środku, między krawędziami. Dotyczy to wszystkich wpisów i zmienia ich wyrównanie zastosowane domyślnie. Można więc dosunąć liczby do lewej krawędzi lub teksty do prawej co nie jest wszak ich naturalnym wyrównaniem. Kolejny symbol dotyczy wyrównania wpisów w stosunku do dolnej i górnej krawędzi komórek. Zawartość komórki może być wyświetlona przy górnej krawędzi, przy dolnej albo pośrodku, między krawędzią górną i dolną. Ma to znaczenie gdy wysokość komórki jest znacznie większa niż wysokość wpisu w komórce.

Ostatnia z zaznaczonych opcji, włącza lub wyłącza w komórce zgodę na zawijanie tekstu jeśli jest za długi w stosunku do szerokości komórki. Standardowo arkusze Google dla wszystkich komórek nowego arkusza ustawiają ten atrybut na: „zgoda na zawijanie”. Pamiętajmy, że zmiana atrybutu (wyłączenie go) dotyczyć będzie komórki aktywnej lub komórek zaznaczonych a nie wszystkich komórek w arkuszu. Atrybut ten dotyczy jednak tylko tekstów. Uwaga, w nowej wersji Arkuszy Google zmieniono zasady i ujednolicono je z zasadami obowiązującymi dotychczas w Excelu i Calcu. Zawijanie tekstu nie jest w nich teraz standardowym działaniem a tekst dłuższy niż szerokość komórki będzie wyświetlany poza nią tak daleko, dopóki komórki sąsiadujące będą puste.[dodane w listopadzie 2014] Na ilustracji poniżej przedstawiam cztery przykłady wprowadzenia tego samego tekstu – „Kabaretowy klub dwójki” – do komórek arkusza.

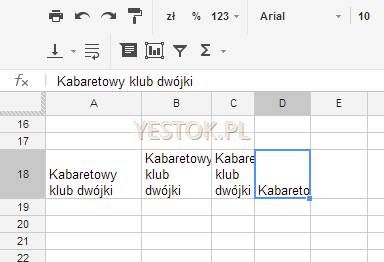
Wszystkie wpisy zostały dokonane w wierszu 18. Początkowo miał on standardową wysokość, taką jak widać w wierszu 17. czy 19. Wpis dokonany do komórki A18 był za długi, arkusz Google zawinął więc tekst tak, jak na to pozwoliła szerokość tej kolumny. Pozwoliła zaś wyświetlić w całości wyraz „Kabaretowy” i po zawinięciu, pozostałe dwa wyrazy. Wysokość wiersza została powiększona aby tekst był w całości widoczny. Ten sam tekst w komórce B18, ze względu na jej szerokość, musiał zostać zawinięty dwa razy, więc wysokość wiersza powiększyła się ponownie. W komórce C18, jeszcze węższej, mimo podwójnego zawinięcia, wyraz „Kabaretowy” nie mieści się w całości w jej szerokości, więc widoczne jest tylko tyle liter tego słowa, ile arkusz Google może wyświetlić. W ostatniej komórce, D18, wyłączona została opcja zawijania tekstu. Dlatego, mimo że tekst znajduje się w tej komórce w całości, widać to w wierszu wprowadzania, to wyświetlonych jest tylko tyle znaków, ile można zmieścić w szerokości komórki.

Analogiczne opcje formatowania komórek znajdują się także w Excelu i Calcu. W tych programach kliknięcie prawym przyciskiem myszy na wybranej komórce lub zaznaczonym obszarze, wyświetli menu kontekstowe, w którym jedna z opcji nazywa się „Formatuj komórki…”. Otwiera ona cały szereg możliwości formatowania.

Formuła.

Formuła to wpisana do komórki reguła podająca sposób wyznaczenia wyświetlanej w tej komórce informacji. We wszystkich arkuszach kalkulacyjnych formuła rozpoczyna się znakiem „=”, po którym musi wystąpić wpis zgodny z zasadami tworzenia wyrażeń. Jeśli wprowadzony zapis nie będzie odpowiadał poprawnie zbudowanej formule, pojawi się sygnalizacja błędu.

Wyróżnię cztery rodzaje formuł.

• Formułę arytmetyczną, czyli taką która da w wyniku obliczeń arytmetycznych liczbę.
• Formułę tekstową, czyli taką która da w wyniku przekształceń tekst.
• Formułę logiczną, czyli taką która da wyniku obliczeń logicznych wartość PRAWDA albo FAŁSZ.
• Formułę mieszaną, której wynikiem może być każdy z poprzednio wymienionych elementów.

Formuły arytmetyczne.

Rozważania o formułach rozpocznę od formuły arytmetycznej. Większości czytelników formuła kojarzy się właśnie z taką formą obliczeniową. Formuła składać się może z liczb wpisanych bezpośrednio do formuły, adresów komórek i funkcji, przy czym jeśli ma więcej niż jeden z wymienionych elementów, to muszą one być powiązane między sobą operatorami arytmetycznymi, a taki zapis nazywamy wyrażeniem arytmetycznym. Adresy komórek wskazują skąd do wyliczenia formuły ma być pobrana następna wartość. Inaczej mówiąc, nie podajemy liczby lecz podajemy miejsce gdzie ta liczba jest. To oznacza jednocześnie, że jeśli zmienimy zawartość komórki, której adres został podany w formule, zmieni się także wynik obliczony formułą.

Funkcje są algorytmami obliczeniowymi przygotowanymi przez twórców oprogramowania, ułatwiającymi wykonanie złożonych obliczeń. Funkcjom przypisano nazwy, i zdefiniowano argumenty, pozwalające wskazać wartości, jakie powinny uwzględnić w swoich obliczeniach. Jeśli w formułach użyto także funkcji, to ich wartości są obliczane przed innymi obliczeniami.

Operatory arytmetyczne to:

• potęgowanie – oznaczane znakiem „^” (daszek) ;
• Mnożenie – oznaczane znakiem „*” (gwiazdka);
• Dzielenie – oznaczane znakiem „/” (ukośnik);
• Dodawanie – oznaczane znakiem „+” (plus)
• i odejmowanie – oznaczane znakiem „-” (minus)

Najprostsza formuła arytmetyczna mogłaby zatem mieć postać „=7” lub „=E4”. Taki zapis nie wymaga żadnych obliczeń i w pierwszym przypadku wyświetli w komórce liczbę „7”, czyli będzie tym samym co wpisanie do komórki liczby 7. Drugi zapis oznacza żądanie wyświetlenia w komórce takiej wartości, jaka jest aktualnie wyznaczona w komórce „E4”.

Przyjrzyjmy się przykładowej formule: „=3+2*5^2-4+2/4”. Wartością wyświetloną w komórce będzie 49,5. Przy obliczaniu formuły uwzględnia się hierarchię obliczeń, w której na pierwszym miejscu jest potęgowanie, potem równorzędnie dzielenie i mnożenie i ostatecznie – także równorzędnie – dodawanie i odejmowanie, a samą formułę analizuje się od lewej strony do prawej. W powyższym przykładzie zostanie zatem najpierw obliczone potęgowanie „5²” czyli 25, następnie mnożenie 2×25 co da w wyniku 50 i dzielenie „2/4” co da w wyniku 0,5, ostatecznie sumowanie 3+50-4+0,5 da wynik 49,5.

Sposób obliczania można zmienić używając nawiasów. Hierarchia obliczeń nadal jest zachowana, ale najpierw zgodnie z nią wyliczone zostaną wartości w nawiasach. Dodanie nawiasów w przytoczonym przykładzie zmieni sposób obliczania, a więc i wynik. Niech formuła wygląda teraz tak „=(3+2)*(5^2-4)+2/4”. Obliczona wartość pierwszego nawiasu to 5. Drugi nawias zgodnie z kolejnością obliczeń to 21, a ostateczna wartość formuły to 5×21+0,5 czyli 105,5.

Jeśli obliczenia miałyby być jeszcze bardziej skomplikowane, można użyć kolejnych nawiasów, zagnieżdżonych wewnątrz innych. W arkuszach kalkulacyjnych zawsze są to nawiasy okrągłe i każdy nawias otwierający musi mieć „sparowany z nim” nawias zamykający. W tak złożonej strukturze najpierw wyliczane są wartości nawiasów najbardziej zagłębionych. Zatem formuła, w której nawiasy byłyby rozmieszczone tak „=(3+2)*(5^(2-4)+2)/4” wyznaczyłaby jeszcze inną wartość. Najbardziej wewnętrzne nawiasy wyliczają wartość 2-4 czyli -2 (minus 2). Wartość w pierwszych nawiasach to nadal 5. Wartość w drugiej parze nawiasów to 2,04 (5^-2 to – dla tych, którzy zapomnieli już o arytmetyce – jedna dwudziesta piąta, czyli 0,04). A cała wartość tego wyrażenia to ostatecznie 5×2,04/4 czyli, 2,55.

W miejscu każdej z liczb, w tych zaprezentowanych formułach, mógłby występować adres komórki, dzięki czemu formuły obliczałyby swą wartość na podstawie wartości z tych komórek.

Systemy sprawdzania poprawności konstruowanych formuł w arkuszach kalkulacyjnych wykrywają braki w domykaniu nawiasów i uzupełniają je automatycznie lub proponują sposób domknięcia.

Formuła tekstowa.

Formuła tekstowa składa się z tekstów podanych bezpośrednio, adresów komórek i funkcji. Jeśli wystąpi w takiej formule więcej niż jeden z wymienionych składników to muszą one być połączone operatorem działań tekstowych a wynikiem wykonania takiej formuły jest zawsze tekst. Jest tylko jeden operator działania na tekście, oznaczony znakiem „&” (ampersand). Oznacza on połączenie tekstów w jedną całość, możemy powiedzieć – dodaje teksty. Teksty bezpośrednio podane w formułach muszą być objęte cudzysłowami. W tej sytuacji zapis np. „="Pan "&B3&" "&C3” wyświetliłby w komórce treść „Pan Jan Kowal” gdyby w komórce B3 znajdował się wpis „Jan” a w C3 „Kowal”. Przykładowa formuła składa się z dwóch tekstów wpisanych bezpośrednio do niej i adresów dwóch komórek. Pierwszy tekst został podany ze znakiem spacji na końcu (po słowie Pan jest jeszcze spacja), drugi tekst, ujęty w cudzysłowy, składa się tylko ze spacji. Formułę zbudowano tak dlatego, by przed imieniem oraz między imieniem a nazwiskiem wystąpił odstęp. W przeciwnym razie prezentowana treść mogłaby wyglądać tak: „PanJanKowal”.

Formuła logiczna.

Formuła logiczna to specyficzny rodzaj formuły, szczególnie dla tych którzy z tą tematyką stykają się po raz pierwszy. Formuła tego typu przyjmuje w wyniku tylko jedną z dwóch wartości. Wartość PRAWDA albo wartość FAŁSZ. A skoro posługuję się tu arkuszem kalkulacyjnym Google Docs to wartości te noszą tu nazwę odpowiednio TRUE i FALSE. Tego typu formuła może składać się z liczb, tekstów, wyrażeń arytmetycznych lub tekstowych i funkcji. W formule logicznej muszą wystąpić dwa z wymienionych elementów połączone jednym z operatorów relacji. Operatory te znane są każdemu z lekcji matematyki. Niektóre z nich zapisywane są w regule jako dwa kolejne znaki. Oto te operatory:

• Operator równości „=”
• Operator nierówności „<>”, zapisywany dwoma znakami, na klawiaturze brak symbolu „≠”
• Operator większości „>”
• Operator niemniejszości „>=”, zapisywany dwoma znakami, na klawiaturze brak symbolu „≥”
• Operator mniejszości „<”
• Operator niewiększości „<=”, zapisywany dwoma znakami, na klawiaturze brak symbolu „≤”

Aby ułatwić sobie zrozumienie formuł i ich istotę, możemy odczytywać je zaczynając zdaniem „czy prawdą jest, że…” i dalej już sama formuła. Oto przykład takiej formuły: „=5>7” i jej odczyt, „czy prawdą jest, że pięć jest większe od siedem?” Oczywiście jest to nieprawdą, więc wartością wyświetloną w komórce z taką formułą będzie FALSE. Arkusz porównał tutaj ze sobą dwie liczby.

Inna formuła mogłaby wyglądać np. tak „="Krzysztof"<"Jan"”. Tutaj porównanie dotyczy dwóch tekstów i określenia, który z nich jest większy. Przy porównywaniu tekstów, porównuje się pary znaków w obu tekstach na kolejnych pozycjach, od lewej do prawej. „Większym” jest ten tekst, który na tej samej pozycji ma „większą” literę. W tekstach „najmniejszym” znakiem jest spacja, potem są znaki w rodzaju kropka, przecinek, następnie cyfry a w końcu litery, najpierw mała a potem wielka. Sześć kolejnych znaków „A7a:bB” ułożone wg wzrastającej ich wartości, to „:7aAbB”. W utworzonej formule już na pierwszej pozycji obu tekstów występują różne litery „K” i „J”. Ponieważ litera „J” jest wcześniej w alfabecie niż litera „K”, to jest „mniejsza”, a zatem wyrażenie ma wartość FALSE.

Wykorzystując poznane już formuły arytmetyczne, możnaby zapisać np. taką formułę: „=(B3+C3)*3<=18”. Tutaj, arkusz najpierw wyliczy wartość wyrażenia arytmetycznego, uwzględniając nawiasy i wartości znajdujące się aktualnie w komórkach „B3” i „C3” i dopiero potem porówna ten wynik z liczbą 18. Wynikiem tej formuły będzie TRUE lub FALSE, zależnie od wartości znajdujących się we wspomnianych komórkach.

Istnieje pewna właściwość związana z formułami i wyrażeniami logicznymi. Otóż ich wartości, czyli TRUE i FALSE mają reprezentację arytmetyczną taką, że wartości FALSE odpowiada liczba 0 (zero) a wartości TRUE liczba 1.

Budowanie formuł.

Budowanie formuł możliwe jest na dwa sposoby, albo nawet na trzy, jeśli ten trzeci jest sposobem mieszanym, wynikającym ze sposobu pierwszego i drugiego. Pierwszy sposób, to wpisanie po prostu całej formuły w sposób dokładnie odzwierciedlający nasze intencje. Gdy więc w komórce np. C1 należy wprowadzić formułę „=A1+B1”, należy uaktywnić komórkę C1 a następnie wpisać do niej kolejno znaki „=”, „A”,”1”, „+”, „B”, „1” i nacisnąć klawisz ENTER. Formuła zostanie zatwierdzona, a w komórce wyświetlona wartość wynikająca z aktualnej zawartości komórek A1 i B1.

Drugi sposób wykorzystuje możliwość wskazywania komórek biorących udział w formule. Tak więc w przypadku powyższego przykładu, po ustawieniu aktywnej komórki na C1, i po wpisaniu znaku „=” można po prostu kliknąć komórkę A1, albo przy pomocy klawiszy ze strzałkami naprowadzić komórkę aktywną na komórkę A1. Spowoduje to pojawienie się tego adresu bezpośrednio po znaku równości. Teraz można wpisać znak „+” i ponownie wskazać następny potrzebny adres, w tym wypadku B1. Naciśnięcie klawisza ENTER kończy wprowadzanie formuły, jak poprzednio.

Ten drugi sposób tworzenia formuł jest „obsługiwany” we wszystkich arkuszach kalkulacyjnych i znacznie ułatwia i upraszcza tworzenie formuł.

Poniżej, w krótkiej prezentacji przedstawiam zachowanie się programów arkuszowych Google Docs, Excel 2007 i Calc przy wprowadzaniu danych do komórek. W drugiej części tej prezentacji zacznie powstawać zestawienie, w którym zademonstruję zasady formatowania liczb oraz nadawania takim zestawieniom walorów estetycznych. Przedstawiona zostanie także jedna i druga metoda budowania formuł.

Prezentacja po konwersji. Naprowadź myszkę na ten tekst aby przeczytać uwagę.

Następna część opracowania poświęcona jest funkcjom w arkuszach kalkulacyjnych.

Powrót do części poprzedniej.