Yestok.pl

Kiedy poznaliśmy podstawy dokonywania wpisów i budowania formuł. Kiedy wiemy jaka jest rola funkcji, można zacząć budować aplikację spełniające oczekiwane obliczenia. Zazwyczaj na samym początku tej pracy wiemy co chcemy osiągnąć ale nie do końca sprecyzowany pomysł jak to zrobić. W miarę budowy projektu mogą pojawiać się nowe rozwiązania, nowe koncepcje i nieraz całkowicie odmienna – jak to się mówi – „filozofia” projektu. Arkusz kalkulacyjny jest niezwykle wobec nas przyjazny, i jest w stanie ścierpieć wszelkie przeróbki.

Budowanie formuł w arkuszu może być ciekawym wyzwaniem dla naszego umysłu. Musimy bowiem umiejętnie sformalizować zależności występujące między zgromadzonymi danymi. Częstokroć tak samo sformułowana zależność musi wystąpić w wielu kolejnych komórkach. Jeszcze raz przytoczę ilustrację z poprzedniej części opracowania.

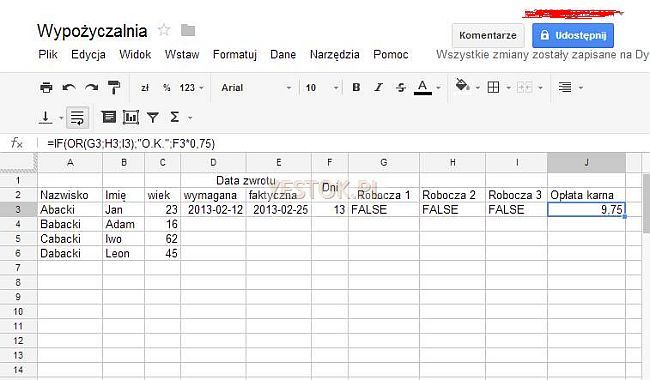
Przyglądając się tej naszej hipotetycznej wypożyczalni, łatwo zauważyć, że formuły wpisane do komórek G3, H3, I3 czy J3 powinny w swej istocie pojawić się w komórkach następnych wierszy, zmieniając odpowiednio adresy komórek w tych formułach występujących. I musi to wystąpić w tylu wierszach, ile wykorzystuje to zestawienie. Wpisywanie tych formuł w kolejne komórki, zwłaszcza gdyby lista naszych użytkowników była znaczna, raczej zniechęciłoby nas do korzystania z arkusza kalkulacyjnego niż przekonało do jego użyteczności.

Poznajmy najpierw czym są adresy komórek wpisywane do formuł.

Względność i bezwzględność adresów.

Adresy wpisywane do tworzonych formuł są w nich interpretowane w specyficzny sposób. Z jednej strony rzeczywiście wskazują formule skąd ma zostać pobrana wartość, z drugiej, i tego już nie „widzimy”, mówią „zlokalizuj to miejsce względem mojego obecnego położenia”. Wyjaśnię to opisowo. Poniżej przedstawione zostało zestawienie, w którym dla każdego pojazdu w firmie podano przebieg i ilość zużytego paliwa.

Obliczyć należy wartość spalania na 100 km. Zamieszczona w komórce E6 formuła ma postać „=C6/B6*100” wyliczając widoczną wartość 7,00. Formuła rzeczywiście pobiera potrzebne dane z komórek C6 i B6, ale jednocześnie „wie” że ma interpretować adres C6 jako komórkę leżącą w tym samym wierszu, lecz o dwie kolumny na lewo. Komórkę B6 ma interpretować jako leżącą o trzy kolumny na lewo, względem siebie samej. Wpisanie adresu komórki do formuły oznacza zatem podanie usytuowanie tejże względem komórki z formułą. Ta zasada tworzenia formuły pozwala na wykorzystanie mechanizmu kopiowania komórek z formułą, do innych komórek. W docelowych miejscach, skopiowane formuły nie zawierają adresów znajdujących się w źródle, lecz odpowiadające adresy położone w takim samym porządku względem skopiowanej formuły jak w komórce źródłowej. To oznacza, że jeśli skopiujemy zawartość komórki E6 do komórek E7, E8 i E9 to skopiowane tam formuły będą odwoływały się do adresów w taki sam sposób jak to ma miejsce w komórce E6. A to oznacza, że w ten sposób możemy powielić wymaganą formułę do wielu komórek. Tak wpisywane do formuły adresy nazywamy adresami względnymi.

Istnieją oczywiście sytuację, kiedy względność adresów nie jest pożądana. Zobaczymy to w tym samym przykładzie, obliczając koszt zużytego paliwa. W komórce B3 tego zestawienia umieściłem cenę jednego litra benzyny. Formuła obliczająca koszt paliwa dla pierwszego pojazdu, wpisana do komórki D6 miałaby postać „=C6*B3”. Taki zapis dla formuły oznaczałby, że do jej wyliczenia należy pobrać zawartość komórki leżącej w tym samym wierszu, dwie kolumny w lewo oraz komórki leżącej o trzy wiersze wyżej i trzy kolumny w lewo. Wynik obliczenia zostanie wyświetlony w komórce. Gdyby jednak skopiowano tę formułę, tak jak poprzednią, do odpowiadających komórek D7, D8 i D9 to obliczenia w nich nie byłyby prawidłowe. We wszystkich formułach poprawnie pobierana byłaby ilość paliwa, bo dla każdej z nich znajduje się ona o dwie kolumny w lewo w tym samym wierszu. Cena benzyny byłaby jednak pobierana dla każdej formuły z innego miejsca tabelki, bo każda formuła sięgałaby do komórki leżącej trzy wiersze wyżej i trzy kolumny w lewo. W przypadku takiej formuły chcemy aby „zużycie w litrach” było adresem względnym, ale „cena paliwa” – adresem bezwzględnym. I tak brzmi określenie tego typu adresu. Adres bezwzględny to taki, który zawsze pokazuje na tę samą komórkę, bez względu na to, gdzie zostanie skopiowany. Adresy tego typu zapisywane są z dodatkowymi symbolami „$”. Zatem aby móc spokojnie przekopiowywać formułę, powinna ona zostać zapisana jako „=C6*$B$3”. Taki zapis oznacza, że we wszystkich skopiowanych miejscach adres C6 zostanie zastąpiony odpowiednim adresem względnym, natomiast adres komórki B3, jako bezwzględny, nie zostanie zmieniony i w takiej postaci wystąpi w każdej kopii formuły.

Aby ułatwić wprowadzanie adresu bezwzględnego, we wszystkich arkuszach można wprowadzić adres w zwykły sposób a następnie, gdy wskaźnik kursora tekstowego mruga na adresie, nacisnąć klawisz F4 na klawiaturze (w programie Calc wersji Apache OpenOffice musi to być SHIFT+F4). Naciskanie klawisza powoduje zmianę postaci adresu w pewnej sekwencji. Dla przykładowego adresu A1 będzie to: A1⇒$A$1⇒A$1⇒$A1 a następnie ponownie A1, itd. Trzecia postać adresu oznacza adres o kolumnie względnej lecz wierszu bezwzględnym a czwarta, adres o kolumnie bezwzględnej lecz wierszu względnym. Takie zapisy są także wykorzystywane, choć na początkowych etapach tworzenia zestawień nie zawsze łatwe i oczywiste do zastosowania.

Można oczywiście wpisywać samodzielnie wszystkie znaki adresu bezwzględnego. Korzystanie z działania klawisza F4 możliwe jest także podczas poprawiania istniejących formuł. Jeśli mrugający kursor tekstowy będzie znajdował się w obrębie sygnatury adresu, naciskanie klawisza F4 będzie zmieniało adres, zgodnie z pokazanym powyżej cyklem.

Kopiowanie komórek.

Scenariusze kopiowania w arkuszach są trzy. Kopiować można jedną komórkę w inne miejsce, można skopiować jedną komórkę do wielu miejsc, można też skopiować zaznaczony wcześniej obszar w inne miejsce. Pod względem procedury, kopiowanie jest takim samym kopiowaniem jak w edytorze tekstowym. Zaznaczamy komórkę źródłową lub obszar źródłowy, i wybieramy opcję „Kopiuj”, najprościej wydaje się jest skorzystać ze skrótu klawiaturowego „CTRL+c”, który we wszystkich systemach znaczy to samo, czyli „skopiuj do schowka”. Można też kliknąć prawym przyciskiem myszki na wybranym źródle i wybrać polecenie „Kopiuj”, które pojawi się w menu kontekstowym, albo wybrać polecenie kopiuj z menu „Edycja”, dostępnego w pasku poleceń. Następnie należy wskazać komórkę docelową, lub zaznaczyć docelowy obszar, jeśli kopiujemy komórkę do wielu komórek. Wklejenie zrealizuje zarówno skrót klawiaturowy „CTRL+v” oznaczający „wklej ze schowka”, jak i wywołanie polecenia „Wklej” z rozwiniętego polecenia „Edycja” czy rozwiniętego menu kontekstowego (po kliknięciu prawym przyciskiem myszki). Gdy kopiujemy wiele komórek na raz, należy je najpierw zaznaczyć i dopiero potem użyć kopiowania, następnie wystarczy wskazać komórkę, w której ma znajdować się lewy, górny róg kopiowanego obszaru i wybrać wklejanie.

We wszystkich arkuszach zaimplementowano pewien specjalny sposób kopiowania. Prawy dolny róg komórki aktywnej jest wyróżniony. Widać to na wszystkich ilustracjach. Naprowadzenie wskaźnika myszki na ten punkt, zmieni wygląd tego wskaźnika. Kliknięcie i przeciągnięcie tego zmienionego wskaźnika w obszarze arkusza, spowoduje skopiowanie komórki do całego wyznaczonego w ten sposób obszaru. Ten sposób pozwala na skopiowanie zawartości komórki do komórek przyległych.

Jeżeli kopiowana komórka lub kopiowany obszar będą zawierały zwykłe wpisy, to zostaną one po prostu skopiowane w nowe miejsce. Jeśli jednak będą zawierały formuły to zostaną skopiowane te formuły z zachowaniem zasad adresowania względnego. Niezmienione zostaną tylko adresy bezwzględne.

Scalanie komórek.

Czasami struktura tabeli wymaga aby niektóre komórki zajmowały więcej miejsca niż inne w tej samej tabeli. Widać to np. na pierwszej ilustracji, na której tytuł "Data zwrotu" rozciąga się przez dwie kolejne szerokości kolumn. Dowolnie wiele przyległych do siebie i tworzących prostokąt komórek można połączyć w jedną dużą komórkę. Nazywa się to scalaniem i ikona realizująca tę operację była pokazana w poprzedniej części opracowania. Efekt ten najczęściej wykorzystuje się do tworzenia nagłówków złożonych tabel, jednak taka komórka traktowana jest jak każda inna i może zawierać dowolny rodzaj wpisu o jakim była mowa w tym opracowaniu, każdy rodzaj formatowania czy wyrównania.

Ikonka narzędziowa scalania uaktywnia się tylko wówczas gdy zaznaczony jest obszar przynajmniej dwóch przyległych komórek. Ikonka ta jest także aktywna, gdy uaktywniona jest komórka wcześniej scalona, ale jej działaniem jest wówczas podział scalonej komórki na jej pierwotne obiekty.

Reorganizacja arkusza.

Czasami na skutek nowych pomysłów uznamy, że komórka zawierająca formułę powinna znajdować się w innym miejscu. Arkusze pozwalają na przeniesienie zawartości komórki w nowe miejsce i nie „psują” zbudowanej formuły. Jeśli zatem w komórce wpisana jest formuła odwołująca się do jakichś adresów, to przeniesiona formuła nie ulegnie zmianie. Będzie nadal odwoływała się do adresów do niej wpisanych, chociaż zmienią się wewnętrzne odwołania względne do tych komórek. Jeśli natomiast zostanie przeniesiona komórka zawierające dane wymagane w innych formułach, to we wszystkich takich formułach jej stary adres zostanie zastąpiony nowym. Taki sposób działania oznacza zatem, że można w każdej chwili dodać nowe kolumny czy wiersze a dotychczas zdefiniowane formuły nadal będą prawidłowo obliczały wyniki.

Aby przenieść komórkę, lub obszar komórek w inne miejsce należy zaznaczyć odpowiednie elementy, tak jak przy kopiowaniu, a następnie wybrać działanie „Wytnij” z menu „Edycja”, „Wytnij” z menu kontekstowego dostępnego po kliknięciu prawym przyciskiem myszki lub nacisnąć skrót klawiaturowy CTRL+x. Skrót ten we wszystkich aplikacjach oznacza wytnij i zachowaj w schowku. Teraz należy wskazać miejsce docelowe i wybrać polecenie „Wklej”, w dowolny sposób, omówiony już przy kopiowaniu. Na tę operację arkusze kalkulacyjne reagują różnie. Arkusz Google i Excel realizują zadanie wycinania nie zmieniając jednak wyglądu wycinanego obszaru, to znaczy nie opróżniają go przed wykonaniem operacji „Wklej”, i czekają na wskazanie gdzie wycięte komórki mają zostać wstawione. Operacją „Wytnij” nie można więc w tych programach usunąć danych, gdyż zaniechanie dalszego działania nie zmienia zawartości arkusza. Calc, faktycznie wycina komórki, a więc usuwa ich zawartość, co może powodować zmiany w wynikach wpisanych formuł. Formuły te odwołują się bowiem w tym momencie do komórek których już nie ma. Wracają one jednak, te wyniki, do właściwych wartości po wklejeniu wyciętych obszarów.

Arkusze pozwalają także na przeniesienie komórki lub obszarów przez przeciągnięcie ich w nowe miejsce. Wskaźnik myszki zmienia swój kształt na granicy aktywnej komórki lub zaznaczonego obszaru, co sygnalizuje możliwość przeciągnięcia tegoż w nowe miejsce. W arkuszu Google jest to kształt rączki, w Excelu poczwórna strzałka. Jedynie Calc nie sygnalizuje tej gotowości. Przeciągnięcie komórek w nowe miejsce jest równoważne wycięciu ich w starym miejscu i wklejeniu w nowym.

Arkusze rozpoznają sytuacje, w których zechcemy wkleić dane do komórek, które zawierają już inne dane i zazwyczaj informują o tym specjalnym komunikatem, żądając decyzji czy takie zdarzenie ma nastąpić.

Kolumny i wiersze.

Zarządzanie kolumnami i wierszami sprowadza się w ogólności do dodania nowego elementu, usunięcia niepotrzebnego, zmiany niektórych ogólnych parametrów wiersza lub kolumny, w końcu możliwości ukrycia go w strukturze arkusza. Na rysunku poniżej przedstawiony jest pewien stan ekranu arkusza.

Kiedy naprowadzi się wskaźnik myszki w pobliże litery określającej nazwę kolumny, po jej prawej stronie pojawi się charakterystyczny przycisk, na ilustracji oznaczony cyfrą „1”. Kliknięcie tego przycisku otwiera listę możliwych działań dostępnych dla tej kolumny. Taką rozwiniętą listę dla kolumny „C” pokazuje ramka oznaczona cyfrą „2”.

Działania reorganizujące tabelę a więc i arkusz, to wstawienie jednej kolumny z lewej albo z prawej strony wybranej kolumny. Wstawienie kolumny z lewej strony w tym konkretnym przykładzie oznacza, że wstawiona kolumna oznaczona zostanie literą „C”, zatem dotychczasowa kolumna „C” zostanie przemianowana na „D” i dalsze odpowiednio. Wszystkie znajdujące się w arkuszu formuły zostaną zmodyfikowane, i nadal będą prawidłowo wyliczały wartości.

Usunięcie kolumny oznacza, że kolumna znika i jej literowe oznaczenie przejmuje kolumna sąsiednia. Ta operacja może spowodować zmiany w obliczeniach, gdyż usuwana kolumna może zawierać np. formuły obliczeniowe albo dane niezbędne w innych obliczeniach. Arkusze zachowują się różnie w tej sytuacji. Usunięcie formuł zmienia po prostu układ tabeli i nie wpływa na arkusz. Usunięcie komórek, które biorą udział w obliczeniach w innych częściach arkusza, powoduje jednak inne działanie. Arkusz Google zastąpi w tych formułach dotychczasowy adres symbolem {} i spróbuje zrealizować obliczenia jeśli to jest możliwe. Excel i Calc traktują takie formuły jako uszkodzone i w miejsce wszystkich usuniętych adresów w formułach wpisują „ADR!”. Wynikiem takich formuł będzie wyświetlona wartość #ADR!. Wszystkie formuły, które korzystają nawet pośrednio z komórek, których wynikiem jest wartość #ADR! będą także miały wynik #ADR!.

Wyczyść kolumnę oznacza żądanie opróżnienie wszystkich komórek w kolumnie. Będą one teraz komórkami pustymi. Może to oczywiście mieć wpływ na zaprogramowane w tabeli obliczenia ale nie wpłynie na formuły.

Ukryj kolumnę oznacza, że kolumna ma być niewidoczna w arkuszu, chociaż zawiera różne dane lub formuły. Ukrycie kolumny „C” spowodowałoby, że w arkuszu, w nagłówkach kolumn, widoczne byłyby litery „A”, „B”, „D” itd. Na granicy kolumn „B” i „D”, przy literowych symbolach tych kolumn, pojawią się charakterystyczne znaczniki, informujące że między nimi znajduje się jedna lub więcej ukrytych kolumn. Kliknięcie myszką w taki znacznik przywróci wyświetlanie tych ukrytych kolumn. Ta funkcja pozwala wykorzystywać pomocnicze komórki do własnych obliczeń, ukrywając je jednak przed użytkownikiem końcowym. Komórki takie nie pojawiają się oczywiście na drukowanych zestawieniach.

Analogiczne polecenia pojawią się po kliknięciu prawym przyciskiem myszki w numer wiersza znajdujący się na lewej krawędzi okna arkusza.

Jeżeli zaznaczonych zostało więcej kolumn lub wierszy, to wspomniane operacje odniosą się do liczby zaznaczonych obiektów. Jeśli zaznaczonych zostało np. pięć wierszy lub kolumn, to polecenie usuń, usunie tych pięć wierszy lub kolumn, polecenie wstaw wstawi pięć wierszy lub kolumn, a ukryj – ukryje pięć wierszy lub kolumn.

Zmień rozmiar kolumny – ta opcja pozwala dopasować szerokość kolumny do wymaganej wielkości. Otwarte nowe okienko, uszczegóławiające to działanie, pozwala określić szerokość kolumny. Szerokość ta ustalana jest w tak zwanych pikselach, czyli liczbie punktów ekranowych wyświetlających obraz albo przez wybranie opcji „Dopasuj do danych” powodującej, że szerokość kolumny zostanie dopasowana do najszerszego wpisu znajdującego się w kolumnie. W przypadku wielowierszowych zestawień, pozwala to na dobranie szerokości bez śledzenia wszystkich wpisów. Szerokość kolumny w arkuszu można także zmienić poprzez przeciągnięcie myszką w lewo lub w prawo pionowej linii dzielącej literowe oznaczenia kolumn (linia ta wyraźnie się pogrubia). W przypadku wiersza, poprzez przeciągnięcie w górę lub w dół poziomej linii dzielącej numery wierszy (tu także zmieni się kształt linii). Ale zrobić to można tylko w obszarze tych literowych oznaczeń (jeśli chodzi o kolumny) lub liczbowych oznaczeń wierszy, gdy chodzi o wiersze. Zmieniony wskaźnik myszki jednoznacznie zasygnalizuje możliwy kierunek przeciągania.

Nie są to wszystkie polecenia dostępne w tym rozwiniętym menu. Ponieważ opracowanie kierowane jest do początkujących użytkowników, na razie inne zostaną pominięte.

Zarządzanie arkuszem.

Ogólne zarządzanie arkuszem zrealizować można wykorzystując pasek poleceń i wyświetlone w nim grupy poleceń. Użytkownik znajdzie tu grupy: Plik, Edycja, Widok, Wstaw, Formatuj, Dane, Narzędzia i Pomoc.

Każda grupa zawiera dalszą rozwijaną listę poleceń i opcji, przy pomocy których można wykonać wiele działań. Niektóre z nich już poznaliśmy opisując pasek narzędziowy. Na przykład wszystkie polecenia formatowania komórek znajdują się w grupie poleceń „Formatuj”. W grupie „Edycja” znajdziemy polecenia m.in. „Wytnij”, „Kopiuj” i „Wklej”, ale także usuń wiersz lub kolumnę a w grupie „Wstaw” polecenia pozwalające wstawić do arkusza wiersz, kolumnę, funkcję czy rysunek.

Z ważniejszych możliwości o jakich chcę jeszcze tu wspomnieć, to znajdujące się w grupie „Widok” polecenia „Zablokuj wiersze” i „Zablokuj kolumny”. Polecenia te przydadzą się gdy zbudowana tabela będzie bardzo duża, np. zawierająca 25 kolumn i 400 wierszy, lub więcej. Podczas przewijania takiej tabeli w oknie arkusza, znikają nagłówki tabeli, zajmujące zazwyczaj jeden lub kilka pierwszych wierszy zestawienia, znika też boczek zestawienia, jeśli był zdefiniowany. W efekcie użytkownik widzi mnóstwo zestawionych danych, ale nie bardzo może dopasować je do konkretnych cech i opisów. Zablokowanie wierszy spowoduje, że podczas przeglądania dalszej części zestawienia, wiersze wskazane jako zablokowane będą stale widoczne. To samo dotyczy zablokowania kolumn. Dzięki temu na ekranie zawsze widoczny będzie odpowiedni nagłówek i boczek zestawienia. Aplikacja pozwala zablokować od jednego do dziesięciu wierszy i od jednej do pięciu kolumn.

W tej grupie poleceń można także włączyć lub wyłączyć wyświetlanie siatki pokazującej granice komórek. Ukryć lub przywrócić wyświetlanie paska wprowadzania. Oraz wykorzystując opcję „Wszystkie formuły” spowodować wyświetlanie w komórkach wpisanych do nich formuł a nie wyników tych formuł. Taki sposób oglądu zestawienia może być przydatny, gdyż szybko możemy sprawdzić gdzie znajdują się formuły obliczeniowe, zazwyczaj jednak szerokość kolumn nie pozwoli na wyświetlenie całej wpisanej formuły i jeśli chcemy ją zobaczyć w całości trzeba kolumnę poszerzyć.

Arkusz Google, podczas pracy użytkownika, zapamiętuje na bieżąco wszystkie zmiany w specjalnym obszarze, na wirtualnym dysku Google związanym z kontem użytkownika. Dlatego w grupie poleceń „Plik” nie ma polecenia „Zapisz”. Dokumenty w dysku Google zapisywane są na bieżąco pod nazwą ustaloną przez użytkownika. Nowy, pusty skoroszyt ma nazwę „Arkusz kalkulacyjny bez tytułu”, jak na poniższej ilustracji.

Kliknięcie myszką w obszar tego napisu otworzy nowe okno dialogowe, w którym można zdefiniować własną nazwę dla projektu. Pod tak określoną nazwą projekt będzie zapisany na dysku Google. Widoczna obok napisu zagięta strzałka, jest przyciskiem przenoszącym użytkownika do dysku Google, pozwalając w ten sposób wybrać dowolny inny, wcześniej zapisany, projekt do edycji.

Polecenie „Plik” w opcji „Nowy” pozwala utworzyć nowy projekt. Usługa Google Docs obejmuje oprócz arkusza kalkulacyjnego, także: dokumenty, prezentacje, formularze i rysunki, więc można wybrać dowolny z nich.

Jeśli użytkownik chce wykorzystać swój projekt w komputerze stacjonarnym, z wykorzystaniem innego arkusza kalkulacyjnego, Excel albo Calc, może wysłać go jako załącznik pod zadany adres mailowy (np. własny), wybierając wcześniej format tego załącznika. Możliwość tę oferuje jedno z poleceń opcji „Plik”.

Inne polecenie w tej grupie – „Otwórz” – pozwoli wybrać do edycji dowolny z projektów zapisanych w dysku Google, ale też pozwoli na przesłanie na ten dysk pliku arkusza Excel lub Calc z własnego komputera, a następnie otworzenia go do edycji.

W grupie poleceń „Plik” znajduje się także polecenie „Drukuj”, umożliwiające wydrukowanie zestawienia. W tym przypadku, w otwartym oknie dokładniejszego sprecyzowania opcji wydruku, można dopasować wydruki do własnych wymagań. Pierwszym oknem dialogowym tego polecenia będzie zaprezentowane poniżej.

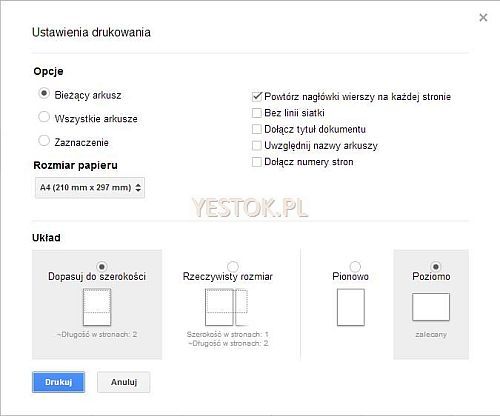
W tym oknie użytkownik wybiera co zostanie wydrukowane, bieżący arkusz, wszystkie arkusze czy zaznaczony w arkuszu obszar.

Rozwijana lista rozmiarów papieru, pozwala wybrać jego format.

Pięć opcji po prawej stronie decyduje o wyglądzie wydruku. Pierwsza, „Powtórz nagłówki wiersza na każdej stronie” oznacza, że jeśli zablokowano w arkuszu jakieś wiersze lub/i kolumny, i tylko wtedy (była o tym mowa przed chwilą), to te zablokowane wiersze i kolumny pojawią się na każdej kartce wydruku.

Druga opcja oznacza, że na wydruku nie będzie linii siatki.

Opcja trzecia „Dołącz tytuł dokumentu” spowoduje, że w nagłówku każdej strony zostanie wydrukowana nazwa dokumentu. Jeśli włączono także opcję czwartą, „Uwzględnij nazwy arkuszy”, to po nazwie dokumentu zostanie także wydrukowana nazwa drukowanego arkusza.

Ostatnia opcja, „Dołącz numery stron” spowoduje drukowanie w stopce strony, na środku, numeru drukowanej strony.

Ostatnie parametry tego okna pozwalają wybrać układ papieru oraz decydują o tym czy wydruki mają zostać dopasowane do szerokości papieru.

Ustalenie tych parametrów i wybór przycisku „Drukuj” otworzy kolejne okienko. Okienko to przedstawia rys. 6. Przedstawia ono kolejne opcje, przy czym widoczny po prawej stronie podgląd wydruku, dotyczy sytuacji, kiedy w pierwszym oknie, tym przedstawionym na rys. 5, włączono wszystkie pięć opcji.

Aby zaprezentować funkcjonalność tej opcji, dodałem do arkusza podlegającego drukowaniu kilkanaście pustych wierszy, tak aby – w sztuczny co prawda sposób – powstał arkusz dwustronicowy. Ponadto w arkuszu tym zablokowałem trzy wiersze.

Prawa strona tego okna przedstawia efekt końcowy jaki pojawi się na drukarce. Widać, że wydruk będzie składał się z dwóch stron, na których każdorazowo powtórzone zostaną trzy pierwsze wiersze. Ilustracja tego nie odzwierciedla wyraźnie, ale w górnej części stron, w nagłówku, pojawi się tytuł dokumentu, w tym wypadku będzie to tekst „Arkusz kalkulacyjny bez tytułu” a po myślniku pojawi się napis „Arkusz1”. U dołu strony, w stopce zostanie umieszczony kolejny numer strony. Na wydruku nie będzie linii siatki.

Po lewej stronie okienka, użytkownik może wybrać drukarkę, na której ma powstać wydruk. Może też zdecydować, które strony dokumentu mają zostać wydrukowane, w ilu kopiach i czy w kolorze, czy nie.

Na tym zakończę opracowanie, które nazwałem „Arkusz kalkulacyjny dla absolutnie zielonych”. Zdaję sobie sprawę, że nie poruszyłem w nim wielu problemów, ot choćby generowania wykresów, traktowania arkusza jako prostej bazy danych, ochrony arkusza i komórek przed zmianami czy stosowania własnych nazw do komórek i obszarów. A to i tak tylko część nieporuszonych tematów. Wyszedłem jednak z założenia, że skoro to co tu napisałem przeznaczone jest dla „absolutnie zielonych” to powinienem omówić zagadnienia, które pozwolą takiej osobie zbudować swoje własne, pierwsze zestawienie i osiągnąć z tego tytułu satysfakcję. Zrozumienie podstaw, łatwiej prowadzi do zrozumienia i stosowania rozwiązań bardziej zaawansowanych.

Przykład arkusza kalkulacyjnego.

Na zakończenie w poniższej prezentacji przedstawiam utworzenie prostego zestawienia z wykorzystaniem tego o czym mowa jest w opracowaniu.

Przykład jaki chciałbym zademonstrować w pokazie, ma w miarę możliwości odpowiadać rzeczywistej sytuacji. Prawdopodobnie nigdy tak nie będzie, gdyż każda sytuacja jest inna i indywidualna, spróbuję jednak zbliżyć się do realiów.

Chcę rozwiązać problem obliczenia kosztów malowania mieszkania. Mamy np. małą firmę rodzinną i chcemy łatwo i szybko oszacowywać koszty robót u klienta. Postaram się rozwiązać ten problem za pomocą arkusza kalkulacyjnego. Wykorzystam trzy arkusze. Arkusz przy pomocy którego dokonam obmiaru prac, arkusz skalkulowania prac i arkusz cennika farb.

Zakładam, że wszystkie pomieszczenia mają ściany postawione zawsze pod kątem prostym. Dla typowego prostokątnego pomieszczenia nie ma problemu obmiaru gdyż w zasadzie dwa wymiary wystarczą na dokonanie obliczeń. Ponieważ pomieszczenia, które malujemy mogą mieć różne kształty, to proponuję sposób obmiaru, który wyjaśnię na przykładowym schemacie. Rysunek poniżej przedstawia taki przykładowy schemat pomieszczenia. W rozważanym przykładzie pomijam problem okien i drzwi.

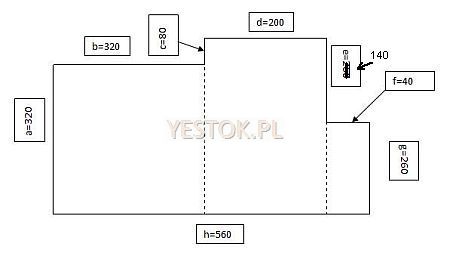
Literami oznaczone są wszystkie ściany pomieszczenia. Jego powierzchnię wyznaczają trzy prostokątne obszary. Pierwszy a × b, drugi (a+c) × d i trzeci f x g. Natomiast powierzchnię ścian wyznacza iloczyn (a+b+c+d+e+f+g+h) × wysokość pomieszczenia.

Pomieszczenia mogą być nawet bardziej „połamane”, dlatego w budowanym arkuszu przewidziałem więcej ścian. Wykorzystamy natomiast tylko tyle, ile będzie potrzebnych.

Arkusz ma działać tak:

Po wprowadzeniu danych obmiarowych powinna zostać obliczona powierzchnia ścian do pomalowania i powierzchnia sufitu.

Arkusz zawierający cennik zorganizowany jest wg poniższej tabelki:

Arkusz kalkulacji wymaga podania dodatkowo informacji, jaka farba ma zostać użyta i czy będzie to farba kolorowa? Ile razy pomieszczenie ma zostać pomalowane, czyli ile warstw farby ma zostać położone? Zakładam też, że sufit będzie zawsze biały.

Na podstawie wprowadzonych danych i informacji z cennika, arkusz powinien wyliczyć ile litrów farby będzie potrzebne i ile będzie kosztowała.

Załączona prezentacja wykorzystuje dane podane w zaprezentowanym powyżej schemacie pomieszczenia.

Proszę pamiętać, że jest to tylko przykład, którego zadaniem jest pokazanie możliwości arkusza. Konkretne zastosowanie do celów jakie tu zasugerowałem wymagałoby więcej pracy i przede wszystkim znajomości problemu.

Prezentacja po konwersji. Naprowadź myszkę na ten tekst aby przeczytać uwagę.

W przedstawionej prezentacji nie pokazałem co się stanie, gdy wpisana zostanie nazwa farby, której nie ma na liście w cenniku. Użyta funkcja VLOOKUP z czwartym parametrem o wartości FALSE wymaga, aby poszukiwana wartość wystąpiła w pierwszej kolumnie obszaru przeszukiwania. Jeśli taka wartość nie zostanie znaleziona, funkcja zwraca wartość #N/A. Wszystkie formuły, które skorzystają z wyniku funkcji VLOOKUP także będą miały wartość #N/A. Przedstawia to poniższa ilustracja.

Nazwa farby została wpisana jako Dulex, zamiast Dulux, zatem wszystkie formuły, które bezpośrednio lub pośrednio odwołują się do wyników funkcji VLOOKUP także zwracają wartość #N/A. Naprowadzenie myszki na prawy górny narożnik komórki z wartością #N/A, wyświetli dodatkowy komunikat, wyjaśniający powód takiej wartości. Jeśli natomiast komórka z nazwą farby będzie pusta, to wszystkie formuły zwrócą wartość w postaci dwóch poziomych kreseczek. Te kreseczki to w rzeczywistości wartość #N/A, tylko przedstawiona w ten sposób.

W Excelu i Calcu odpowiednikami #N/A jest #N/D, i wartość taka pojawia się w tych arkuszach także wtedy, gdy szukaną wartością jest pusta komórka.

Powrót do części poprzedniej.