Yestok.pl

Jednym z najpowszechniej używanych programów biurowych jest program określany nazwą „Arkusz kalkulacyjny”. Program ten jest już na tyle skomplikowany, w znaczeniu jego użytkowania, że intuicyjne korzystanie z niego, jak np. w przypadku edytorów tekstów, nie zawsze jest możliwe.

Postanowiłem więc napisać to opracowanie wierząc, że istnieje całkiem spora grupa osób, która chciałaby zrozumieć zasady działania tego programu, a w konsekwencji świadomie tę wiedzę wykorzystać. Nie będzie to oczywiście kurs użytkowania, ale proste wprowadzenie do tematu, pozwalające – jak sądzę – samodzielnie odkrywać dalsze zalety, możliwości i pożytki „wbudowane” w programy tego typu.

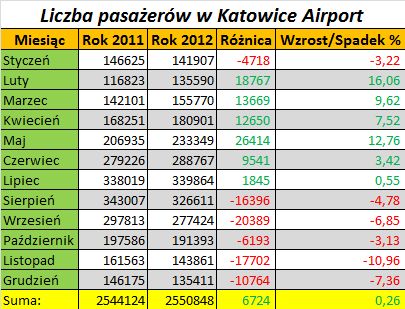
Wszelkiego rodzaju zestawienia tabelaryczne od dawna towarzyszą nam w życiu codziennym. Większość z nich to rzeczywiście zwykła tabelka, jak ta prezentowana poniżej, znajdująca się na opakowaniu produktu spożywczego.

Inna, bardziej skomplikowana, może zawierać szereg danych liczbowych o jakimś obszarze działalności gospodarczej, kulturalnej, społecznej lub np. zdrowotnej. Bardzo często niektóre z liczb znajdujących się w takiej tabeli są wynikami obliczeń na innych wartościach liczbowych z tej samej tabeli.

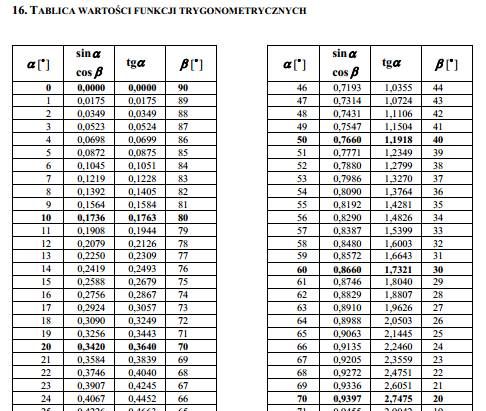
Jeszcze inne zestawienia tabelaryczne to zestawienia matematyczne, inżynierskie i inne tego rodzaju. W czasach szkolnych wszyscy chyba korzystali z tablic matematycznych, zawierających różnego rodzaju przeliczenia i wartości związane z matematyką. Jedną z takich tablic można sobie przypomnieć oglądając poniższy rysunek.

To właśnie konieczność tworzenia zestawień tabelarycznych natchnęła Dana Bricklina, studenta Harvard Business School i zaproszonego po pewnym czasie do współpracy kolegę z Massachusetts Institute of Technology (MIT), Boba Frankstona, do napisania specjalnego programu usprawniającego ten proces. Usprawniającego w całkowicie rewolucyjny sposób, pozwalał on mianowicie na budowanie zależności między danymi wprowadzonymi do tabeli i dowolną reorganizację tych danych bez utraty zdefiniowanych zależności. 17 października 1979 do sprzedaży trafił VisiCalc pierwszy program tego rodzaju, przeznaczony dla najpopularniejszego w tym okresie komputera Apple II. Od tego też czasu, ten rodzaj programu zaczęto nazywać programem arkusza kalkulacyjnego.

Szacuje się, że sprzedano 800 000 kopii programu VisiCalc. Jak przełomowe znaczenie miał on dla prac obliczeniowych niech świadczy to, że tysiące firm kupowało komputer za 3 000 dolarów po to by używać programu za 150 dolarów. Po latach rozwoju i ewolucji programy arkuszowe są nadal powszechnie używane. Najpopularniejszym obecnie używanym programem tego typu jest Excel, program wchodzący w skład pakietu biurowego Microsoft Office. Obok niego istnieje oczywiście wiele konkurujących programów, wśród których wymienię program o nazwie Calc będący częścią innego pakietu biurowego, bezpłatnego LibreOffice i prawie bliźniaczego, także bezpłatnego, Apache OpenOffice. Wymienię także arkusz kalkulacyjny należący do usługi Google Docs , dostępny dla każdego właściwie urządzenia, które dysponuje przeglądarką internetową i dostępem do Internetu. Ten ostatni arkusz działa bowiem bezpośrednio w przeglądarce internetowej. Niezależnie jednak od konkretnego programu zasada ich pracy jest jednakowa. Zatem znajomość jednego, pozwala w zasadzie korzystać z pozostałych programów.

Artykuł ten ma wyjaśnić zasadę pracy takich programów i umożliwić budowanie prostych zestawień. Mimo tego, że jak wspomniałem najpopularniejszym programem tego typu jest Excel, w tym artykule wykorzystam aplikację Google Docs. Po pierwsze i najważniejsze jest ona dostępna dla każdego użytkownika Internetu, nie trzeba więc instalować żadnego odrębnego programu, co może być ważne dla użytkowników tabletów i smartfonów, więc każdy może spróbować swoich sił. Po drugie, z racji funkcjonowania w przeglądarce, program ten nie jest tak bardzo rozbudowany w różnego rodzaju opcje i możliwości, które na etapie poznawania arkusza nie są aż tak potrzebne. Po trzecie, i tak wszystkie działania będą w ten sam sposób realizowane w pozostałych arkuszach innych producentów. Postaram się jednak napisać o różnicach w Excelu i Calcu, jeśli występują.

Wypada tutaj powiedzieć kilka słów o usłudze Google Docs tym, którzy nigdy z niej nie korzystali. Firma Google udostępniła użytkownikom wiele własnych rozwiązań, wśród których jest usługa określona w polskiej wersji nazwą „Dokumenty Google” czyli właśnie Google Docs i powiązana z nią usługa „Dysk Google”, w oryginale Google Drive. Usługi te umożliwiają tworzenie i edycję dokumentów on-line wspólnie z innymi użytkownikami, w tym samym czasie. Pozwalają też udostępniać poprzez Internet wytworzone dokumenty. Zainteresowani tymi tematami powinni zajrzeć na stronę https://support.google.com/drive/?hl=pl. i upewnić się co do funkcjonalności usługi dla ich systemu operacyjnego. To co opisuję w tym opracowaniu dotyczy systemu operacyjnego Windows.

Aby korzystać z tych usług należy mieć założone konto w usługach Google. Obecnie wiele osób korzysta z adresu pocztowego o nazwie w rodzaju nazwa@gmail.com. Gmail jest także jedną z usług Google, więc zalogowanie się do usługi Google Docs jest możliwe przy pomocy nazwy użytkownika i hasła tej poczty.

Aby przywołać obsługę arkusza we własnej przeglądarce, należy zalogować się do konta w Google. W oferowanych przez Google usługach trzeba odnaleźć sekcję „Dom i biuro” a w nim grupę „Dokumenty”. Firma Google jest także autorem przeglądarki Chrome, twierdzi więc, że najlepiej, najszybciej i najwydajniej arkusze kalkulacyjne zadziałają właśnie w tej przeglądarce. Stosowanie jej jednak nie jest obowiązkowe. Tę aplikację będę nazywał "arkusze Google" . Ponadto zastosowałem się do sugestii Google i wszystkie przykłady realizowałem w przeglądarce Chrome. Mówiąc o arkuszu kalkulacyjnym pomijam całą sferę związaną z rozpowszechnianiem projektów i współdziałaniem wielu autorów nad projektem. Ci, którzy z zagadnieniem arkuszy kalkulacyjnych spotkają się po raz pierwszy, i tak będą mieli sporo nowej wiedzy do poznania.

Jesienią 2013 roku firma Google udostępniła zmodyfikowany produkt nazwany „nowa wersja Arkuszy Google”. Wersja ta była sukcesywnie wdrażana w kolejnych krajach. Obecnie w Polsce wszystkie nowe opracowania tworzone w arkuszach kalkulacyjnych Google powstają w oparciu o tę właśnie nową wersję. Arkusze opracowane wcześniej działają w wersji starszej. Firma Google do końca 2015 roku przeprowadzi migrację wszystkich zapisanych na jej dyskach arkuszy do wersji nowej i wtedy będzie to jedyna dostępna wersja. Przygotowując zestaw artykułów o arkuszach kalkulacyjnych opierałem się o starszą wersję. O tym czy używamy arkusza w nowej wersji informuje specjalny znacznik umieszczony bezpośrednio pod arkuszem. Ilustruje to poniższy rysunek.[dodane: listopad 2014]

Ekrany programów arkuszowych są w gruncie rzeczy bardzo do siebie podobne. Największą część zajmuje siatka tabelki, czyli obszar, do którego wpisujemy dane i w którym dane te po różnych przeliczeniach tworzą inne dane. Siatka linii widoczna na ekranie ma charakter informujący o konstrukcji samej tabeli i nie jest zazwyczaj drukowana na dokumentach wynikowych. A to oznacza, że wymagane obramowania i linie podziału, należy zdefiniować podczas odrębnego procesu ustalającego wygląd zestawień. Powyżej tego obszaru znajdują się paski poleceń lub narzędzi, pozwalające zarządzać różnymi aspektami arkusza. Pod obszarem znajduje się pasek stanu, obrazujący bieżącą sytuację programu.

Poniżej przedstawiam widoki ekranów kilku różnych programów arkuszowych, by czytelnik zorientował się w ich wyglądzie.

Współczesne programy arkuszowe pozwalają na korzystanie jednocześnie z kilku arkuszy. Na powyższych ilustracjach są one oznaczone jako Arkusz1, Arkusz2 itd. lub w wersjach angielskojęzycznych Sheet1, Sheet2…w dolnej części ekranu. Wyjątkiem jest tu arkusz Lotus 1-2-3, który kolejne arkusze oznacza literami „A”, „B” itd., sygnalizując to w górnej części odpowiednią zakładką. Zestaw takich arkuszy przyjęto nazywać skoroszytem. Skoroszyt jest zapisywany jako samodzielny plik, o określonej nazwie. Użytkownik tworząc swój projekt musi wykorzystać przynajmniej jeden arkusz. To arkusz zatem, jako obszar i podstawowa jednostka robocza, wymaga omówienia.

Organizacja arkusza.

Na ekranie wyświetlona jest siatka poziomych i pionowych linii dzielących przestrzeń na kolumny i wiersze. Najmniejszym elementem tej przestrzeni jest komórka, czyli element leżący na przecięciu dowolnego wiersza z dowolną kolumną. Każda komórka arkusza ma swój „adres” czyli identyfikator ją określający. Adres składa się z oznaczenia kolumny i wiersza, na przecięciu których komórka się znajduje. Obecnie na oznaczenie kolumny przyjęto stosować oznaczenie literowe, pierwsza kolumna oznaczona jest literą „A”, druga – „B” i tak dalej. Ponieważ w ten sposób można oznaczyć jedynie 26 kolumn, kolumnę 27. oznacza się dwoma literami „AA”, kolejną – „AB” i postępując w ten sposób dalej dochodzi się do kolumny „ZZ”, będącej 702. kolumną arkusza. Obecnie udostępniane arkusze mają jednak więcej kolumn, Excel 2007 i nowsze oraz Calc z pakietu LibreOffice (od wersji 6) mają ich 16 384, Calc z pakietu Apache OpenOffice (wersja 4.1.15) ma ich (tylko) 1 024. Dlatego kolumna 703 ma już oznaczenie trzyliterowe „AAA” i w konsekwencji ostatnia kolumna Excela 2007 i Calca LibreOffice ma oznaczenie „XFD” zaś ostania Calca Apache OpenOffice – „AMJ”. Oba wspomniane arkusze mają po tyle samo wierszy: 1 048 576. Jednak w programie Calc LibreOffice można w ustawieniach włączyć obsługę bardzo dużych arkuszy, uzyskując możliwość wykorzystania 16 777 216 wierszy. Nieco inaczej wygląda to w arkuszu kalkulacyjnym Google Docs. Tu pojedynczy arkusz nie może mieć więcej niż 256 kolumn, zaś liczba wierszy wynikać będzie z ogólnej dopuszczalnej liczby komórek, których w tym programie może być najwyżej 400 000 we wszystkich arkuszach. Zgodnie z opisanym sposobem adresowania, pierwsza komórka, leżąca w górnym lewym rogu, ma adres A1 zaś ostatnia, leżąca w dolnym prawym rogu ma w programie Calc adres AMJ1048576, a w programie Excel XFD1048576. Ostatnia komórka w arkuszu Google-u, z pełną liczbą dopuszczalnych kolumn i jednym tylko arkuszem, miałaby adres IV1562. Adresy komórek zawsze pisane są łącznie, czyli wskazanie kolumny i wiersza nie jest rozdzielane żadnym innym znakiem. W przypadku podawania adresów komórek nie mają także znaczenia wielkości liter podanych w adresie. Zatem zapis „g34” oznacza to samo co „G34”. Programy arkusza zawsze przekształcają podany adres na postać z wielkimi literami. Dzięki temu nie trzeba zastanawiać się czy np. zapis I3 to wielkie „i” i cyfra 3, czy małe „L” i trójka. W dalszej części tego opracowania, w podawanych przykładach, wszystkie adresy będą pisane wielkimi literami.

Czasami pojawia się potrzeba określenia w arkuszu pewnego obszaru. Obszar jest zawsze elementem prostokątnym, a jego określenie wymaga podania adresów dwóch przeciwległych wierzchołków tej przestrzeni. Zazwyczaj adresy tych wierzchołków rozdzielone są znakiem „:” (dwukropka). Tak więc aby opisać jakiś 12-komórkowy obszar w arkuszu należałoby to zrobić np. tak „C7:F9”. Taki opis dotyczy czterech kolumn (C, D, E, F) i trzech wierszy (7, 8,9). Zwracam uwagę, że fragment wiersza lub kolumny jest także obszarem, zatem zapis np. „C7:C12” oznacza sześć kolejnych komórek w kolumnie „C”, a zapis „C7:H7” – sześć kolejnych komórek w wierszu „7”.

Gdy podczas pracy z arkuszem należy wskazać kilka różnych obszarów lub adresów komórek, to wskazując je, rozdziela się poszczególne elementy znakiem „;” (średnika). Przykładowy zapis „C7:C12;F5;H7:K7” oznacza, że bierzemy pod uwagę obszar sześciu komórek w kolumnie „C”, komórkę „F5” i obszar czterech komórek w wierszu siódmym. Taki zapis nazywany jest też listą.

Podany sposób adresowania jednoznacznie określa komórkę lub obszary w pojedynczym arkuszu. Jeśli jest podany w taki właśnie sposób, oznacza adresy w aktualnie używanym arkuszu. Programy arkuszowe mogą jednak operować na kilku arkuszach, jeśli więc musimy wskazać adres komórki leżącej (lub obszaru leżącego) w innym arkuszu, należy go poprzedzić nazwą tego arkusza. Tutaj jednak trzeba sięgnąć do opisu konkretnego programu, gdyż sposób prezentacji tak złożonego adresu może się różnić. Np. adres komórki F5 znajdującej się w arkuszu Arkusz3 w programie Calc należałoby zapisać tak: ARKUSZ3.F5, a w programie Excel jako: ARKUSZ3!F5. Taki sam zapis jak w Excelu jest zastosowany w arkuszach Google. Wszystkie arkusze akceptują ujęcie nazwy arkusza w pojedyncze apostrofy i apostrofy te muszą zostać użyte, jeśli nazwa arkusza zawiera spację. Zatem zapis takiego adresu może wyglądać też tak: 'Arkusz3'!F5. Zapis „Arkusz3!A1:B2” określa obszar złożony z komórek „A1”, „A2”, „B1” i „B2” w arkuszu „Arkusz3”.

Z podanych wcześniej wartości granicznych kolumn i wierszy widać, że są to ogromne arkusze, zwłaszcza że tabelkę, która miałaby powiedzmy 10 kolumn i 30 wierszy już uznajemy za dużą. Gdybyśmy zechcieli przedstawić tak zdefiniowane arkusze w postaci tabeli wykreślonej na papierze, w której każda kolumna miałaby 2 cm szerokości a każdy wiersz 0,5 cm wysokości, to potrzebny do tego papier musiałby mieć prawie 328 m szerokości i ponad 5 km długości dla arkusza w Excelu. W arkuszu Google-u byłoby to tylko 5 m szerokości i ponad 8 m długości. Niezłe tabelki!

Z powodu rozmiarów arkusza, ekran komputera nie jest w stanie pokazać go w całości, dlatego widać tylko jego wybrany fragment. Ekran jest czymś w rodzaju ramki, umieszczonej nad ogromnym arkuszem, przez którą widzimy tylko wybraną jego część. Aby ułatwić nam orientację, jaką część arkusza obecnie oglądamy, nad górna krawędzią tej ramki wyświetlone są nazwy kolumn, zaś po lewej stronie wyświetlone są numery wierszy. Widać to na zaprezentowanej poniżej ilustracji, na której arkusz jest widoczny od 82. wiersza kolumny „G”. Podgląd innych części arkusza możliwy jest przez użycie klawiszy ze strzałkami (w lewo, w prawo, w górę, w dół), klawisza tabulacji (TAB, SHIFT+TAB) klawiszy PageUp, PageDown (oznaczonych czasami PgUp i PgDn) lub przy użyciu myszki poprzez wykorzystanie suwaków (pionowego po prawej stronie i poziomego u dołu) i przycisków przy nich się znajdujących. Spowoduje to przesuwanie – trzymając się już tej terminologii – „ramki” nad inną część arkusza.

W arkuszu jedna z komórek jest wyróżniona obramowaniem jej krawędzi odmiennym kolorem. Jest to komórka aktywna, czyli taka której dotyczą podejmowane akcje i polecenia. Jeśli zaznaczony jest obszar, to takie polecenia i akcje dotyczą całego tego obszaru. W zaznaczonym obszarze nadal jednak jedna komórka jest wyróżniona, i z nią związana jest procedura wypełnienia jej treścią. Wspomniane powyżej klawisze strzałek i skróty klawiaturowe, tak naprawdę przenoszą uaktywnienie komórki na kolejną, wynikającą z użytych klawiszy. Jeśli kolejna aktywna komórka znajdowałaby się poza granicą wyświetlania, nastąpi takie przesunięcie arkusza, aby ta nowa komórka aktywna była widoczna. Nieco inaczej działa to w przypadku wykorzystywania suwaków czyli używania myszki. Komórka aktywna się nie zmienia i możemy oglądać dowolny inny fragment arkusza. Aby w takim obszarze uaktywnić wybraną komórkę, wystarczy kliknąć w nią myszką.

Przy korzystaniu z klawiatury warto zapamiętać pewne zasady jej wykorzystywania, gdyż są one wspólne dla wielu programów arkuszowych. I tak: klawisz HOME uaktywnia komórkę w kolumnie „A” bieżącego wiersza. Klawisz END uaktywnia ostatnią komórkę w wierszu, przy czym kolumnę tej komórki wyznacza ten wpis do całego arkusza, który zajmuje najdalszą kolumnę. Skrót klawiaturowy CTRL+HOME – do komórki A1, a CTRL+END – do ostatniej komórki dostępnej w arkuszu, wynikającej z zapisów znajdujących się w najdalszej kolumnie (wyznaczenie kolumny) i najdalszym wierszu (wyznaczenie wiersza). Wykorzystanie klawiszy ze strzałkami z przyciśniętym klawiszem CTRL przenosi aktywność do ostatniej komórki zawierającej ciągłe wpisy w wybranym kierunku albo do pierwszego wpisu w tym kierunku. Aby powrócić do komórki aktywnej w sytuacji gdy arkusz został przewinięty suwakami myszki, należy skorzystać ze skrótu CTRL+BACKSPACE.

Czasami odnalezienie komórki aktywnej jest utrudnione ze względu np. na stosowanie własnych obramowań komórek, podobnych do obramowania komórki aktywnej. Na powyższej ilustracji można zobaczyć, że położenie komórki aktywnej, tutaj „I89”, jest dodatkowo sygnalizowane wyróżnieniem (kolorem lub w inny sposób) na krawędziach zawierających nazwy kolumn i numery wierszy. Specjalne znaczenie odgrywa także, zaznaczony na rysunku, prawy dolny narożnik komórki aktywnej. Będzie o nim mowa w dalszej części. Ponadto w prawie wszystkich programach arkuszowych, nad górnym lewym narożem wyświetlanego fragmentu arkusza, znajduje się małe pole, pole adresu, w którym wyświetlony jest adres komórki aktywnej. Ten element także widać na przedstawionych ilustracjach, z wyjątkiem arkusza Google, dlatego napisałem „prawie we wszystkich”. Okienko to można wykorzystać do wskazania potrzebnej komórki aktywnej, wpisując do niego – zamiast tam widocznego – nowy adres. Wprowadzony adres należy zatwierdzić klawiszem ENTER. Wskaźnik aktywności zostanie przeniesiony do tej wybranej komórki. Jeśli komórka ta nie była dotychczas widoczna na ekranie, zostanie zmieniony wyświetlany fragment arkusza. Przy czym w programie Calc, nowa aktywna komórka znajdzie się w centrum zmienionego wyświetlanego fragmentu, zaś w programie Excel, w prawym dolnym rogu tego fragmentu.

Aby zaznaczyć jakiś obszar w arkuszu przy pomocy klawiatury, należy ustawić komórkę aktywną w dowolnym wybranym rogu planowanego obszaru a następnie trzymając przyciśnięty klawisz SHIFT użyć klawiszy ze strzałkami. Wyznaczony w ten sposób obszar będzie wyróżniał się kolorem. To samo można wykonać myszką. Należy kliknąć pożądany róg planowanego obszaru i nie puszczając lewego przycisku myszy przeciągnąć jej wskaźnik w planowany róg przeciwległy.

Oczywistym jest, że podane przeze mnie rozmiary arkuszy, to ich potencjalne możliwości. Większości zastosowań wystarczy wykorzystanie znacznie mniejszej liczby kolumn i wierszy. Arkusz Google „na dzień dobry” udostępnia 20 kolumn (od „A” do „T”) i 100 wierszy. W trakcie pracy, po osiągnięciu tych granicznych wartości, można dodawać nowe potrzebne kolumny i wiersze. Na ilustracji powyżej widać wygląd dolnej części arkusza, gdy osiągnięty został ostatni, czyli w tym przypadku setny wiersz. Dostępny tam przycisk „Dodaj więcej wierszy”, pozwala uzupełnić arkusz o kolejne wiersze.

Zajmę się teraz praktycznym wykorzystaniem arkusza kalkulacyjnego. Wspomniałem już o tym, że podstawową jednostką arkusza jest komórka. Tabela tworzona przez nas składa się z wielu komórek i tak naprawdę może rozprzestrzeniać się w dowolnej części arkusza. Najczęściej zaczyna się w komórce o adresie A1 a prawy dolny róg wynika z rzeczywistej wielkości projektowanej tabeli.

Wpisy do komórek.

Wszystko co chcemy umieścić w tabeli musimy wprowadzić do odpowiednio położonych komórek. Jeśli do komórki niczego nie wprowadzimy, pozostanie komórką pustą. Jeśli jednak zechcemy coś wpisać, to może to być tylko jeden z czterech rodzajów wpisów:

Wpis tekstowy, czyli dowolny zestaw znaków tworzących jakieś napisy.

Wpis liczbowy, czyli taki zestaw znaków, który zostanie zinterpretowany jako liczba.

Wpis logiczny, czyli informację, że w komórce znajduje się wartość prawdy lub nieprawdy.

Formuła, czyli wpis określający wzór (algorytm) jaki zostanie „obliczony”, i którego wynik zostanie wyświetlony w komórce. Wynikiem formuły nie musi być wyłącznie liczba.

Zasada wpisywania do komórek jest zawsze taka sama. Należy uaktywnić komórkę, do której zostanie dokonany wpis. Jeżeli wpis następować będzie do komórki pustej, albo gdy zastąpić ma dotychczasową zawartość komórki, wprowadzamy z klawiatury potrzebny tekst i zatwierdzamy go klawiszem ENTER. Nowo wpisane znaki zastąpią te, który były w komórce wcześniej. Nie musimy zatem niczego wcześniej kasować. Jeśli chcemy poprawić zawartość komórki, gdyż w długim wpisie zauważyliśmy błędy i nie chcemy tego wpisu ponownie wprowadzać w całości, należy nacisnąć klawisz funkcyjny F2. Program umieści kursor tekstowy na ostatnim znaku treści, bezpośrednio w komórce. Klawiszami strzałek (w lewo, w prawo) można przenosić ten kursor do dowolnego miejsca w treści i poprawiać ją, tak jak w edytorze tekstowym. Mówimy wówczas o edycji komórki. Zatwierdzenie zmian, także klawiszem ENTER.

Tutaj muszę dodać uwagę związaną z używanymi przeglądarkami. Arkusz Google wykorzystuje do obsługi klawisze funkcyjne (F1 do F12) w taki sam sposób jak przyjęto ich używać w Excelu. Niektóre przeglądarki mogą jednak używać tych klawiszy do realizacji własnych akcji i wówczas zostanie wybrana funkcja przeglądarki, a nie arkusza kalkulacyjnego a nawet obie na raz (np. w przeglądarce Opera, klawisz F2 służy do przechodzenia do innej strony WWW, nie może więc zostać użyty do edycji komórki).

Możliwość edytowania wpisu w komórce pojawi się także po dwukrotnym kliknięciu komórki myszką lub po jednokrotnym kliknięciu w pole wiersza wprowadzania i edytowaniu wpisu w tym właśnie polu. Pole wiersza wprowadzania znajduje się zazwyczaj bezpośrednio nad nazwami kolumn i pokazuje zawsze treść wpisaną do aktualnie aktywnej komórki.

Na ilustracji powyżej pokazany jest fragment arkusza z widocznym wierszem wprowadzania. Czytelnik powinien zwrócić uwagę na to, że wiersz wprowadzania pokazuje zawsze wpis wprowadzony do komórki, komórka natomiast – efekt tego wpisu. W tym przypadku do komórki wpisano formułę i jej treść widać w wierszu wprowadzania, gdy tymczasem komórka pokazuje wynik tej formuły. Tryb edycji komórki aktywnej w arkuszu Google uzyskamy także, naciskając klawisz ENTER.

Aby usunąć zawartość komórki, czyli spowodować, że będzie ponownie pusta, należy po jej uaktywnieniu nacisnąć klawisz DELETE. Jeśli klawisz DELETE naciśnięto gdy zaznaczony był jakiś obszar w arkuszu, usunięta zostanie zawartość wszystkich komórek w tym zaznaczonym obszarze.

Zobaczmy przykładowe zestawienie dotyczące sprzedaży czasopism poświęconych komputerom. W ostatniej dekadzie XX wieku to były główne tytuły związane z tą tematyką.

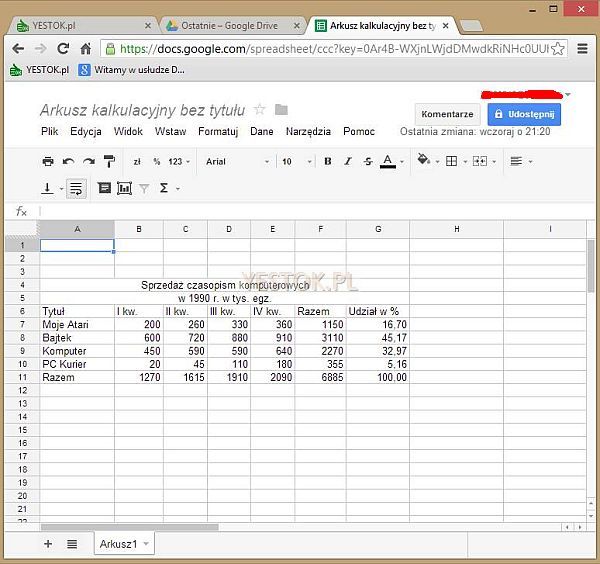
Przedstawione zestawienie zawiera puste trzy pierwsze wiersze a następnie wpisy tekstowe w wierszu 4, 5 i 6-tym oraz w obszarze „A7:A11”,wartości liczbowe w obszarze „B7:E10” i formuły w obszarach „F7:G10” i „B11:G11”. Jak widać nie musi zaczynać się w komórce „A1”. Pojęcie formuły wyjaśnię na przykładzie komórki „F7”. Komórka ta powinna zawierać sumaryczną liczbę sprzedanych egzemplarzy czasopisma „Moje Atari”. Autor zestawienia mógłby oczywiście dodać do siebie liczby podane dla poszczególnych kwartałów i wpisać liczbę 1150. Gdyby jednak okazało się, że w kwartale II i IV sprzedano inną liczbę egzemplarzy, musiałby wpisać nowe wartości dla tych kwartałów, ponownie zsumować liczby i podać nową, zmodyfikowaną wartość. Formuła jest algorytmem (wzorem) podającym jak należy wyznaczyć informację wyświetlaną w komórce, w tym przypadku w komórce F7. Wpisana tam formuła może mieć postać „=B7+C7+D7+E7” lub „=SUM(B7:E7)”. W pierwszym wariancie operatorami dodawania połączone są adresy komórek, których zawartość ma zostać dodana do siebie. W drugim przywołano funkcję o nazwie SUM wskazując tej funkcji obszar komórek, które mają być zsumowane. W komórce G7 wpisano formułę „=F7/F11*100”, która wylicza procentowy udział sprzedaży „Mojego Atari” wobec wszystkich podanych tytułów. Formuła ta powiada bowiem, że w komórce G7 ma być wyświetlony wynik dzielenia zawartości komórki F7 przez zawartość komórki F11, pomnożony przez liczbę 100, a tak właśnie wylicza się udział procentowy. Jeśli podobnie zbudowane formuły zostaną wpisane do pozostałych komórek, to zmiany wprowadzane w obszarze wartości, czyli w obszarze „B7:E10”, będą automatycznie powodowały wyświetlanie nowych wartości w komórkach zawierających formuły. I to jest tak naprawdę podstawa funkcjonowania arkuszy kalkulacyjnych.

Wpis tekstowy.

Standardowo wpisy tekstowe rozpoczynają się od lewej krawędzi komórki. Arkusze kalkulacyjne same próbują zinterpretować rodzaj wpisu i najczęściej nie mają problemu z rozpoznaniem tekstu. Istnieją jednak sytuacje, w których treść wpisywana do komórki ma być tekstem, chociaż wygląda jak liczba, np. gdy wpisujemy NIP, REGON lub numer telefonu. W takich sytuacjach jako pierwszy znak należy wpisać apostrof i dopiero po nim potrzebne dane. Excel i arkusz Google zawsze interpretują pierwszy apostrof jako informację, że wprowadzane znaki mają zostać potraktowane jak tekst, i w komórce ten apostrof nie jest wyświetlany. Calc uznaje apostrof za informację, że wprowadzane dalsze znaki są tekstem tylko wtedy, gdy te dalsze znaki zinterpretuje jako liczbę. Zatem wpisanie do komórki ciągu „’123” zostanie potraktowane we wszystkich tych programach jako tekst i w komórce wyświetlona zostanie zawartość „123”, już bez apostrofu i dosunięta do lewej krawędzi komórki. Wpisanie natomiast ciągu „’abc” wyświetli ciąg „abc” w Excelu i arkuszu Google ale „’abc” w Calcu.

Wpisy tekstowe mogą być różnej długości. Dopuszczalna długość wprowadzanego tekstu jest na tyle duża, że nie musimy się zastanawiać czy cały tekst się zmieści w komórce. Problemem jest ile z tego wprowadzonego tekstu wyświetli się w komórce wtedy gdy szerokość komórki jest za mała. I tutaj programy zachowują się różnie. Arkusz Google spróbuje zawinąć linijkę tekstu w taki sposób aby go wyświetlić w całości. Spowoduje to oczywiście zwiększenie wysokości komórki. Sam tekst jest zawijany na granicach wyrazów, zatem jeśli pojedynczy wyraz nie zmieści się w szerokości komórki, to część wykraczająca poza granicę komórki nie zostanie wyświetlona.[usunięte listopad 2014] Od końca roku 2013 dostępna jest już Nowa wersja Arkuszy Google. Do końca roku 2015 ma zostać dokonana migracja wszystkich arkuszy do tej nowej wersji a obecnie tworzone arkusze powstają już tylko w tej nowej wersji. Pod względem wpisów tekstowych arkusz ten zachowuje się teraz tak jak pozostałe. Więcej informacji znajduje się w systemie pomocy Google.[dodane w listopadzie 2014] W pozostałych arkuszach tekst wpisany do komórki wyświetlany jest w niej, oraz poza nią, na tle sąsiadujących kolejnych komórek, jeśli są puste. Trzeba tu powiedzieć, że tekst wpisany do komórki jest w niej zapamiętany bez względu na to ile z tego tekstu jest widoczne w komórce. W przedstawionym przykładzie tekst „Sprzedaż czasopism komputerowych” był na tyle długi, że aby uniknąć zawijania go w komórce „A4”, scaliłem komórki od „A4” do „G4”, tworząc jedną szeroką komórkę, a w niej tekst ten mieści się całkowicie. Takie scalone komórki mają adres tożsamy z adresem lewego górnego rogu scalanego obszaru. Wykorzystałem tu także możliwość wyrównania tekstu wewnątrz komórki, wybierając polecenie umieszczenia go w środku komórki. Analogicznie postąpiłem z zawartością wiersza piątego.

Wpis liczbowy.

Ten rodzaj wpisu naturalnie kojarzymy z liczbami. Wszelkie wpisane znaki zostaną potraktowane jako wpis liczbowy, jeśli mogą zostać prawidłowo potraktowane jako liczba. Jeśli tak nie będzie, zostaną potraktowane jako wpis tekstowy. Znakiem dziesiętnym liczby, czyli znakiem oddzielającym część ułamkową od części całkowitej jest znak wynikający z ustawień regionalnych systemu operacyjnego. W Polsce jest to znak przecinka. Ważny jest także przyjęty znak separatora tysięcy, czyli znak oddzielający trzycyfrowe ciągi w wielkich liczbach. W ustawieniach regionalnych dla Polski tym znakiem jest spacja. Dlatego liczba 8012345,67 może być także przedstawiona jako 8 012 345,67 co znacznie ułatwia jej odczytanie. Ta sama liczba w USA przedstawiona mogłaby być jako 8,012,345.67 gdyż tam znakiem separującym jest przecinek a kropka znakiem dziesiętnym. Tutaj mała dygresja dotycząca klawiatury komputera. Część numeryczna klawiatury, znajdująca się po prawej stronie, zawiera naniesiony znak kropki. Klawisz ten wprowadza jednak podczas pisania znak, który przypisany jest we wspomnianych ustawieniach regionalnych jako znak dziesiętny. W przypadku Polski jest to więc przecinek. Uwaga ta dotyczy także używania klawiatury numerycznej w komputerach przenośnych, w których ta klawiatura naniesiona jest odrębnym kolorem na alfanumerycznej części klawiatury podstawowej.

Liczby mogą być poprzedzane znakami +(plus) albo –(minus), jednak po zaakceptowaniu wpisu tylko znak minus będzie wyświetlony z liczbą. Wprowadzone zera poprzedzające liczbę zostaną usunięte, chyba że jest to ostatnie zero przed przecinkiem dziesiętnym. Jeśli wprowadzone zostaną prawidłowe znaki separatorów tysięcy to wpis zostanie zaakceptowany jako liczba, jednak separatory te zostaną z liczby usunięte. Wszystkie liczby zostaną w komórce dosunięte do jej prawej krawędzi.

W obliczeniach czasem pojawia się problem liczb bardzo dużych albo bardzo małych. Arkusz Google pozwala wprowadzić liczbę złożoną z 15 cyfr. Jeśli liczba będzie miała więcej niż 15 cyfr przed przecinkiem, zostanie potraktowana jak tekst. Generalnie, liczba wprowadzona w Arkuszu Google może składać się z 15 cyfr, uwzględniając te przed i te po przecinku. Czym więcej cyfr przed przecinkiem, tym mniej może ich być po przecinku. Arkusz kalkulacyjny Google został opracowany przede wszystkim z myślą o obliczeniach ekonomiczno-biznesowych i w tym zakresie ten sposób przechowywania liczb spełnia swoją rolę.

Ci czytelnicy, dla których matematyka nie była czarną magią, pamiętają zapewne sposób zapisu liczb z wykorzystaniem wykładnika potęgi liczby 10. Pozwala on na zapisanie liczb bardzo dużych np. 150 000 000 jako 1,5×10⁸ albo bardzo małych jak 8,854187817×10^-12 (to jest akurat wartość przenikalności elektrycznej próżni). W arkuszach kalkulacyjnych rolę podstawy potęgi 10 odgrywa litera „E” (mała lub wielka) zatem te same liczby wpisywać można do nich jako „1,5E8” albo „8,854187817e-12”. Tego typu liczby dotyczą jednak w większości zastosowań w obliczeniach naukowych. Dlatego w Arkuszu Google są stosunkowo słabo rozpracowane. Druga z wprowadzonych liczb zostanie zapamiętana jako 0,000000000008854. Cyfra 4 jest piętnastą cyfrą po przecinku. Pozostałe cyfry zostały – jak widać – pominięte. Zdecydowanie lepiej wygląda to w Excelu i Calcu.

Wprowadzona do komórki liczba jest zawsze pamiętana z maksymalną dopuszczalną w danym arkuszu dokładnością bez względu na to w jaki sposób jest wyświetlona. To, jak liczby mają być wyświetlone, jest odrębnym zagadnieniem i będzie o tym mowa w dalszej części.

O liczbach niekonwencjonalnie.

Liczby traktujemy zazwyczaj jako wynik liczenia, wyrażenie pewnej wartości arytmetycznej. Liczba może jednak też obrazować stan liczebny (w opakowaniu jest 12 słoiczków), oznakowanie symboliczne (zadanie wykonał na 5) lub zależność porządkową (zajął w zawodach 3 miejsce). Wszystkie te informacje prezentowane są za pomocą cyfr. Arabskich (0-9) ale także liczb rzymskich (Benedykt XVI). Arkusze kalkulacyjne nie działają oczywiście na liczbach rzymskich, ale potrafią przedstawić liczbę arabską jako rzymską i odwrotnie.

Rozdział ten poświęcam jednak specyficznemu użyciu liczb, które mogą być, albo będą, traktowane jak prezentacja daty i godziny.

We wszystkich arkuszach przyjęto, że datę prezentować będzie liczba całkowita, i będzie to liczba dni jakie upłynęły od pewnego umownego dnia w przeszłości. W przypadku Arkusza Google jest to 30. grudzień 1899 roku. Podobnie w Calcu, w Excelu tą datą jest 1. styczeń 1900 roku. Zatem liczba 1 może zostać potraktowana w Arkuszu Google jako 31 grudzień 1899 roku. Zgodnie z tym data, np. 1 maja 2013 roku to liczba 41395 i o takiej liczbie powiemy, że jest to liczba daty. Nikt oczywiście nie jest w stanie znać takich liczb dla każdej daty. Dlatego wprowadzenie do komórki ciągu cyfr zgodnego z zasadami wpisywania daty, wprowadzi do komórki właściwą liczbę, przy czym komórka zmieni sposób prezentowania tej liczby na taki aby była to prezentacja tej daty. Dla podanej daty 1. maja 2013 roku można do komórki wpisać następujące ciągi „2013-05-01”, „1-5-2013”, „1/5/2013” czy „2013/5/1” a zostaną one zamienione na właściwą liczbę daty. Arkusz kalkulacyjny interpretując wprowadzany ciąg, zmieni także sposób prezentowania tej liczby, i będzie ona przedstawiona jako „2013-05-01” a więc w sposób czytelny dla użytkownika arkusza. Sposób prezentowania liczby ustalany jest przez polecenia nazywane „formatowaniem komórki”. Będzie o tym mowa w dalszej części. Tutaj to „formatowanie” zostało zastosowane automatycznie. Musimy jednak pamiętać, że niezależnie od prezentowania zawartości komórki, zawiera ona zawsze pewną wartość pierwotną, taką jaka została wprowadzona przez użytkownika lub wyliczona.

Dzięki przedstawianiu dat jako liczb, łatwo jest obliczać różnicę dni między datami, wyznaczać daty przyszłe lub przeszłe. Wystarczy dodawać lub odejmować wymaganą liczbę dni lub odejmować daty od siebie. Liczby ujemne traktowane są jako daty poprzedzające tę umowną granicę. Nie dotyczy to Excela, który nie dopuszcza liczb ujemnych jako prezentacji daty.

W przypadku czasu i jego prezentacji w arkuszach przyjęto, że konkretny moment będzie zapamiętywany jako ułamek. Wartość 0,0 odpowiada godzinie 0:00:00, wartość 0,5 odpowiada godzinie 12:00:00 a np. wartość 0,33333333 odpowiada godzinie 8:00:00. Wprowadzanie do komórki ciągu np. „7:55” zostanie zinterpretowane jako wprowadzanie godziny i zamienione na ułamek 0,329861111111111. Jednocześnie prezentacja zawartości tej komórki zostanie automatycznie zmieniona na taką aby użytkownik widział godzinę wyświetloną jako „07:55:00”.

Podsumowując, dowolna liczba może być traktowana jak data łącznie z czasem. Jeśli podsumowanie naszego rachunku wyniosło 235,56 zł, to możemy przy pomocy formatowania zażądać wyświetlenia tej liczby jako daty i godziny. W tym wypadku otrzymalibyśmy „1900-08-22 13:26:24”.

Wpis logiczny.

Poza tekstami i liczbami arkusze kalkulacyjne rozróżniają jeszcze jeden rodzaj wpisu, wpis wartości logicznej. Na etapie poznawania arkusza jest to wpis raczej abstrakcyjny, ale dla porządku także go tutaj wymienię. Tym wpisem jest wartość określona jako TRUE lub FALSE. Wartości te w arkuszach Excel i Calc mają określenie PRAWDA lub FAŁSZ. Wpisanie do komórki takiej treści jest traktowane jako wstawienie odpowiadającej temu wpisowi wartości logicznej a nie tekstu TRUE lub FALSE. Aby wstawić ten wpis jako tekst, należałoby poprzedzić go apostrofem. Napis może zostać dowolnymi literami, i tak zostanie zamieniony na odpowiadającą wartość, prezentowaną wielkimi literami.

Następna część opracowania poświęcona jest dwóm tematom:

• Prezentacji zawartości komórek. A więc przedstawianiu konkretnych wyników liczbowych oraz różnicowaniu ogólnego wyglądu komórek.
• Omówieniu problematyki budowania formuł.