Yestok.pl

Opracowanie powstało w oparciu o wersję programu Word 2007.

We wszystkich opracowaniach dotyczących nauk ścisłych, technicznych, inżynierskich czy ekonomicznych pojawia się potrzeba zamieszczenia w treści pracy równania a bardzo często wielu równań będących nieodłączną częścią opracowania. Zaawansowane edytory tekstów umożliwiają przygotowanie i umieszczenie w tekście obiektu, który może wyglądać np. tak:

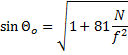
Takie rozwiązanie ma także pakiet MS Office. Do wersji Office 2003 funkcje edytora równań pełnił dodatek do oprogramowanie o nazwie Equation, ostatnia znana mi wersja to 3.1. Edytowanie równania w wybranym miejscu odwoływało się do oddzielnego modułu programowego i tworzenie równania następowało w tym niezależnym module. Zakończenie edycji było równoznaczne z opuszczeniem modułu i powrotem do edytora Word. Efekt pracy modułu to umieszczony w dokumencie macierzystym obiekt „równanie”. Tego obiektu nie można było edytować w Wordzie, można go było jednak przetwarzać tak jak obiekt graficzny. Dwukrotne kliknięcie obrazu równania ponownie przywoływało moduł Equation i można było wprowadzać niezbędne poprawki.

Od Office w wersji 2007 funkcjonuje nowy edytor równań (Equation Editor), który stał się integralną częścią edytora Word i funkcjonuje według innych zasad. Równanie nie jest teraz obiektem, lecz samodzielną strukturą Worda. Z tego powodu, jeśli oprogramowanie pracuje w trybie zgodności, czyli otwarto w nim dokument z wersji starszej niż 2007, wstawianie równań tym edytorem nie jest możliwe. Word w wersji 2007 zachował możliwość używania starego edytora równań. Nie wdając się w teoretyczne aspekty, równanie może być modyfikowane tylko tym edytorem, jakim zostało wcześniej utworzone. Jeśli dokument z równaniami starszej wersji został przekonwertowany do wersji nowej, to stare równania można edytować tylko korzystają z Equation a nowe można skonstruować zarówno starą jak i nową metodą. Jeśli dokument Worda 2007 lub nowszego został zapisany w starszym standardzie dokumentu (97-2003) to równania skonstruowane nowym edytorem zostaną przekształcone w obiekt graficzny i nie będą mogły być modyfikowane w ogóle. Możliwość ich modyfikacji powróci po przekonwertowaniu dokumentu do standardu zapisu obowiązującego od wersji 2007.

Niezależnie od rozwiązań zaimplementowanych w Wordzie jedna z firm – Disign Science – od wielu lat oferuje rozwiązanie pod nazwą Math Type, które integruje się z edytorem Word i pozwala tworzyć i edytować równania w bardzo rozbudowanym zakresie. Oprogramowanie to jest dobrze oceniane przez użytkowników a jego najpoważniejszą „niedogodnością” jest konieczność zakupu licencji. Oprogramowanie w wersji „trial” można pobrać ze strony producenta http://www.dessci.com/en/products/mathtype/trial.asp . W tej wersji będzie ono w pełni funkcjonalne przez 30 dni. Po tym okresie, jeśli użytkownik nie zdecyduje się na zakup, przejdzie do wersji „lite”, która odpowiada wbudowanemu do Worda edytorowi równań (czyli Equation 3.x), pozostawiając jednak dodatkowe czcionki i symbole, co niektórzy użytkownicy uważają i tak za korzystniejsze niż używanie standardowego starego edytora. Na stronie producenta sytuacja ta wyjaśniona jest następująco:

You will have 30 days in which to enjoy all of the features of MathType. If you do not purchase MathType within 30 days, it will become MathType Lite. This is exactly like Equation Editor, with the bonus of MathType's fonts and symbols, which you may use with our compliments.

Nie sposób w tym miejscu nie wspomnieć o całkowicie odmiennym podejściu do edycji dokumentu opartym o środowisko LaTeX. To środowisko programistyczne jest bardzo cenione przez grupy zawodowo zajmujące się edycją. Jego pierwsze wydanie pojawiło się w 1985 roku. Właśnie w tym środowisku pojawił się język znaczników pozwalający konstruować równania matematyczne. Ten język i jego składnia, a przynajmniej logika, zostały w wielu przypadkach przyjęte przez inne systemy tworzenia i edycji równań w tym także w MathType i Wordzie.

Pod adresem https://latex.codecogs.com/eqneditor/editor.php?lang=pl-pl znajduje się internetowy edytor równań matematycznych online. Obraz utworzonego równanie można zapisać w pliku i umieścić w dokumencie w potrzebnym miejscu.

To opracowanie poświęcone jest jednak standardowemu edytorowi równań wbudowanemu do programu Word od wersji 2007. Dla osób, które z koniecznością wstawiania do opracowania wzorów matematycznych spotkają się sporadycznie, np. przy okazji napisania pracy licencjackiej, edytor ten jest bardzo przyjazny gdyż budowa równania odbywa się w sposób całkowicie intuicyjny. Nie oznacza to oczywiście tego, że edytor ten ma jakieś ograniczenia, wręcz przeciwnie jego możliwości są w stanie spełnić oczekiwania bardzo wymagających autorów. Jednak i tutaj Microsoft nie do końca sprostał oczekiwaniom użytkowników. Tworząc nowe oprogramowanie do edycji równań nie rozwiązał problemu trapiącego użytkowników Equations 3.x, czyli braku automatycznego numerowania wstawianych równań, co w opracowaniach, w których równania są zasadniczym elementem dokumentu jest bardzo potrzebne. Jak to napisał w swoim serwisie internetowym Andreas Rejbrand [ http://english.rejbrand.se/rejbrand/msword.asp, dostęp 18.07.2015]

This is all very sad. The new formula editor in Microsoft Word 2007 and later is awesome, but it clearly lacks a very important feature. It is almost like designing a really luxurious car, and forgetting to add doors to it.

Nawiasem mówiąc bardzo polecam to opracowanie – i cały serwis – tym, którzy piszą zaawansowane prace z dziedziny nauk ścisłych.

Użytkownicy Worda znaleźli oczywiście metodę na numerowanie równań i choć jest to tylko proteza, to w dokumencie wygląda dobrze. O tym problemie i jego rozwiązaniu napiszę w dalszej części.

Wstawianie równań i wzorów do dokumentacji podlega także pewnym normom, których należałoby przestrzegać a przynajmniej o nich wiedzieć. Może trafić się opiekun, promotor lub redaktor opracowania, który będzie zwracał uwagę na każdy szczegół. Warto więc zapoznać się na przykład z opracowaniem profesora Krystyna Pawluka, przewodniczącego Polskiego Komitetu Terminologii Elektrycznej, o tym „Jak pisać teksty techniczne poprawnie”, albo Edwarda Musiała, poświęconego pisowni oraz wymowie nazw jednostek miar. Opracowania te dostępne są na stronach Stowarzyszenia Elektryków Polskich http://www.sep.com.pl [dostęp:15.07.2015] w zakładce Opracowania.

Zanim zajmę się właściwymi równaniami pokażę, jakiego rodzaju obiektem jest ta konstrukcja. Poniżej na ilustracji przedstawiłem to samo równanie w trzech sytuacjach. Lewa strona Ilustracji pokazuje stan równania tak, jak wygląda ono w dokumencie, część środkowa – to stan tego obszaru po naprowadzeniu nań wskaźnika myszki i w końcu część prawa – to ten sam obszar po kliknięciu weń myszką.

Prawa część ilustracji mogłaby sugerować, iż jest to obiekt w rodzaju kształtu, jednak tak nie jest. Obiektu tego nie można powiększyć chwytając go za brzeg albo naroże. Nie można go także umieścić w dowolnym miejscu strony, musi być częścią akapitu. Edycja równania jest możliwa gdy mamy do czynienia z tą trzecia postacią. Równanie jest blokiem symboli oraz oznaczeń literowych i cyfrowych odpowiednio rozmieszczonych względem siebie, będącym obiektem matematycznym, traktowanym przez Worda jak element tekstu. O tym świadczy środkowa część ilustracji wyróżniająca obszar zajęty przez tę konstrukcję, jako odrębną jednostkę akapitu. Aby przejść do możliwości edytowania równania wystarczy, jak wspomniałem, kliknąć myszką w dowolne miejsce w tym obszarze.

Rysunek 2., poniżej, pokazuje stan bloku równania po kliknięciu w prawy margines tego bloku, co spowodowało rozwinięcie menu z poleceniami dotyczącymi równania. Taki stan bloku został pokazany na ilustracji.

Przeciągnięcie równania w inne miejsce dokumentu jest możliwe jedynie przy pomocy lewego górnego uchwytu (zaznaczony na ilustracji) i można je wykonać tylko w obszarze tekstu.

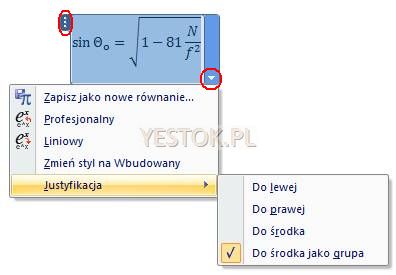
Polecenia dostępne w menu dotyczą całego równania i mają następujące znaczenie:

„Zapisz jako nowe równanie…” – pozwala zapisać utworzone równanie i wykorzystać je w przyszłości w innych opracowaniach. Równanie nie jest jednak zapisywane, jako oddzielny plik, co sugerować mogłaby ikona dyskietki, lecz jako blok konstrukcyjny Worda. Bloki konstrukcyjne to zagadnienie stosunkowo słabo znane większości użytkowników. Ten temat także omówię w dalszej części opracowania.

Dwa polecenia wzajemnie się wykluczające: „Profesjonalny” i „Liniowy” decydują o sposobie prezentowania równania w dokumencie. Dla zobrazowania różnicy proszę spojrzeć na rys. 3. Przedstawia on to samo równanie, pokazane w sposób profesjonalny (powyżej) i liniowy (poniżej).

Liniowa postać równania ma w założeniu zapewnić możliwość umieszczenia równania w treści akapitu, jest jednak dużo trudniej czytelna niż postać profesjonalna. Wiedza o liniowej postaci równania może być jednak przydatna, bowiem edytor równań akceptuje wpisanie równania w tej postaci i może przekształcić je w postać profesjonalną. Wprawieni użytkownicy dużo szybciej i sprawniej utworzą równania tym sposobem.

Justyfikacja – pozwala wybrać sposób wyrównania bloku równania względem marginesów i jest w gruncie rzeczy poleceniem podręcznym, realizującym znane z edycji tekstów „Wyrównaj tekst do lewej” (CTRL+l), „Do środka w poziomie” (CTRL+e) i „Wyrównaj tekst do prawej” (CTRL+r). Jedynie ostatnia opcja – „Do środka jako grupa” – funkcjonuje inaczej i zostanie omówiona w dalszej części, ma ona bowiem znaczenie wtedy gdy prezentowany jest układ kilku równań.

Pozostaje jeszcze jeden aspekt dotyczący równania – jego umiejscowienie w tekście. Położenie w dokumencie określone jest jednym z dwóch stylów równania. Na rysunku powyżej, wśród wyświetlonych poleceń widoczne jest polecenie „Zmień styl na Wbudowany”, co sugeruje, że równanie ma aktualnie inny styl a tym alternatywnym jest właśnie „Wbudowany”. Zasadniczo w pracach naukowych równanie umieszczane jest w oddzielnym akapicie i blok równania jest jedynym elementem takiego akapitu. Blok równania standardowo jest wyśrodkowany, lecz jego wyrównanie można zmienić zgodnie z ustawieniami polecenia „Justyfikacja”. Takie położenie bloku ma przypisany styl „Wyświetlanie”.

Równanie można również utworzyć wewnątrz akapitu. Blok takiego równania staje się częścią wiersza i podlega regułom zgodnym z obowiązującymi w akapicie. W tak ulokowanym równaniu opcja „Justyfikacja” jest już niedostępna gdyż samego równania nie można już wyrównywać, jest ono wyrównywane przez ustawienia akapitu. Takie położenie bloku ma przypisany styl „Wbudowany”.

Rozwijane menu, takie jak pokazane na rys. 2., zawsze zawiera polecenie zmiany stylu równania na taki, jaki jest w opozycji do aktualnie przypisanego.

Jeśli równanie ma przypisany styl „Wbudowany”, czyli znajduje się w treści akapitu i styl ten zostanie zmieniony na „Wyświetlanie”, to akapit zostanie podzielony znakami „miękkiego entera” (SHIFT+ENTER) w taki sposób, aby równanie stanowiło oddzielny wiersz w tym akapicie. Tu pojawia się jedyne odstępstwo od zasady obowiązującej w akapitach, w których tekst zawiera „miękkie entery”. W zwyczajnym akapicie każda zmiana wyrównania tekstu wpływa na wszystkie wiersze tego akapitu, „miękkie entery” nie są bowiem znakami kończącymi akapit. Gdy jednak w oddzielnym wierszu pojawi się równanie to wiersz ten nie bierze udziału w wyrównywaniu akapitu ani wyrównanie równania nie wpływa na pozostałą część akapitu.

Przeciągnięcie równania „wbudowanego” do pustego akapitu zmienia styl równania na „Wyświetlanie” i analogicznie, przeciągnięcie równania „wyświetlanego” do wnętrza akapitu zmieni styl równania na „Wbudowany”. W związku z takim funkcjonowaniem zmiany stylu równania wystarczy, że poza blokiem równania albo przed nim dopiszemy jakikolwiek znak, aby Word uznał, że równanie znajduje się w akapicie zawierającym tekst i zmienił jego styl na „Wbudowany”. To między innymi z tego powodu nie można bezproblemowo wprowadzić numerowania równań.

Wstawianie równań do dokumentu.

Za wstawianie równań odpowiada ikona „Równanie” znajdująca się w grupie „Symbole”, zakładki „Wstawianie”. W zależności od możliwości wyświetlania wstążki programu Word ikona ta może przyjmować wygląd różniący się od tego, jaki pokazany jest na rysunku poniżej.

Reakcja na kliknięcie ikony zależy od tego czy kliknięto górną, jaśniejszą jej część, czy dolną, ciemniejszą, albo trójkątny znacznik z wierzchołkiem skierowanym w dół.

Kliknięcie dolnej części (znacznika) rozwinie listę dostępnych, wcześniej zdefiniowanych równań, które można wstawić od razu do dokumentu bez konieczności indywidualnego redagowania, a które można potem przeredagować zgodnie z własnymi potrzebami. Taką rozwinięta listę przedstawia rysunek poniżej.

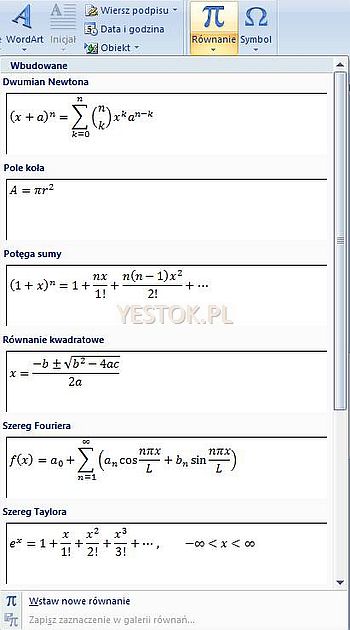
Na takiej liście mogą znaleźć się również równania uprzednio zapisane poleceniem „Zapisz jako nowe równanie…”.

Całkowicie nową formułę można utworzyć trzema metodami. Po kliknięciu górnej części ikony „Równanie” albo, jeżeli rozwinięta została lista, jak ta powyżej, po wybraniu pozycji „Wstaw nowe równanie”. Trzecim sposobem jest przejście do tworzenia równania w dowolnym momencie edycji dokumentu (bez korzystania z zakładki „Wstawianie”) po użyciu skrótu klawiaturowego „ALT+=”. Dowolne z tych działań spowoduje pojawienie się nowej dedykowanej zakładki nadrzędnej „Narzędzia równań”, której przyporządkowana jest jedna zakładka narzędziowa zatytułowana „Projektowanie”. Obraz tej zakładki, (w dwóch częściach) przedstawiam poniżej.

Natomiast w wybranym miejscu pojawi się, przygotowany do wprowadzenia formuły, pusty blok z zachętą do rozpoczęcia edycji. Taki jak poniżej:

Zależnie od tego gdzie znajdował się kursor tekstowy, blok równania będzie miał przypisany styl „Wyświetlanie” albo „Wbudowany”.

Tworzenie równań z wykorzystaniem zakładki „Narzędzia równań”.

Zakładka projektowanie ma trzy grupy narzędzi: „Narzędzia”, „Symbole” i „Struktury”. Polecenia znajdujące się w tych grupach pozwalają na tworzenie i edytowanie równań.

Grupa „Narzędzia” zawiera omówione już polecenia zamiany równania na postać liniową albo profesjonalną, rozwijaną listę „Równanie” wyświetlającą zdefiniowane wcześniej równania wbudowane, oraz przycisk polecenia: „Normalny tekst”. Użycie tego przycisku włącza lub alternatywnie wyłącza wyróżnienie tego polecenia. Włączenie oznacza, że wszelkie wpisywane teksty będą traktowane, jako zapisy niepodlegające regułom automatycznego formatowania równań, choć będą znajdowały się w bloku równania.

Grupa „Symbole” składa się z kilku rozwijalnych list symboli oraz oznaczeń, zorganizowanych w zestawy, i pozwala na wybór symbolu wymaganego w równaniu. Rysunek poniżej prezentuje wszystkie zestawy symboli, jakie można wykorzystać podczas tworzenia równania.

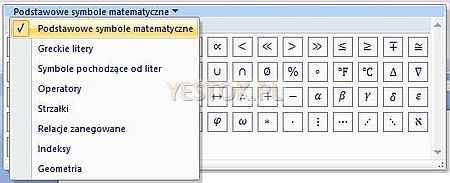
Ostatnią grupę stanowi grupa „Struktury” zawierająca rozwijane listy szablonów różnych struktur tworzących równania. Charakter tych struktur obrazują ikony wyświetlane w tej grupie. Jako przykładu ilustrującego taką listę rozwinąłem strukturę „Nawias”.

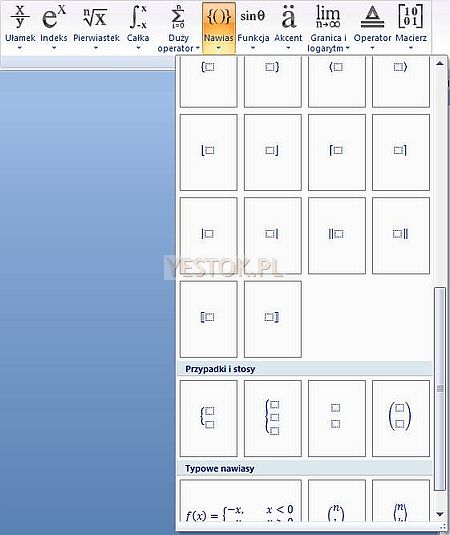
Wybór struktury z takiej listy umieszcza jej szablon w równaniu we wskazanym miejscu. Każdy wykropkowany symbol w szablonie to tak zwany symbol zastępczy reprezentujący składnik struktury, który należy zastąpić właściwym wpisem. Tym wpisem mogą być rozbudowane wyrażenia równania w tym także kolejne struktury.

Budowanie równania z wykorzystaniem symboli i struktur jest w znacznym stopniu intuicyjne i w przypadku równań mniej złożonych nie powinno przysparzać kłopotów. Przypomina to układanie klocków tworzących konstrukcje całego równania. Podczas tworzenia równania symbole zastępcze zastępowane są właściwymi zapisami bezpośrednio z klawiatury. Budując konstrukcję równania nie musimy oczywiście znaków operatorów arytmetycznych czy operatorów porównania pobierać z grupy „Symbole”, można je wpisywać z klawiatury. Edytor równań sam interpretuje wstawiane elementy, dobiera ich kształt i wielkości oraz odstępy między nimi tak, że w zasadzie podczas tworzenia równania nie używamy klawisza spacji. Symbole zastępcze, które nie zostaną zastąpione wpisami nie pojawiają się na wydruku.

Poniższa prezentacja pokazuje utworzenie przykładowego równania, tego z ilustracji na rys. 3, metodą wykorzystania poleceń znajdujących się w zakładce „Projektowanie”.

Prezentacja po konwersji. Naprowadź myszkę na ten tekst aby przeczytać uwagę.

Taki sposób budowania równania jest jednak pracochłonny. Dlatego autorzy często wstawiający równania do swoich prac korzystają z innego, tak zwanego linearnego tworzenia równania, bazującego na wspomnianej już liniowej postaci równania. Edytor najczęściej, bo można taką możliwość wyłączyć, automatycznie przekształca postać liniową na profesjonalną już w trakcie pisania.

Zanim napiszę o tym sposobie warto poznać kilka uwag ogólnych gdyż o ile konstrukcja powstającego równania zależy tylko od inwencji autora, to jego edycja podlega już pewnym regułom obowiązującym w obszarze obiektu matematycznego:

• Do konstruowania równań edytor wykorzystuje czcionkę „Cambria Math” zawierającą niezbędne symbole matematyczne.
• Rozmiar zastosowanej czcionki jest określany na podstawie właściwości stylu akapitu, w którym będzie powstawało równanie. Rozmiar czcionki decyduje o fizycznej wielkości równania.
• Obiekt matematyczny jest częścią akapitu, można mu zatem przypisać odrębny rozmiar czcionki, tak jak to można zrobić z każdym oddzielnym wyrazem wewnątrz akapitu.
• Zmiana rozmiaru czcionki wewnątrz równania, nawet bez zaznaczania czegokolwiek, zmienia wielkość czcionki w całym równaniu. Indywidualnie można zmienić czcionkę i jej rozmiar tylko w miejscach o statusie „Normalny tekst”, jednak każda następna zmiana rozmiaru czcionki równania, ujednolici go w całym równaniu.
• W obszarze równania przedstawianym w postaci profesjonalnej można zaobserwować wewnętrzne bloki rozpoznawane przez edytor matematyczny podczas ich edycji, pojawiają się one także podczas tworzenia równania, co było widać na prezentacji. Poniżej animowana ilustracja tego faktu. Efekt ten został zarejestrowany podczas przenoszenia kursora tekstowego wewnątrz równania. Obserwuje się go także podczas klikania myszką odpowiedniego fragmentu równania. Te wewnętrzne bloki wyznaczają obszary, których dotyczyć będą wprowadzane zmiany i edycje.
  
  

  Prezentacja po konwersji. Naprowadź myszkę na ten tekst aby przeczytać uwagę.
  

  
  
  
  Na przykład, jeżeli zaznaczony jest blok zawierający wyrażenie f a kursor znajduje się po prawej stronie, to dopisanie ciągu „+2” dopisze go po wyrażeniu f, zatem dotychczasowy indeks górny tego wyrażenia znajdzie się teraz przy liczbie 2. Gdyby zaznaczony był blok indeksu górnego a kursor znajdował się po lewej stronie bloku, dopisany ciąg utworzyłby indeks o postaci +22.
• Zasady edytora równań Word powodują, że podczas wpisywania treści równania edytor wszystkie wyrażenia wprowadza pismem pochyłym. Pismem prostym wprowadzane są liczby, nazwy funkcji, „Normalny tekst” i wielkie litery alfabetu greckiego.
• Podczas edycji do opuszczenia wewnętrznego bloku wykorzystywany jest klawisz „strzałka w prawo” albo „strzałka w lewo” , natomiast klawisz spacji oprócz tworzenia dodatkowego odstępu, odgrywa specjalną rolę przy tworzeniu równania w postaci liniowej.
• W profesjonalnej postaci równania podczas edytowania nie zawsze można użyć klawiszy DELETE lub BACKSPACE do usuwania zbędnych komponentów. W szczególności nie można usunąć w ten sposób elementów będących integralną częścią struktury, np. nie można usunąć indeksu górnego lub dolnego, stopnia pierwiastka, licznika lub mianownika ułamka. Usunięcie takiego elementu przekształca go w symbol zastępczy, natomiast próba usunięcia symbolu zastępczego prowadzi do usunięcia całej struktury.

Tworzenie równań metodą zapisu liniowego.

Liniowy sposób wprowadzania równania pozwala tworzyć je szybciej, wymaga jednak poznania nowych zasad zapisu. Niektóre są dość proste, inne wymagają zapamiętania procedur i składni właściwej dla danej konstrukcji. Już na rys. 3 widać pewne charakterystyczne symbole włączane do treści równania, znak „^” symbolizujący indeks górny oraz znak „_” (podkreślnik) symbolizujący indeks dolny. Zapisy wprowadzone po tych znakach będą traktowane jak indeksy, odpowiednio: górny i dolny. Znacznikiem określającym koniec indeksu jest znak dowolnego operatora, gdy jednak nie jesteśmy pewni czy edytor rozpozna koniec takiego wyrażenia można nacisnąć spację. Oto kilka przykładów zapisu liniowego i odpowiadającej mu postaci profesjonalnej.

Ostatni przykład zawiera dwa niepokojące symbole, literę Θ i znak √. Na klawiaturze nie ma tych symboli, znajdują się natomiast na listach symboli dostępnych w równaniach. Zamiarem liniowej budowy równania nie jest jednak korzystanie z wybierania symboli z listy, chociaż nie jest to zakazane, ale wykorzystywanie klawiatury. Problem ten został rozwiązany poprzez wykorzystanie dodatkowej autokorekty, nazywaną autokorektą matematyczną. Działa ona analogicznie do znanej już autokorekty tekstowej. Po wpisaniu określonego ciągu znaków, ciąg ten zostanie zastąpiony odpowiednim symbolem matematycznym. Autokorekta matematyczna działa w obrębie bloku równania matematycznego. Można ją jednak także uaktywnić w obszarze zwykłego tekstu, dzięki czemu można umieszczać w zwykłym tekście symbole matematyczne. Należy jednak pamiętać, że w obszarze tekstu zwykła autokorekta ma pierwszeństwo przed autokorektą matematyczną.

Zamiana ciągu znaków na pojedynczy symbol następuje podczas pisania. Dlatego np. wpisanie kolejno znaku plus i minus zamieni je na jeden znak ±, natomiast wprowadzenie tych znaków w kolejności minus plus wstawi znak ∓. W analogiczny sposób przekształcane są inne operatory i symbole, np. wprowadzenie znaków „>=” wprowadzi do równania symbol ≥ a wpisanie „~=” wstawi znak ≅. Oprócz typowego układu dwóch symboli, które są zamieniane na jeden, istnieje cała lista wyrażeń tekstowych, których wprowadzenie wstawi odpowiedni symbol. Te wyrażenia zawsze zaczynają się od znaku „\” a po ich wpisaniu zastępowane są odpowiednim symbolem.

Dla widocznego powyżej symbolu pierwiastka wyrażenie to należy wpisać następująco, „\sqrt”, aby wstawić grecką literę teta należy wpisać: „\Theta”. W przypadku liter greckich autokorekta rozpoznaje ich angielskie nazewnictwo, przy czym jeśli pierwszą literą tej nazwy będzie wielka litera (jak w przykładzie powyżej) zostanie ona zamieniona na wielka literę alfabetu greckiego, jeśli mała – na małą literę tego alfabetu. Przy okazji: wielkie litery alfabetu greckiego wstawiane są pismem prostym a małe – pochyłym.

W analogiczny sposób wprowadzić można do równania wpisy skryptowe, fraktury czy litery z podwójną linią. W tym wypadku ostatnia litera wyrażenia decyduje o postaci wynikowej. Zatem zapis „\frakturC” da wielkie C a „\frakturc” – małe. Dla pozostałych dwóch wymienionych symboli fraza początkowa wygląda tak: „\script” dla liter skryptowych i „\double” dla liter o podwójnej linii.

Zazwyczaj po wprowadzeniu ciągu rozpoznawanego przez autokorektę matematyczną następny wprowadzony znak powoduje przekształcenie wyrażenia do oczekiwanej postaci. Ale nie zawsze tak musi się wydarzyć, np. wpisanie ciagu „\scriptOa” nie spowoduje wstawienia skryptowej litery „O” z następującą po niej literą „a” gdyż dla autokorekty ten ciąg jest nierozpoznawalny. Aby jednak zrealizować taki zamysł, należy właściwe wyrażenie zakończyć spacją. Wpisanie spacji na końcu właściwego wyrażenia zawsze spowoduje przekształcenie go na odpowiadający mu symbol, bez wstawiania dodatkowego odstępu. Przekształcenie nastąpi także, gdy następnym znakiem po wyrażeniu będzie znak nawiasu, kropki, podkreślnika, daszka, operatora relacji itp. Wyjaśniając to zagadnienie do końca, wyrażenie rozpoznane przez autokorektę matematyczną jest zastępowane symbolem pojawiającym się w równaniu. Równania nie można przekształcić w przeciwną stronę tak aby wstawione w nim symbole zostały ponownie pokazane jako wpisane wyrażenia.

Dlatego aby w przykładowym wzorze wpisać argumenty funkcji sinus należy wprowadzić ciąg „\Theta_o”. Mówiąc o autokorekcie matematycznej wspomniałem, że może ona także dotyczyć zwykłego tekstu znajdującego się poza obszarem matematycznym. Należy jednak pamiętać, że dotyczy to tylko zamiany na symbol, ewentualny znak daszka czy podkreślnika nie spowoduje uzupełnienia symbolu o odpowiedni indeks. Korzystając z linearnego konstruowania równań musimy też pamiętać o stosowaniu nawiasów dla wyróżnienia segmentów równania związanych z danym symbolem. W poniższej prezentacji pokażę jak powstaje znane już z wcześniejszej prezentacji równanie, tym razem jednak z wykorzystaniem wyłącznie klawiatury.

Prezentacja po konwersji. Naprowadź myszkę na ten tekst aby przeczytać uwagę.

Ostateczna postać równania jest nieco inna niż ta wcześniejsza, ale matematycznie oznacza to samo. Dlaczego tak się stało? Dlatego, że po pierwsze wpisałem znak plusa zamiast minusa a po drugie po wpisaniu wartości 81 powinienem postawić spację i dopiero wtedy napisać ciąg dalszy tego wyrażenia, w tym przypadku literę „N”. To był jak widać niezamierzony przykład na ukazanie znaczenia wstawianych lub pominiętych znaków.

Kiedy gotowe równanie widziane w postaci profesjonalnej przekształcimy w postać liniową, może się okazać, że są w tej postaci znaki, jakich nie wprowadzaliśmy. Wynika to z tego, że edytor przekształcając równanie stosuje sformalizowaną postać takiego równania i uzupełnia je o pominięte, lecz potrzebne z formalnego punktu widzenia, symbole.

Aby poznać wszystkie dopuszczalne wyrażenia konwertowane na symbole matematyczne należy przejść do opcji programu Word i wybrać w nich sekcję „Sprawdzanie” a w otwartym po prawej stronie oknie ustawień tej sekcji, kliknąć przycisk „Opcje autokorekty…”. W otwartym okienku autokorekty można przejść do zakładki „Autokorekta matematyczna” i zapoznać się ze wszystkimi wyrażeniami będącymi zamiennikami symboli, oraz ustalić czy ta autokorekta ma także działać w obszarze zwykłego tekstu.

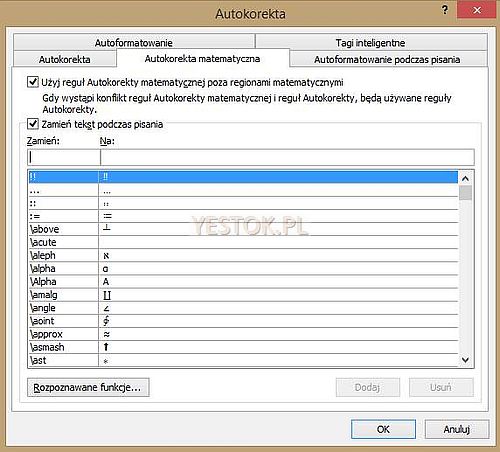
Widoczny na ilustracji przycisk „Rozpoznawane funkcje…” otworzy kolejne okno, w którym wymienione są wszystkie funkcje rozpoznawane przez edytor równań. Dzięki tej liście, podczas tworzenia równania edytor, rozpoznając nazwę funkcji, wprowadza ją do równania pismem prostym. Okno to pozwala także na uzupełnienie listy o nowe nazwy.

Oprócz poznanych już wyrażeń warto także poznać ich składnie. Wpisanie poznanego już wyrażenia „\sqrt” w postaci „\sqrt(n&b) wstawi do równania pierwiastek n-tego stopnia z wartości b, pominięcie elementu „n&” oznacza, że chodzi o pierwiastek kwadratowy. Przy okazji dodam, że dla pierwiastka trzeciego stopnia wprowadzono oddzielne wyrażenie „\cbrt”, a dla czwartego – „\qdrt”.

Więcej informacji na temat równania w formacie liniowym znajduje się w pomocy programu Word. Wyekstrahowałem ten fragment do oddzielnego dokumentu w standardzie Worda i można go pobrać klikając link obok: liniowe_word.docx . W tym dokumencie mowa jest także o innym opracowaniu szczegółowo opisującym te zasady, dokumencie pt. „Unicode Nearly Plain-Text Encoding of Mathematics”. Ten dokument w formacie PDF, którego autorem jest Murray Sargent z Microsoft, także można pobrać, klikając link: utn28-plaintextmath-v2.pdf. Opracowanie jest w języku angielskim.

Jeżeli chcecie Państwo pobrać plik, pamiętacie, że za taką możliwość odpowiada kliknięcie odnośnika (łącza) prawym przyciskiem myszki i wybranie z wyświetlonego menu pozycji w rodzaju „Zapisz element docelowy jako...” lub „Zapisz link jako...”. Kliknięcie lewym przyciskiem może spowodować inne działania niż pobieranie, gdyż przeglądarka może próbować bezpośredniego odczytania pliku. W szczególności, większość przeglądarek ma obecnie włączoną możliwość bezpośredniego odczytywania plików PDF.

Równania przedstawione w postaci liniowej łatwo jest edytować, gdyż edytor nie wyróżnia w nich wyodrębnionych struktur i każdy znak i symbol można potraktować indywidualnie. Inaczej jest, jeśli edycja równania ma być zrealizowana w postaci profesjonalnej. W niej wyróżnia się wewnętrzne bloki związane z różnego rodzaju strukturami. Wspomniałem już o tym wcześniej, że w pewnych sytuacjach nie można usunąć zbędnego elementu, gdyż taka próba spowoduje, że najpierw pojawi się symbol zastępczy. Próba usunięcia symbolu zastępczego prowadzi do usuwania całej struktury. W edytorze równań dla postaci profesjonalnej rozwiązano to wykorzystując możliwości menu kontekstowego. Przypomnę, że menu kontekstowe wywoływane jest kliknięciem prawym przyciskiem myszy na interesującym nas obiekcie.

Menu kontekstowe, są w tym wypadku rzeczywiście kontekstowe, bo są odmienne dla różnych struktur znajdujących się w równaniu. Nie będę w stanie o każdym z nich opowiedzieć, ale chcę dać pogląd na jego funkcjonowanie, na przykładzie znanego już równania. Użytkownicy tworzący różne rodzaje równań powinni samodzielnie sprawdzić, jakie możliwości udostępnia im menu kontekstowe danego elementu równania.

Podstawowe menu kontekstowe dostępne jest, gdy zaznaczone jest całe równanie albo, gdy w miejscu kliknięcia, edytor nie może zaproponować innych możliwości. To podstawowe menu przedstawiam poniżej.

Jak widać menu zawiera standardowe działania „Wytnij”, „Kopiuj” i „Wklej”, następnie znane już z umiejscowienia w innych menu: „Profesjonalny”, „Liniowy” i „Zapisz jako nowe równanie…”. Dodatkowe dwie pozycje „Czcionka…” i „Akapit” otwierają okna dialogowe znane z normalnej edycji tekstu, jednak ich działanie jest ograniczone i nie wszystkie opcje dadzą się użyć.

Gdy jednak kliknąć prawym przyciskiem myszki tak, aby zaznaczony został blok indeksu dolnego, menu kontekstowe zmieni się i wygląda teraz tak:

W tym menu pojawiły się trzy nowe możliwości. Można w ogóle usunąć indeks (a tego nie można akurat zrealizować klawiszem DELETE lub BACKSPACE), albo można powiększyć lub zmniejszyć rozmiar argumentu. Zwiększanie lub zmniejszanie argumentu można powtarzać kilkukrotnie, aż do zniknięcia tej pozycji z menu, co zasygnalizuje osiągnięcie granicznej wartości.

Kliknięcie zaznaczające jednocześnie blok podpierwiastkowy generuje inne menu:

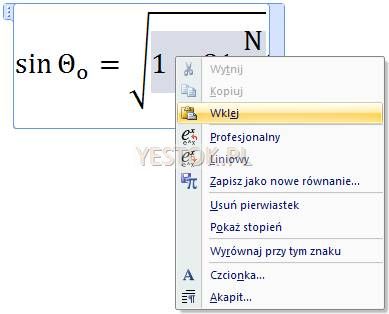
W tym menu edytor umożliwia usunięcie znaku pierwiastka albo pokazanie jego stopnia. Usunięcie znaku pierwiastka z równania pozostawi całe wyrażenie podpierwiastkowe. Pokazanie stopnia – doda symbol zastępczy, w którym można wpisać stopień pierwiastka. Z kolei w menu kontekstowym stopnia pierwiastka, pojawi się możliwość zwiększenia lub zmniejszenia argumentu. Jeśli argument zostanie usunięty klawiszem DELETE lub BACKSPACE to menu kontekstowe widocznego wówczas symbolu zastępczego zawierać będzie możliwości ukrycia stopnia pierwiastka.

Kolejny przykład, jaki chcę przedstawić to kliknięcie w ułamek. To menu kontekstowe przedstawia następna ilustracja, na której widać możliwości zmiany postaci ułamka.

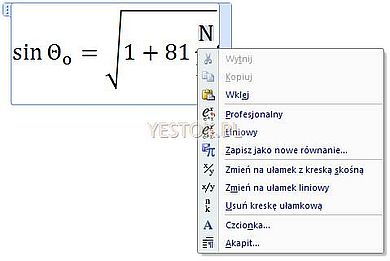
Menu kontekstowe pozwala modyfikować równanie w zakresie zmian możliwych dla danej konstrukcji równania, dlatego autorzy powinni sami rozpoznać te możliwości. Gdzieś na forach znalazłem pytanie jak utworzyć macierz większą niż 3×3, bo struktura umożliwia wstawienie tylko takiej. Otóż menu kontekstowe macierzy umożliwia wstawienia albo usunięcie wiersza albo kolumny, a nawet pozwala ustalić odstępy międzyelementowe. Pytający jak widać nic nie wiedział o menu kontekstowym. Jednak tak naprawdę najbardziej upraszcza ten problem wykorzystanie liniowej postaci macierzy. Wpisanie np. ciągu „\matrix(@@@@&&&)” utworzy automatycznie macierz 5×4 wypełnioną symbolami zastępczymi.

Jak duże równanie można utworzyć?

Dokumentacja nic nie mówi o ograniczeniach. Równanie bardzo długie zostanie automatycznie przełamane i kontynuowane w następnym wierszu, podobnie jak przy łamaniu wiersza w akapicie. Jednak to edytor decyduje o miejscu podziału. Można również samodzielnie wskazać miejsce, w którym ma nastąpić przełamanie równania o ile to miejsce może być punktem podziału. Równanie może być przełamywane wielokrotnie tworząc wielowierszowe wyrażenie. Po kliknięciu prawym przyciskiem myszki w wybraną część równania pojawi się menu kontekstowe dla tego miejsca. Jako przykładu użyję znanego już równania, w którym kliknąłem prawym przyciskiem myszki przed znakiem równości.

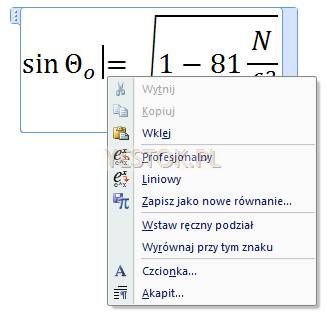
Jeżeli miejsce, w którym kliknięto prawym przyciskiem myszki może być punktem podziału, w menu kontekstowym pojawi się polecenie „Wstaw ręczny podział”. Wstawienie podziału ręcznego przekształci równanie do postaci takiej jak poniżej:

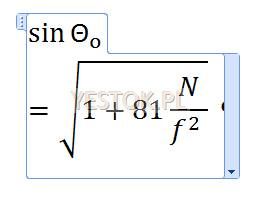
Jest to nadal jednolity obszar matematyczny. Wywołanie menu kontekstowego na granicy podziału obszaru umożliwia jego cofnięcie po wybraniu polecenia „Usuń ręczny podział”.

W tym miejscu pora już na omówienie jeszcze jednego okna dialogowego, pozwalającego ustalić ogólne opcje dotyczące równań. Okno to otwiera się po kliknięciu w przycisk otwierania okna znajdujący się na prawo od nazwy grupy „Narzędzia” zakładki „Projektowanie”. To okno wygląda następująco:

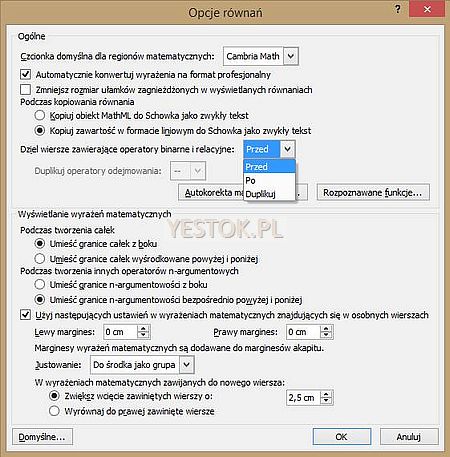
Okno składa się z dwóch części: „Ogólne” i „Wyświetlanie wyrażeń matematycznych”. Same parametry są na tyle szczegółowo opisane, że znaczenie tych opcji jest zrozumiałe. Tutaj wspomnę tylko, że lista dostępnych czcionek składa się tylko z czcionki Cambria Math. Ilustracja przedstawia stan przed wyborem sposobu umieszczania operatorów w wierszach dzielonych. „Przed” oznacza, że operator pojawi się, jako pierwszy znak w wierszu kontynuacji równania, „Po”, że operator będzie ostatnim znakiem wiersza natomiast „Duplikuj” oznacza, że operator zostanie powtórzony i znajdzie się zarówno na końcu wiersza dzielonego jak i na początku wiersza kontynuacji. Jeżeli operator będzie duplikowany to można dodatkowo wybrać, w jaki sposób ma być duplikowany operator odejmowania. Do wyboru są: dwa minusy, plus na końcu i minus na początku lub minus na końcu i plus na początku.

Dwa przyciski: „Autokorekta matematyczna…” i „Rozpoznawane funkcje…” są tymi samymi przyciskami, o jakich napisałem przy omawianiu „Opcji programu Word”.

Opcje równań zawijanych do nowego wiersza dotyczą tylko tych równań, w których zawinięcie zostało wymuszone przez edytor równań. Nie dotyczą równań, w których to zawinięcie zostało wymuszone.

Ustalone opcje równań będą dotyczyły wszystkich równań tworzonych w dokumencie. Przycisk „Domyślne…”, znajdujący się w lewym dolnym rogu, pozwala ustalone opcje równań przypisać do szablonu Normal.dotx, co oznacza, że będą one obowiązywały w każdym nowotworzonym dokumencie.

Bardzo duże równania można podzielić w jeszcze jeden sposób. Mianowicie, podczas pisania równania nacisnąć skrót klawiaturowy SHIFT+ENTER, czyli wprowadzić znak nazywany „miękkim enterem”. W zwykłym akapicie to działanie powoduje zakończenie wiersza i rozpoczęcie nowego, bez zakończenia akapitu. W obszarze matematycznym powoduje zakończenie jednego obszaru matematycznego i otwarcie następnego, znajdującego się w kolejnej linii. Postępując w ten sposób można utworzyć wiele linii jednego równania, albo, – co narzuca się samo z siebie – utworzyć wiele równań, każde w oddzielnej linii. Dopiero w takiej sytuacji można zobaczyć, na czym polega różnica między justyfikacją „Do środka” a „Do środka jako grupa”. Pokażę to na przykładzie trzech równań:

Najwyżej na ilustracji znajduje się układ wyrównany „Do lewej”. Poniżej wyrównany „Do prawej”. Trzeci układ wyrównywany jest „Do środka” a więc każde równanie jest wyrównane indywidualnie do środka strony. Najniższy układ równań wyrównany jest „Do środka jako grupa”, w takiej sytuacji do środka wyrównane jest najdłuższe z równań a pozostałe wyrównane są do pierwszego znaku tego najdłuższego równania.

Układy równań i ich wewnętrzne wyrównywanie

Bardzo często autorzy chcą umieścić układ równań w taki sposób, aby były one wzajemnie wyrównane względem wybranego znaku. Często tym znakiem jest symbol „=”. Dlatego po zaznaczeniu obszarów zawierających te równania (wystarczy kliknąć wewnątrz układu trzykrotnie myszką) i kliknięciu prawym przyciskiem myszki, w menu kontekstowym pojawi się pozycja „Wyrównaj do =”, tak jak na ilustracji poniżej.

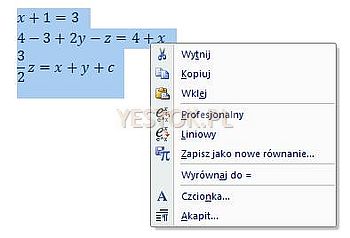
Wybór tej opcji spowoduje, że obszary matematyczne zostaną wyrównane względem siebie na znaku „=” a efekt justyfikacji takiego układu przedstawiał będzie się następująco:

Na górze ilustracji równania wyrównane są „Do lewej” w taki sposób, aby znak „=” znajdował się w jednej linii we wszystkich równaniach. Poniżej zadysponowane wyrównanie „Do prawej” pokazuje nieoczekiwane i błędne działanie Worda (tak to widzę w 2007, nie wiem jak jest w nowszych wersjach). Tylko pierwsze z równań zostało wyrównane do prawej strony, pozostałe znajdują się po stronie lewej. Justyfikacja „Do środka” ignoruje jak widać wyrównywanie względem znaków równości, no i w końcu „Do środka jako grupa” wyrównuje obszary względem znaku „=” a środek wyznaczony jest z uwzględnieniem położenia znaków leżących najbardziej na lewo i najbardziej na prawo w tych obszarach.

Po włączeniu opcji „Pokaz wszystko” (CTRL+*, gwiazdka z alfanumerycznej części klawiatury) w obszarze matematycznym można zobaczyć tylko trzy dotychczas ukrywane symbole. Znak końca akapitu, znak „miękkiego entera” i znak pozycji wyrównywania. Zauważmy, że nie są ujawniane spacje.

Pionowe linie przy znaku „=” symbolizują pozycję znaku, przy którym ma nastąpić wyrównanie. Autor może wybrać inne miejsce w równaniu, które będzie pozycją wyrównywania albo usunąć pozycję wyrównywania. W menu kontekstowym wywołanym w obszarze matematycznym, może pojawić się pozycja „Wyrównaj przy tym znaku” (taką pozycje w menu widać na rys. 15.) albo, jeśli wywołano je na znaku wyrównywania – „Usuń punkt wyrównania”. Pierwsze z poleceń ustawi punkt wyrównania, i jeśli w kolejnym obszarze zostanie także ustawiony punkt wyrównania, to oba te punkty pokryją się i równania będą wyrównane względem tego miejsca. Drugie polecenie usunie punkt wyrównania. Aby wskazać inny niż aktualnie ustawiony punkt wyrównania, należy wybrać właściwe miejsce i w menu kontekstowym przywołać „Wyrównaj przy tym znaku”. Ponieważ w obszarze może wystąpić tylko jeden punkt wyrównania, dotychczasowy zostanie usunięty. Wyrównywanie dotyczy tylko układu kolejnych obszarów matematycznych rozdzielonych znakami „miękkiego entera”.

Jeżeli utworzono kilka równań, jedno pod drugim, każde kończąc zwykłym naciśnięciem klawisza ENTER, czyli równania znajdują się w kilku kolejnych akapitach, to można te akapity zaznaczyć a w menu kontekstowym tych zaznaczonych akapitów także pojawi się pozycja „Wyrównaj do =”. Word rozpozna, że kolejne akapity zawierają tylko obszary matematyczne. Wybór wyrównania spowoduje, że te niezależne obszary zostaną połączone w jeden akapit, w którym każdy obszar zakończony będzie znakiem „miękkiego entera” a cały układ będzie wyrównany do znaku „=”.

Sposoby budowania układów równań.

Skoro wspomniałem o układzie równań to oprócz wspomnianego sposobu, czyli utworzenia tego układu z kilku równań wpisanych do kolejnych wierszy akapitu, można też wykorzystać struktury edytora. Jako naturalna narzuca się możliwość wykorzystania struktury macierzy jednokolumnowej. Każdy symbol zastępczy takiej struktury można „wypełnić” równaniem. Właściwości menu kontekstowego dotyczącego kolumny macierzy pozwolą wybrać rodzaj wyrównania elementów kolumny. Są trzy takie możliwości: „Do lewej”, „Do środka” i „Do prawej”. Nie ma tu możliwości wyrównania równań względem konkretnego znaku. Dla edytora macierz jest jednym obszarem matematycznym a jak wspomniałem w takim obszarze może wystąpić tylko jeden znak wyrównania. Rozwiązaniem problemu wyrównania jest zastosowanie macierzy dwukolumnowej. Elementy kolumny pierwszej (lewej), zawierające pierwszą część równania, należy wyrównać „Do prawej” natomiast elementy kolumny drugiej (prawej), zawierającej dokończenie równania, wyrównać „Do lewej”. Ustalając odstęp miedzy kolumnami, (co także jest możliwe z poziomu menu kontekstowego) można doprowadzić do właściwej prezentacji układu równań. Taki szablon układu równań, zawierający tylko symbole zastępcze, można zapisać, jako nowe równanie i wykorzystywać w swoich opracowaniach. Menu kontekstowe pozwoli dodawać kolejne wiersze do takiej konstrukcji a więc zwiększać liczbę równań albo usuwać zbędne wiersze. Strukturę macierzy można utworzyć wykorzystując liniowy sposób jej utworzenia. Wyrażeniem tworzącym taką strukturę jest „\matrix” z podaną w nawiasach macierzą. Elementy macierzy oddzielane są odstępami. W treści zapisu mogą wystąpić dwa znaki specjalne determinujące konstrukcję układu. Znak „&” sygnalizujący opuszczenie jednego wyrazu macierzy i znak „@” informujący o początku kolejnego wiersza. Przed tymi znakami ani po nich nie stawia się odstępu. Przykład tego zapisu pojawił się kilka akapitów wcześniej. Wpisanie ciągu „\matrix() „ utworzy macierz złożoną z jednego elementu, zastąpionego symbolem zastępczym. Wpisanie: „\matrix(1&@&1)” utworzy macierz jednostkową 2×2. Taką samą macierz utworzy wpis „\matrix(1 0@0 1), jednak w tym przypadku w macierzy znajdą się wszystkie elementy.

Szablony konstrukcyjne znajdujące się w strukturach pozwalają na zbudowanie układu równań, po wybraniu pierwszego szablonu w ostatnim wierszu rozwiniętej listy struktury „Nawias”. Tyle, że strukturę tę należy odpowiednio zmodyfikować. Istnieje jednak specjalny symbol informujący edytor równań o tworzeniu układu równań. Autokorekta matematyczna rozpoznaje ten symbol po wpisaniu ciągu „\eqarray”. W nawiasach występujących w wyrażeniu należy zakodować układ równań. Wykorzystuje się tu także dwa wspomniane już znaki kodujące: „&” – który w tym wyrażeniu ma inne znaczenie i wskazuje miejsce wyrównania kolejnego równania i „@” – oznaczający początek następnego równania w układzie. Znak „&” nie musi być stosowany, jeżeli nie jest wymagane wskazanie punktu wyrównywania. Ten znacznik wyrównywania wpływa tylko na równania znajdujące się w zakresie działania wyrażenia „eqarray”. Znaki wyrównania są widoczne w podglądzie przy włączonej opcji: „Pokaż wszystko”, ale nie mogą zostać usunięte, gdyż stanowią treść wyrażenia „eqarray”. W liniowej postaci równania pokazywane są już jako znaki „&”.

W takim obszarze matematycznym można wstawić niezależny znak wyrównywania korzystając z menu kontekstowego, lecz będzie on oddziaływał z podobnym znakiem w sąsiednim, niezależnym obszarze. Za chwilę na ilustracji będzie to można zobaczyć.

Piszę o tych sposobach tworzenia układów równań, dlatego że często autorzy chcą taki układ równań objąć klamrą jednostronną. Np. tak, jak to przedstawia rys. 22. Efekt nawiasu lub klamry obejmujący kilka równań można uzyskać w pojedynczym obszarze matematycznym a taki obszar tworzy zarówno macierz jak i układ równań.

Przedstawiony na powyższym rysunku układ dwóch obszarów matematycznych został wyrównany względem zaznaczonych na ilustracji miejsc. Miejsca te zarówno w górnym obszarze jak i w dolnym zostały ustalone przez wykorzystanie menu kontekstowego i można je dowolnie zmienić. Widoczne w górnym obszarze kolejne symbole wyrównywania (przy znaku równości) są wynikiem wstawienia do wyrażenia „eqarray” znaków „&” i aby te miejsca zmienić należałoby przeredagować to wyrażenie, przekształcając je najpierw w postać liniową. Formalny zapis liniowy górnego obszaru ma postać: „{\eqarray(x+1&=2@1+2+3+y&=z@x+y&=2@3/x&=6)\close”. Wyrażenie „\close”, widoczne na końcu zapisu, wstawia nieujawniany symbol nawiasu zamykającego, w przypadku tego konkretnego równania – klamrowego. Jeśli autor nie wprowadzi tego wyrażenia, edytor równań uzna, że równanie nie jest kompletne i nie będzie go mógł przekształcić do postaci profesjonalnej. Podczas „ręcznego” tworzenia równania trzeba koniecznie pamiętać o tym, że każdy nawias pojawiający się w równaniu musi mieć swój komplementarny odpowiednik. Jeśli ten odpowiednik nie ma być ujawniany – na rys. 22. nie ma klamrowego nawiasu zamykającego – należy go zasygnalizować symbolem zastępczym „\close”. Odpowiednikiem nieujawnianego nawiasu otwierającego jest wyrażenie „\open”, które edytor równań przekształci w symbol zastępczy ukrytego nawiasu otwierającego. Wyrażenia te są zamiennikami nawiasów każdego typu.

Zapisywanie równania.

Gotowy obszar matematyczny lub spójny układ takich obszarów może zostać zapisany i wielokrotnie wykorzystywany. Zapis nie tworzy jednak odrębnego pliku, ale twór, który nazywany jest blokiem konstrukcyjnym i zapisywany jest w bibliotece takich bloków. Biblioteka bloków konstrukcyjnych nosi nazwę „Building Blocks.dotx” i jest otwierana przy każdym uruchomieniu Worda, umożliwiając autorowi na korzystanie z jej zasobów. Po wybraniu polecenia „Zapisz jako nowe równanie…” otwarte zostanie okienko dialogowe umożliwiające sprecyzowanie niezbędnych danych dotyczących tego bloku konstrukcyjnego. Na rysunku poniżej przedstawiam obszar matematyczny, dla którego taki blok konstrukcyjny jest tworzony i związane z nim okno dialogowe.

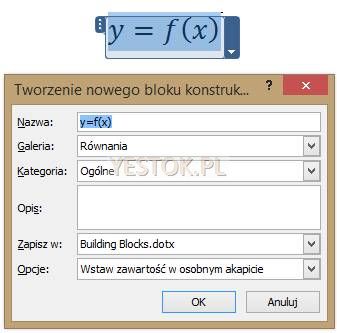
Pierwsze pole – „Nazwa” – zawiera treść równania w postaci liniowej, funkcja tworzenia bloku robi to automatycznie. W tym polu można i właściwie należy wpisać własną nazwę przypisaną do tworzonej konstrukcji, np. „Funkcja jednej zmiennej”. Poprzez tę nazwę będzie można odnaleźć blok i wstawić go do opracowania.

Pole „Galeria” pozwala wskazać, do jakiego zestawu bloków konstrukcyjnych zostanie dodany ten konkretnie definiowany.

Pole „Kategoria” początkowo ma trzy możliwości wyboru: „Ogólne”, „Wbudowane” i „Utwórz nową kategorię…”. Wybór pozycji „Wbudowane” oznacza, że dodany blok konstrukcyjny pojawi się pod podaną nazwą na rozwijalnej liście równań pokazanych na rys. 5. Utworzenie nowej kategorii pozwoli zapisać bloki konstrukcyjne w wyodrębnionych zestawach, np. Fizyka, Algebra, Geometria, itp.

Pole „Opis” przeznaczone jest na krótki opis bloku zwłaszcza, gdy znajduje się w nim wiele równań i trzeba dokładniej wyjaśnić ich sens. Jeśli kategorią równania będzie „Wbudowane”, opis ten pojawi się w „dymku” podpowiedzi, pojawiającym się po nakierowaniu wskaźnika myszki na równanie na rozwiniętej liście równań wbudowanych.

Pole „Zapisz w:” pozwala wskazać inne miejsce zapisu niż plik „Building Blocks.dotx”. Takim innym miejscem może być szablon. Przy omawianiu tego zagadnienia przyjmuję, że zapis następuje do bloku konstrukcyjnego.

Ostatnie pole: „Opcje” pozwala ustalić sposób wstawiania bloku konstrukcyjnego do dokumentu. Do wyboru są trzy możliwości, widoczna na ilustracji i proponowana: „Wstaw zawartość w osobnym akapicie” oraz „Wstaw tylko zawartość” i „Wstaw zawartość na osobnej stronie”. Opis opcji jednoznacznie wskazuje na charakter akcji związanej z wstawianiem bloku.

Po zatwierdzeniu okna dialogowego blok zostanie dodany do biblioteki, ale uwaga(!) biblioteka zostanie zaktualizowana dopiero przy zakończeniu pracy z programem Word. Dopiero wtedy pojawi się pytanie czy biblioteka ma zostać zaktualizowana.

Jak wstawić równanie zapisane w bibliotece bloków konstrukcyjnych? Jeśli równanie zostało zapisane w kategorii „Wbudowane” znajdzie się w rozwijanej liście równań wbudowanych. Jeśli nie, należy w zakładce „Wstawianie”, w grupie „Tekst” rozwinąć listę opcji polecenia „Szybkie części…” i wywołać pozycję „Organizator bloków konstrukcyjnych…”. W otwartym oknie organizatora odnaleźć właściwą galerię, kategorię i nazwę bloku, zaznaczyć go i nacisnąć przycisk „Wstaw”.

Numerowanie równań.

Ostatnim tematem, o jakim chcę napisać jest numerowanie równań. W pracach związanych z naukami ścisłymi i technicznymi równania są numerowane po to, by w łatwy sposób odwoływać się do nich w opracowaniu.

Już na początku wspomniałem, że numerowanie równań jest właściwie piętą achillesową tego systemu budowania równań. Zaproponuję tu rozwiązanie będące, co prawda protezą, ale dobrze spełniającą swoje zadanie. Czytelnicy szukający w sieci rozwiązania tego problemu znajdą sporo stron opisujących rozwiązanie problemu. Wszystkie metody opierają się o utworzenie jednowierszowej i trzykolumnowej tabelki, w której centralna komórka przeznaczona jest na równanie, zaś lewa albo prawa – na numer kolejny równania. Jednym z takich miejsc opisujących ten problem jest np. http://www.dobreprogramy.pl/iluzion/Automatyczna-numeracja-wzorow,18801.html.

Poza samym numerowaniem równań chciałem osiągnąć jeszcze taki efekt by odwołanie się do numeru równania było możliwe przy użyciu odsyłaczy. Znalazłem własne rozwiązanie, ale Andreas Rejbrand, którego serwis Internetowy wymieniłem już na początku opracowania znalazł znakomity sposób. Przedstawię go teraz a w dalszej części uzupełnię o moją propozycję osiągnięcia możliwości odwoływania się do numeru równania w pewnych specyficznych sytuacjach.

Metoda także opiera się o wykorzystanie tabelki, co wynika ze wspomnianego już przeze mnie faktu, że umieszczenie jakiegokolwiek znaku w wierszu zawierającym obszar matematyczny, przekształca ten obszar i znajdująca się w nim konstrukcję na styl „Wbudowany”.

1. Utwórz tabelkę 1×3.
2. Korzystając z okna dialogowego „Właściwości tabeli” i zakładki „Tabela” ustal jej szerokość na 100%. (Procentowe ustalenie tej wartości sprawi, że będzie zawsze dopasowana do szerokości strony). Takie samo działanie spowoduje wyłączenie na tej karcie opcji: ”Preferowana szerokość”. By formalnie tabela była prawidłowo skonfigurowana należałoby w tej zakładce ustawić jeszcze „Wyrównanie” na: „Wyśrodkuj”, „Zawijanie tekstu” na: „Brak” i „Wcięcie z lewej” na wartość 0.
3. W tym samym oknie dialogowym „Właściwości tabeli”, ale w zakładce „Kolumna”, określ szerokość kolumn tabeli odpowiednio na 10%, 80% i 10%.
4. Wykorzystując we wstążce narzędziowej grupę „Wyrównywanie”, w zakładce „Układ” „Narzędzi tabel”, ustaw wyrównanie zawartości komórki centralnej na „Wyrównaj do środka w poziomie”.
5. Ustal wyrównywanie prawej komórki tabeli na „Wyrównaj do prawej środkowej”.
6. Wyłącz obramowania tabeli wykorzystując zakładkę „Projektowanie” w narzędziach tabel.
7. Zaznacz całą tabelę i ustaw odstęp „Po akapicie” na 10 pkt lub na taką wartość, jakiej w swoim tekście używasz do oddzielania akapitów. Możesz to zrobić w zakładce „Układ strony” w grupie „Akapit” sekcja „Odstępy” albo w zakładce „Narzędzia główne” wybierając przycisk otwierający okno dialogowe grupy „Akapit”.
8. Wstaw puste równanie do środkowej komórki.
9. Zakończenie pracy na tym etapie utworzy tabelę przygotowaną do ręcznego wprowadzania numerów równań. Jeśli taki sposób jest wystarczający przejdź do punktu 12.
10. Do automatycznego numerowania równań wykorzystam metodę opartą o pola programu Word. Jest to proces podobny do podpisywania tabel i rysunków. Wśród pól programu Word występuje pole o nazwie SEQ, z przypisanym identyfikatorem pola. Wstawienie tego pola do dokumentu umieszcza w nim numer kolejny wystąpienia identyfikatora. Pola o różnych identyfikatorach numerowane są niezależnie.
11. Do prawej kolumny tabelki wstaw nawiasy (). Umieść kursor tekstowy między tymi nawiasami i naciśnij na klawiaturze CTRL+F9. Wpisz w ujawnionym obszarze sekwencję: „SEQ<spacja>Równanie” i naciśnij F9 Zapis powinien zostać przekształcony do postaci (1). Każde pojawienie się pola SEQ z identyfikatorem „Równanie” umieści w dokumencie liczbę odpowiadającą kolejnemu wystąpieniu tego pola.
12. Zaznacz całą tabelę, a następnie naciśnij na klawiaturze ALT+F3. Zostanie rozpoczęta procedura tworzenia bloku konstrukcyjnego.
13. W polu „Nazwa” przypisz blokowi jakąś nazwę np. #nrr. W polu „Galeria” wybierz pozycję „Autotekst” a kategorię „Ogólne”. W polu „Zapisz w:” wybierz plik „Normal.dotm” a w „Opcjach” wskaż „Wstaw tylko zawartość”. Naciśnij OK.

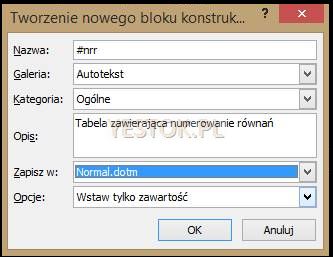
Blok konstrukcyjny został zapisany. Teraz wystarczy wpisać w wybranym miejscu opracowania nazwę przypisaną do właśnie utworzonego bloku konstrukcyjnego, w prezentowanym przykładzie #nrr i nacisnąć F3 a cała konstrukcja zostanie wstawiona do dokumentu.

Przypominam, że Word nie realizuje automatycznej aktualizacji pól. Jeśli tabelki z równaniami były dodawane w przypadkowej kolejności albo zmieniano ich kolejność podczas redagowania dokumentu, lub usunięto niektóre z nich należy zażądać aktualizacji wszystkich pól. Najlepiej zrobić to zaznaczając cały dokument (CTRL+a) a następnie nacisnąć klawisz F9.

Pole SEQ może zawierać dodatkowe przełączniki. Jednym z nich jest przełącznik „\s”, w którym po literze „s” występuje cyfra z zakresu od 1 do 9. Umieszczenie takiego przełącznika spowoduje, że numeracja identyfikatora będzie rozpoczynała się od początku w każdej części dokumentu rozpoczętej stylem o poziomie wskazanym przez cyfrę. Zapis „\s1” oznacza, że w każdym rozdziale rozpoczętym stylem o pierwszym poziomie konspektu (np. Nagłówek 1) numeracja równań rozpocznie się od nowa.

Jeśli więc autor opracowania tworzy strukturę konspektową swej pracy, to może ten fakt wykorzystać do wprowadzenia odrębnej numeracji równań w każdej części opracowania i wówczas w punkcie 11. powyższej procedury należałoby wprowadzić treść: „SEQ <spacja>Równanie<spacja>\s1”

W samym opracowaniu pojawia się potrzeba odwoływania się w jego treści do wybranych równań. Takie odwołania realizowane są przez odsyłacze. O problematyce wstawiania odsyłaczy napisałem oddzielne opracowanie pt. „Zakładki, hiperłącza i odsyłacze”. Andreas Rejbrand proponuje wykorzystanie w tym celu zakładek. Numerom równań, które zechcemy przywoływać w pracy, możemy przypisać zakładkę, nadając jej przyjazną nazwę. Dzięki temu łatwo wskażemy właściwe równanie. W obszernym opracowaniu, w którym występuje wiele równań a równania te mogą ciągle jeszcze zmieniać swą numerację, autorowi trudno jest zapamiętać, pod jakim numerem kryją się równania ważne dla późniejszego odwołania. Użycie zakładki upraszcza ten problem. W zależności od przyjętego sposobu odwoływania się do równań, zakładką można określić wyłącznie numer równania, lub numer wraz z otaczającymi go nawiasami.

Jeśli np. numerowi równania (12) przypisano zakładkę o nazwie „Bernoulli” to wykorzystując tę zakładkę można utworzyć odwołania, które w tekście mogą wyglądać następująco:

Jedno z podstawowych równań hydrodynamiki płynów idealnych przedstawia równanie (12) na stronie 44…

W tym przykładzie zarówno napis (12) jak i liczba 44 zostały wstawione przez odpowiednie odwołanie się do zakładki „Bernoulli”.

Przy takim wykorzystaniu zakładek przypisać je należy tylko tym równaniom, na które rzeczywiście będziemy się powoływać bezpośrednio (przytaczając ich numer) lub pośrednio (podając np. numer strony, na której się znajdują).

Chcę dodatkowo przedstawić jeszcze jeden sposób odwoływania się do numerów równań. Zanim poznałem rozwiązanie zaproponowane przez A. Rejbranda stosowałem własną, „słabszą” wersję tej metody. Dotyczy ona sytuacji, gdy równań przytaczanych w opracowaniu jest na tyle mało, że autor pamięta ich numerację i na podstawie numeru wie, o jakim równaniu pisze.

Pomysł wykorzystuje odwoływanie się do wybranej etykiety podpisu. Identyfikatorem pola SEQ może być dowolny ciąg znaków. W Wordzie podpisy pod ilustracjami, tabelkami itp. także są tworzone za pomocą pola SEQ, w którym identyfikatorem jest etykieta podpisu. Zazwyczaj jest to nazwa w rodzaju Tabela, Rysunek, ale użytkownik Worda może utworzyć także swoje własne etykiety, np. Fot.

W polskiej wersji Worda jedną z etykiet dodaną „fabrycznie” jest „Równanie”, czyli tekst identyfikatora, jaki został wykorzystany w polu SEQ podczas tworzenia mechanizmu automatycznej numeracji równań. Wykorzystując tę zgodność proponuję przy odwołaniu wskazać, jako typ odsyłacza pozycję: „Równanie”.

Na liście – w sekcji: „Do którego podpisu” – pojawią się numery równań. Przykład widoczny jest poniżej.

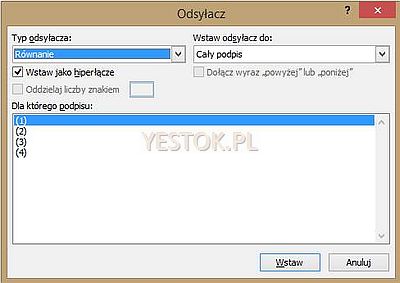
Przy tym sposobie wykorzystywania odsyłaczy należy pamiętać, że identyfikator pola SEQ wpisywany przez nas podczas tworzenia automatycznej numeracji równań (pkt. 11 procedury) musi być dokładnie taki sam jak etykieta podpisu. Ten zapis jest wrażliwy na wielkość liter.