Yestok.pl

Ktoś kiedyś powiedział, że dobrze przygotowane zestawienie tabelaryczne jest o wiele lepsze niż kilka stron opisu. Ktoś inny uzupełnił to zdaniem, że dobra prezentacja graficzna wyników to sto razy lepsze niż tabelka. Sam się o tym przekonałem, kiedy prezentowałem zagadnienie kosztów produkcji wyrobów fabryki, w której wówczas pracowałem, w opozycji do działu kosztów, który wszystko przygotował w postaci zestawień tabelarycznych.

Podstawą takiej graficznej prezentacji są wykresy. Te z kolei są graficzną reprezentacją zgromadzonych danych, pewną aproksymacją tych danych lub odzwierciedleniem zależności zachodzących między danymi.

Dodanie wykresu do opracowanego tekstu często ułatwia jego zrozumienie lub unaocznia opisywane procesy a dodatkowo uatrakcyjnia samo opracowanie. Przygotowanie właściwego wykresu jest więc cenną umiejętnością. Zobrazowaniem tego opisu niech będzie poniższy rysunek. Górną jego część stanowi pewne zestawienie tabelaryczne, dolną – to samo zestawienie przedstawione w postaci wykresu kolumnowego.

Wykresy zawsze opierają się o pewne tabelaryczne zestawienia. A skoro programy biurowe mają możliwość prezentowania danych tabelarycznych, to kwestią czasu było pojawienie się możliwości automatycznego tworzenia wykresów na podstawie tych danych. Zestawienia mogą być tworzone w edytorach tekstowych, takich jak Word czy Writer, w arkuszach kalkulacyjnych, odpowiednio Excel lub Calc, lub w innych dedykowanych programach. W omawianym w serwisie oprogramowaniu Google Docs („Arkusz kalkulacyjny dla absolutnie zielonych”), wykresy można przygotować tylko w arkuszu kalkulacyjnym. Programy edytorskie oraz kalkulacyjne mają wbudowaną możliwość tworzenia wykresów na podstawie zgromadzonych danych. Najlepiej i najwcześniej zagadnienie to zostało rozwiązane w przypadku arkuszy kalkulacyjnych. Skromniejsze możliwości miały edytory tekstów, jednak obecnie rozwiązano ten problem poprzez powiązanie wykresu z tabelą znajdującą się w dokumencie na poziomie procedur wspólnych dla edytorów i arkuszy kalkulacyjnych. Tabela taka może być rozbudowywana i przeredagowywana przez edytor tekstowy (tak jest w edytorze Writer) albo przez wywołanie w tle programu arkusza kalkulacyjnego (tak jest w edytorze Word, który uaktywnia program Excel do obsługi tabeli). Opracowanie to napisałem z myślą o ogólnej wiedzy na temat wykresów. Jakie są ich typy? W jaki sposób agregować dane? Jak odnieść je do rzeczywistych obserwacji? Dlatego nie poruszam tu szczegółów, jak tworzyć wykres. Zazwyczaj metoda zależy od konkretnego programu. Z reguły wystarczy wybrać pozycję menu odpowiedzialną za wykresy a programy „same” poprowadzą nas za rękę pytając o typ wykresu, wariant i dane do jego utworzenia. Przygotowując jednak ten rodzaj grafiki warto wiedzieć, jakie te wykresy są, jak je interpretować i jak przygotować dane. Temu ma służyć to opracowanie.

Pierwszą, prymitywną metodą graficznej interpretacji wyników, było wprowadzenie do arkusza kalkulacyjnego formatu liczbowego „*” (gwiazdka). Format ten powodował wyświetlenie w komórce tylu gwiazdek, ile wynosiła liczba wpisana do komórki. Jeśli komórki z tym formatem umieszczono jedna pod drugą, to w efekcie można było otrzymać coś w rodzaju wykresu słupkowego. Ograniczeniem była szerokość komórki, która pozwalała wyświetlić tylko pewną skończoną liczbę znaków. W programie VisiCalc maksymalna szerokość komórki wynosiła 39 znaków, w Lotusie 1-2-3 już 240 znaków. W wersji 2.4 programu Lotus 1-2-3 format ten rozwinięto do postaci, w której znaki „+” (plus) prezentowały wartości dodatnie, znaki „-” (minus) wartości ujemne a wartościom 0 (zero) odpowiadał znak separatora dziesiętnego liczby. Przykład takiego „wykresu” przygotowanego w arkuszu kalkulacyjnym Lotus 1-2-3 pokazuję na rys. 2.

Oczywiste jest, że rzadko zdarza się by rejestrowane wartości zawierały się w przedziale od 0 do 240. Widać to na powyższej ilustracji, która obrazuje pewne otrzymane wyniki dla dziesięciu kolejnych miesięcy roku. „Wykres” chcę przedstawić w komórkach o szerokości około 40 znaków. Dlatego najpierw przygotuję przeliczone wartości, odpowiadające tym rzeczywistym, ale pozwalające przedstawić je na „wykresie”. Założyłem, że bazą wykresu będzie wartość 3500, czyli „wykres” będzie prezentował wartości większe od tej liczby. Obliczyłem wartość minimalną w zbiorze liczb (komórka A13), wartość maksymalną w tym zbiorze (komórka A14) oraz różnicę między tymi wartościami (komórka A15). Założyłem też, że „dynamikę wykresu” przedstawię na 37 znakach. Dlatego uzyskaną różnicę podzieliłem przez 37, wynik widoczny jest w komórce A16. Oznacza on, że każdej wielokrotności liczby 158,4 odpowiadać będzie odpowiednia krotność znaków „+”. Teraz w komórkach kolumny D wpisałem formuły, treść takiej formuły wpisanej do komórki D2 to „(B2-3500)/$A$16”. Pozostałe komórki tej kolumny zawierają formuły o analogicznej budowie, powiązane z odpowiednimi komórkami w kolumnie „B”. Formuła oblicza ile przedziałów, po 158,4, mieści się w obliczanej różnicy. Przypisanie komórkom kolumny „D” formatu „+/-” (bo taką nazwę nosi ten zmodyfikowany format gwiazdkowy w Lotusie), spowodowało wyświetlenie odpowiedniej liczby znaków „+”.

Tak właśnie można było przygotować pierwsze graficzne prezentacje odnoszące się do zgromadzonych danych w arkuszach kalkulacyjnych, dostępnych pod koniec XX wieku.

Przejście systemów komputerowych ze środowiska znakowego do świata graficznego, całkowicie odmieniło rolę, postrzeganie i możliwości prezentowania danych. Przede wszystkim wykres stał się oddzielnym obiektem osadzonym w dokumencie. Odpowiednie algorytmy tworzą wykres na podstawie danych znajdujących się w innym miejscu a sam wykres może przedstawiać jednocześnie kilka różnych danych (nazywanych seriami danych) i dopasowywać się do wymiarów narzuconych przez użytkownika. Zasada tworzenia wykresów pozostała jednak taka sama. Różnica między największą i najmniejszą wartością musi zostać przedstawiona na pewnej odległości, tym razem wyrażonej w pikselach, czyli najmniejszych, samodzielnie świecących punktach ekranu.

Dane do wykresu są zorganizowane w postaci tabeli o zróżnicowanej liczbie wierszy i kolumn. Serie danych, czyli wartości cech, są zapisywane kolumnami, a nazwa cechy jest zapisana w nagłówku odpowiedniej kolumny. Wartości cech odpowiadają wartościom osi „Y” na wykresie. Wiersze tabeli odpowiadają węzłom wykresu, dla których te cechy zostały zmierzone. Nazwa węzła znajduje się w boczku wiersza. Użyłem tu określenia „węzeł”, gdyż nie zawsze jest to wartość liczbowa odnotowywana na osi „X”. Zademonstrowane przykłady wyjaśnią, o co chodzi. Możliwość prezentowania na ekranie dowolnych kształtów pozwoliła zaprojektować wiele, bardzo interesujących pod względem wizualizacji, typów wykresów. Jak wspomniałem wykres może prezentować jednocześnie kilka różnych cech, czyli serii danych.

W tym opracowaniu postaram się omówić podstawowe, najczęściej spotykane typy.

Pierwszym omawianym typem jest wykres słupkowy. Jest on bezpośrednim następcą pokazanego powyżej wykresu gwiazdkowego. Obecnie jest rzadziej spotykany, gdyż jego postrzeganie wydaje się mniej skuteczne od odpowiadającego mu wykresu kolumnowego. Cechą tego wykresu jest umieszczenie węzłów na osi pionowej a wartości prezentowanych serii danych, na osi poziomej.

Przykład takiego wykresu wraz z seriami dotyczących go danych przedstawia rys. 3.

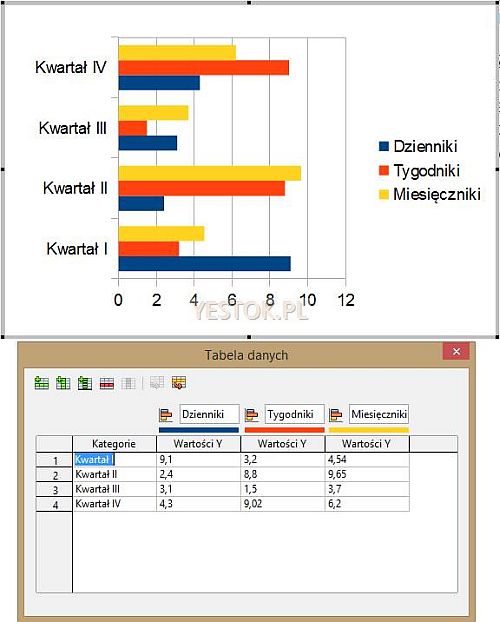
Węzłami na tym wykresie są nazwy kolejnych kwartałów a seriami danych – sprzedaż w tych kwartałach wybranych typów czasopism. Dane wykresu tego nie precyzują, ale mogą to być łączne nakłady w milionach sztuk, wartość sprzedaży w milionach złotych czy ilość wyciętego – na potrzeby druku tych czasopism – lasu, w tysiącach hektarów.

Drugim typem wykresów są wykresy kolumnowe. Jest to chyba najczęściej wykorzystywany typ wykresów. W gruncie rzeczy odpowiada on obróconemu o 90 stopni wykresowi słupkowemu. Oś pozioma odpowiada węzłom wykresu a oś pionowa wartościom przypisanym cechom. Poniżej znajduje się wykres kolumnowy dla tych samych danych, jakie wykorzystałem w wykresie słupkowym.

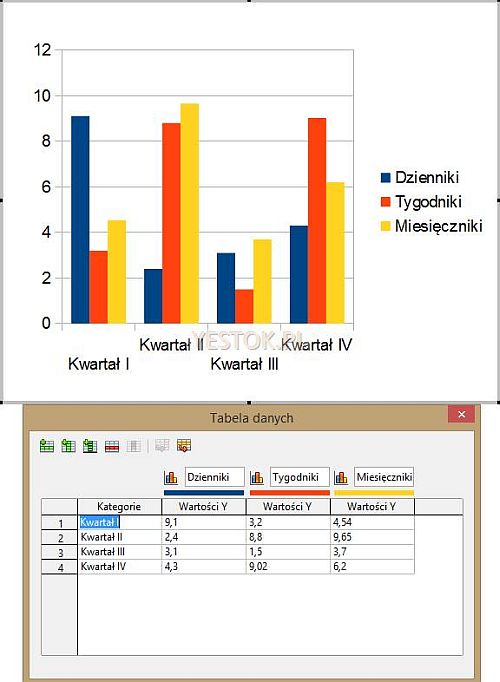
Wykresy słupkowe i kolumnowe mogą być przedstawiane w dwóch dodatkowych wariantach. Pierwszy z nich to tak zwany wykres skumulowany, prezentujący dla każdego węzła sumaryczną wartość cech z wyróżnieniem każdej z nich w tej sumie. Postać takiego wykresu dla wartości takich samych jak na rys. 4, już bez tabeli danych, przedstawia rys. 5.

Oczywiście kumulowanie wartości ma sens tylko wtedy gdy rejestrowane cechy są tego samego rodzaju. Trudno byłoby wyobrazić sobie wymowę takiego wykresu, choć można go sporządzić, jeśli rejestrowanymi cechami byłyby np. liczba zatrudnionych, nakład i wartość sprzedaży.

I drugi wariant, to wykres nazywany we Writerze i Calcu jako „procentowy”, w Wordzie i Excelu jako „100% skumulowany”. Ten wykres także kumuluje wszystkie wartości cech dla węzła, ale sumaryczną wartość każdego węzła traktuje jako 100% i wartości poszczególnych składowych przedstawia jako odpowiedni udział w tej stuprocentowej wartości. Uwaga o jednorodności cech jest także zasadna w przypadku tego wykresu. Przykład takiego wykresu, dla tych samych danych co powyżej przedstawia rys. 6.

W tym wykresie wszystkie kolumny są takiej samej wysokości, gdyż każda z nich prezentuje 100%. Wykres nie mówi więc nam o bezwzględnej wielkości wyników, ale pozwala unaocznić strukturę każdego węzła.

Wykresy kolumnowe i słupkowe mogą mieć jeszcze inne dodatkowe cechy, niewynikające jednak z prezentowanych danych, lecz ich graficznej prezentacji. Tymi efektami są zróżnicowane pod względem kształtów wyobrażenia trójwymiarowe. Dane przedstawiane są więc jako graniastosłupy, walce, ostrosłupy lub stożki. Przykład takich wykresów przedstawia ilustracja poniżej.

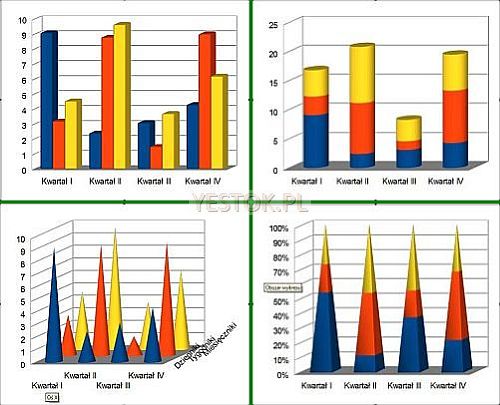
Wykorzystanie takich zróżnicowanych wykresów ma jednak bardziej charakter estetyczny niż merytoryczny.

Bardzo popularnym typem wykresu jest wykres kołowy i dodany nieco później wykres pierścieniowy. Wykres kołowy dotyczy zawsze tylko jednej serii danych. Dane te przedstawione są w postaci wycinka koła odpowiadającego procentowemu udziałowi tego wycinka w całym kole. Przykładowy wykres także oparty jest o dane w pokazanej już tabeli.

Mimo że tabela danych zawiera trzy kolumny wartości, do utworzenia wykresu wybrana zostanie tylko jedna kolumna. W pokazanym przypadku jest to kolumna druga, przylegająca do opisu węzłów, ale w niektórych programach można wskazać, która kolumna ma być podstawą tworzonego wykresu.

Swoistym wariantem wykresu kołowego jest wykres pierścieniowy. Może on prezentować dane kilku serii. Każda z tych serii przedstawiana jest w postaci pierścienia, którego wycinki odpowiadają udziałowi w swojej serii danych. Tworząc wykresy kołowe i pierścieniowe można przedstawiać je jako elementy rozdzielone lub wydzielić – „wysunąć” – tylko jeden element z całości. Kilka takich przykładów przedstawia ilustracja poniżej.

W dotychczas przedstawionych typach wykresów ich węzłami mogły być w zasadzie dowolne kategorie. Przykład wykorzystany przeze mnie obejmował kolejne kwartały sugerując pewne następstwo węzłów. Ale tego typu wykresy, jako węzły, mogą mieć podane dowolne elementy. Mogłyby to być np. nazwy warzyw jak np. marchew, kapusta, seler i brokuł, natomiast serie danych dotyczyć składników odżywczych, w rodzaju: węglowodany, proteiny, laktoza, cukry itp. W takich wykresach kolejność wpisanych węzłów nie ma znaczenia.

Jeśli jednak oś pozioma wykresu powinna być uporządkowana w kolejności rosnącej lub malejącej, do wykorzystania są inne typy wykresów. Jednym z nich jest wykres liniowy.

Jest wygodnym typem do prezentowania trendu zdarzeń zachodzących w równych odstępach czasowych. Zarówno dla zdarzeń rejestrowanych co sekundę, jak i dla zdarzeń rejestrowanych co wiek.

Poniżej na ilustracji wymyślony przykład sprzedaży trzech tytułów prasowych w poszczególnych dniach tygodnia.

Wykresy liniowe także mają swoje warianty. Można przedstawić w nich tylko punkty odpowiadające wartościom, połączyć ukryte punkty wygładzonymi liniami albo przedstawić wartości w przestrzeni trójwymiarowej. Także i ten typ wykresów można przedstawiać jako wykresy skumulowane. Te właśnie przypadki, tego samego wykresu, jaki pokazałem na rys. 11., przedstawiam na kolejnej ilustracji.

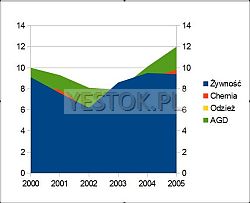
Podobnym typem do wykresu liniowego jest typ warstwowy. On także dobrze nadaje się do prezentowania trendów w rejestrowanych zjawiskach. Jednak jego właściwości najlepiej predysponują go do wariantu wykresu skumulowanego. Serie danych prezentowane są bowiem jako powierzchnie zawarte między osią poziomą a linią wyznaczającą wartości serii, wypełnione kolorem różnym dla każdej serii. Ten typ wykresu może być słabo czytelny w swojej podstawowej postaci. Ilustracja 13. przedstawia skumulowaną sprzedaż supermarketu w ciągu kilku lat z podziałem na artykułu żywnościowe, chemię, odzież i AGD.

Poniżej przedstawiam trzy inne warianty wykresu warstwowego dla tych samych danych. Wariant zwykły – trzecia z ilustracji – jest jak widać słabo czytelny ze względu na przykrywanie wartości mniejszych wartościami większymi. Pozostawiłem wykres w takiej postaci, chociaż autor opracowania może tak zmodyfikować kolejność serii danych aby wszystkie dane były widoczne, by pokazać także pułapki czyhające na przygotowującego opracowanie. Pozostałe dwie ilustracje przedstawiają wykres trójwymiarowy i wykres procentowy.

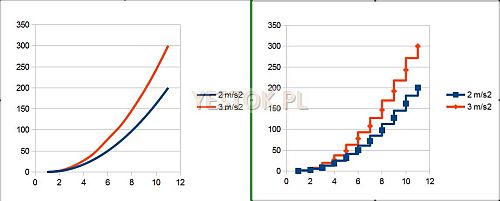
Kolejnym typem wykresów jest typ punktowy. Ten typ przedstawia relację par wartości, z których jedna jest wartością niezależną. Wykres może zawierać kilka serii danych, jednak odpowiadające sobie wartości tych serii są zawsze „sparowane” z jedną wartością niezależną. Serie wartości muszą być uszeregowane zgodnie z posortowaną kolejnością wartości niezależnych. Wiele algorytmów przygotowujących takie wykresy wykonuje takie sortowanie automatycznie. Tego rodzaju wykresy najbardziej nadają się do prezentacji badań naukowych, szczególnie w dziedzinie nauk ścisłych. W tego typu wykresach oś pozioma jest typową, liczbową osią „X”. Jako przykład pokażę wykres obrazujący drogę przebytą przez obiekty poruszające się ruchem jednostajnie przyspieszonym, jeden z przyspieszeniem 2 m/s², drugi – 3 m/s². Oś pozioma reprezentuje wartości niezależne, w tym przypadku czas w sekundach. Oś „Y” przedstawia drogę przebytą w metrach.

Wykres powyżej przedstawia zarejestrowane pary wartości w postaci znaczników, lecz wśród dostępnych wariantów wykresu punktowego znaleźć można m.in. wygładzony wykres liniowy z ukrytymi punktami danych albo wykres schodkowy. W przypadku prezentacji tego akurat zagadnienia – wariant taki jest niezbyt przydatny. Umieściłem go jednak na ilustracji by i taki pokazać.

Wykresy liniowe, warstwowe, punktowe a formalnie także kolumnowe i słupkowe mogą zawierać naniesione dodatkowe linie, generowane przez procedury tworzenia wykresów. Linie te wynikają ze zgromadzonych danych. Takimi liniami mogą być linie średniej, krzywe regresji lub słupki błędów.

Rodzaj i możliwość umieszczenia tych elementów zależy od konkretnych rozwiązań programowych. W powszechnie stosowanym arkuszu kalkulacyjnym Excel i odpowiadającym mu arkuszu kalkulacyjnym Calc możliwości te są zróżnicowane, chociaż w obu tych programach nanieść można krzywe regresji i słupki błędów. Wykorzystanie tych możliwości wymaga jednak od autora wiedzy na temat statystyki i umiejętności interpretacji wyników.

Krzywa regresji, zwana też linią trendu, to linia odpowiadająca pewnej funkcji, wyznaczonej na podstawie zarejestrowanych danych. Funkcja ta ma jak najlepiej opisywać matematyczną zależność między zmienną niezależną (x) a zmienną zależną (y). Dzięki poznaniu tej funkcji można oszacować oczekiwaną wartość zmiennej y w punktach x, nierejestrowanych w badaniach.

Słupki błędów pozwalają nanieść na zarejestrowane punkty wykresu pewnego interwału obrazującego możliwe błędy wyników.

Przykładem takiego wykresu jest wykres pokazany poniżej. Dla zmiennej reprezentowanej przez niebieskie prostokąty wyznaczyłem krzywą regresji typu potęgowego. Funkcja ta da się opisać wzorem umieszczonym na wykresie. Znak „^” w tym wzorze oznacza potęgowanie.

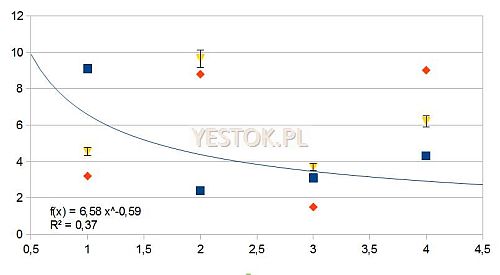
Na wykresie znalazł się też obliczony dla tych danych współczynnik R² (determinacji).

Położenie punktów serii oznaczonej żółtymi trójkątami zostało uzupełnione o słupki błędów wynoszące 5% każdej wartości. Dlatego interwał przy wartości w pobliżu dziesięć jest większy niż w pobliżu wartości cztery. Słupki błędów mogą mieć wartość stałą, procentową, odpowiadać wartości błędu standardowego, odchylenia standardowego lub inną, wynikającą z używanego programu.

Wykres radarowy (w terminologii Microsoft) albo siatkowy (w terminologii (x)Office). Określenie „radarowy” odwołuje się do znanego z filmów i gier, ekranu radaru. Ten bardzo ciekawy wykres zawiera tyle osi ile zdefiniowano w tabeli węzłów a wszystkie osie rozpoczynają się w punkcie centralnym. Sposób prezentacji pozwala ocenić rozprzestrzenianie się rejestrowanych zjawisk w ramach węzłów. Przykład poniżej przedstawia wymyślony procent czytelników trzech dzienników w okresie od stycznia do maja.

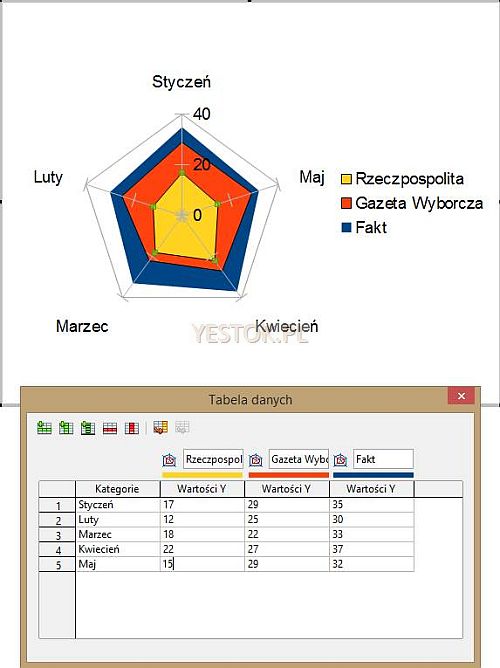
Z wykresu łatwo wywnioskować, że najbardziej poczytnym dziennikiem w całym tym okresie był „Fakt”.

Inne warianty tego typu wykresu przedstawiam poniżej.

Wykresem, który może zawierać wiele serii danych jest także wykres kolumnowo-liniowy. Jest to wykres, w którym wybrane serie danych przedstawione są za pomocą kolumn a pozostałe – linii. Ten typ wykresu ma także wariant ze skumulowanymi kolumnami. Serie danych prezentowane przez linie nie są wówczas kumulowane. Przykład takiego wykresu przedstawia rys. 20.

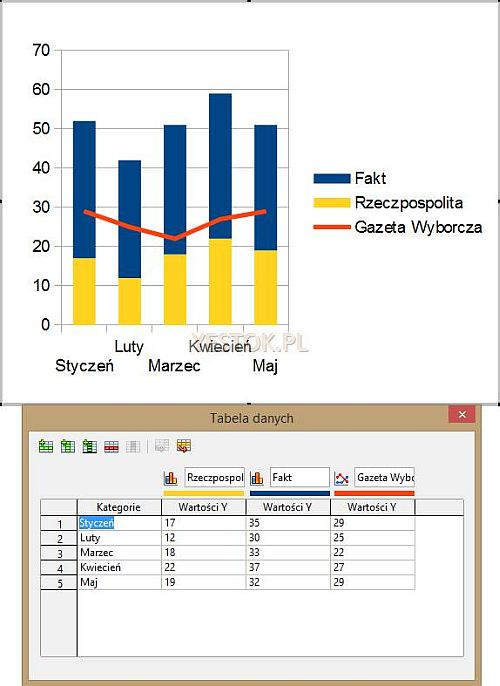
Typy wykresów omówione powyżej pozwalają na jednym wykresie odzwierciedlać zależności dotyczące kilku serii danych. Jedynie wykres kołowy związany jest z jedną tylko serią. Dostępne są jednak także typy wykresów, w których serie danych to w rzeczywistości kilka podzbiorów danych.

Pierwszym omawianym typem będą wykresy bąbelkowe (taką nazwę noszą w terminologii Microsoftu) albo dymkowe (tak nazywane są w oprogramowaniu (x)Office).

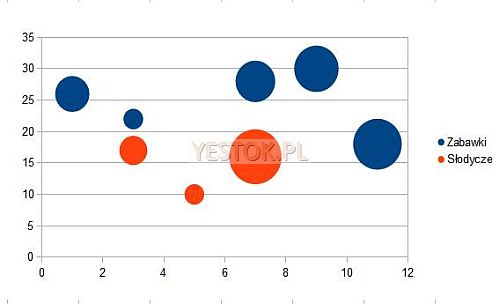
Wykresy te w istocie są podobne do wykresów punktowych. Kolumnie danych niezależnych odpowiadają jednak dwie związane ze sobą kolumny danych zależnych. Kolejna seria danych to dwie kolejne kolumny związanych ze sobą danych. Wartość zmiennej niezależnej i pierwszej wartości serii danych odpowiada położeniu punktu w obszarze wykresu względem osi „X” i „Y” tak jak w wykresie punktowym. Druga wartość w tej serii danych decyduje o fizycznej wielkości tego punktu. Ponieważ punkty te pokazywane są zazwyczaj jako kolorowe kółka i ze względu na różne rozmiary przypominają jednym bąbelki a innym dymki, stąd nazwa tego typu wykresu.

Przykład takiego wykresu przedstawia rysunek 21.

Przedstawiony wykres analizuje firmy kurierskie i prezentuje jedną serię danych. Dane są oczywiście całkowicie fikcyjne. Oś „X” wykresu pokazuje liczbę posiadanych samochodów. Oś „Y” obrazuje tonaż przewiezionych przesyłek. Druga wartość tej serii, która jednocześnie decyduje o wielkości bąbelka, odpowiada przychodom firm z tytułu świadczonych usług (np. w milionach złotych). Oprogramowanie generujące wykres samodzielnie porządkuje oś „X” w kolejności wzrastającej wielkości oraz dobiera wielkość bąbelków na podstawie wartości występujących w kolumnie odpowiadającej za ich wielkość.

Wykres ten może zawierać kolejne serie danych. Każda z nich musi składać się z par wartości. Wartości odpowiadającej za oś „Y” i za wielkość bąbelka. Wartości osi „X” są wspólne dla wszystkich serii. Gdy wartości osi „X” nie odpowiada żadna para liczb serii albo nie ma jednej z liczb w parze, miejsce takie na wykresie pozostaje puste.

Przykład wykresu bąbelkowego, zawierające dwie serie danych pokazuje rys. 22. Na wykresie widać, że nie wszystkie pary obu serii pokrywają się wzajemnie.

Typem, o jakim chcę jeszcze powiedzieć to wykresy giełdowe. Są to wykresy wyspecjalizowane pod kątem pracy analityków giełdowych. W swojej standardowej postaci wymagają zgromadzenia dla każdego węzła serii danych składających się z trzech wartości. Przez serię rozumieć należy w tym przypadku nazwę spółki. Te dane to: kurs minimalny, kurs maksymalny i kurs zamknięcia. W wariantach tego wykresu można uwzględniać dodatkowo także kurs otwarcia i wartościowy lub ilościowy wolumen obrotów.

Wykres może wyświetlać dane o wielu spółkach. W powyższym przykładzie zgromadzono informacje o notowaniach z pierwszych 10. dni w miesiącu jednej spółki, KGHM. Słupek dla każdego dnia przedstawia rozstęp między minimalną a maksymalną ceną akcji w dniu notowań oraz cenę w momencie zamknięcia notowań (to ten mały występ przy każdym słupku). Inny z wariantów może pokazywać także zysk lub stratę na akcjach, uwzględniając w obliczeniach ceny otwarcia i zamknięcia. Przykład takiego wariantu poniżej.

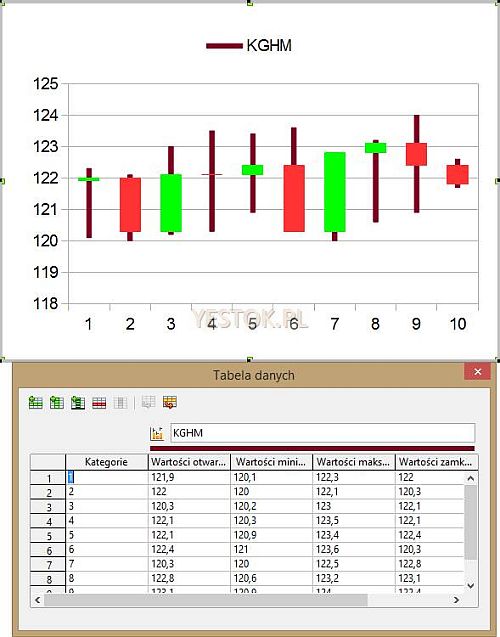
Aby uzyskać taki wariant seria danych musi składać się z czterech wartości. Dodatkowo musi wystąpić także kurs otwarcia. Na podstawie danych, procedury tworzenia wykresu obliczyły różnice między wartością otwarcia i zamknięcia, przedstawiając zysk kolorem zielonym a stratę kolorem czerwonym.

Przedstawione w opracowaniu typy wykresów należą do powszechnie stosowanych. Wiele programów udostępnia jednak dodatkowe, niespotykane w innych rozwiązaniach typy wykresów. Najczęściej są one dostępne w programach arkuszy kalkulacyjnych lub innych, dedykowanych do tworzenia wykresów. Mogą to być np. wykresy zintegrowane z mapami albo wykresy powierzchniowe odzwierciedlające zależności funkcyjne od dwóch zmiennych.

Zasada jest zawsze taka sama. Należy w odpowiedni sposób zorganizować dane niezbędne do utworzenia wykresu i zawsze dane te są zorganizowane w postaci tabel. Użytkownik może ingerować w tworzenie wykresu. Może decydować o kolorach, liniach, kształtach, opisach osi, zawartości i położeniu legendy, tytułu i podtytułu wykresu. O zastosowanej podziałce lub drugiej inaczej wyskalowanej osi. Metody „obsługi” wykresu w tym zakresie mogą różnić się w zależności od używanego programu, dlatego nie są omawiane w tym opracowaniu. Jako ostatnią, ilustrację przedstawiam przykładowy wykres, wskazując na nim prawie wszystkie elementy, na które ma wpływ autor.

Gromadząc dane do tworzonego wykresu należy pamiętać, że nie każdy utworzony wykres może być czytelny i adekwatny do sytuacji. Jeśli w przygotowywanym wykresie jedna lub kilka wartości znacznie odbiega od rejestrowanych w serii, wykres może być całkowicie nieczytelny, gdyż aby przedstawić na wykresie wartości największe, te niewielkie mogą nawet nie być widoczne. Łatwo wyobrazić sobie jak może wyglądać wykres przedstawiający temperatury topnienia różnych pierwiastków, na którym dla porównania umieszczono także temperaturę panującą na powierzchni słońca.

Do utworzenia prawie wszystkich prezentowanych przykładów wykorzystałem program Writer. Dołączone tabele danych pokazują sposób organizacji danych.

Sposób tworzenia wykresu w środowisku programu Writer, oprogramowania Apache OpenOffice i LibreOffice, opisałem w odrębnym opracowaniu. Można je przeczytać przechodząc do strony „Writer a wykresy w dokumentach”.

Sposób tworzenia wykresu w środowisku programu Word opisałem w odrębnym opracowaniu. Można je przeczytać przechodząc do strony Tworzenie wykresów w programie Word.